Deep Double Descent Where Bigger Models and More Data Hurt: Difference between revisions
| Line 24: | Line 24: | ||
The below is the formal definition of Effective Model Complexity: | The below is the formal definition of Effective Model Complexity: | ||
[[File:definition.png]] | [[File:definition.png| 800px]] | ||
== Model Architectures and Experiments == | == Model Architectures and Experiments == | ||
Revision as of 11:53, 20 November 2021
Work In Progress. Delete this sentence when finished.
Presented By
Sam Senko, Tyler Verhaar and Ben Zhang
Introduction (Ben)
In classical statistical learning theory, the bias-variance trade-off is a fundamental concept. The idea is that higher complexity models have lower bias but higher variance. Based on this idea, concepts like overfitting and under-fitting are introduced to classification model training process. However, the paper presents the modern theories that could overthrow the "conventional wisdoms" mentioned above.
Though with millions of parameters, complex models which generally performs much better than simpler models, behaves differently from what conventional concepts indicate. Two regimes in deep learning are introduced in this paper. In under-parameterized regime, where the model has lower complexity has the "U" shape bias-variance trade off for the test error. This regime represents the conventional idea. However, once the model has sufficiently large complexity to interpolate (- training error), then modern tuition as this paper suggests "bigger models are better".
Previous Work (Ben)
Belkin er al. (2019) who first postulated in generality the phenomenon that "bigger models are better" named it "double descent" and demonstrated this phenomenon for Decision Trees, Random Features, and 2-layer Neural Networks with l2 loss on a variety of learning task including MNIST and CIFAR-10.
However, similar behaviour had been observed in Opper (1995; 2001), Advani & Saxe (2017), Spigler et al. (2018) and Geiger et al. (2019b). This concept has then been applied to various field including identity mapping in Computer Vision Deep Residual Networks by Kaiming He, Xiangyu Zhang, Shaoqing Ren and Jian Sun, explaining and harnessing adversarial examples by Ian J Goodfellow, Jonathon Shlens and Christian Szegedy.
Motivation (Ben)
Since traditional notion of model complexity has not captured the model's performance well, the notion of "Effective Model Complexity" were introduced in this paper to fill the gap.
We define the training procedure T to be any procedure that takes input set S = {(x1,y1),...., (xn,yn)} of labeled training samples and output a classifier T(S) that maps data to labels to perform classification tasks. We define Effective Model Complexity of T (with respect to distribution) to be the maximum number of samples n on which T achieves on average approximately 0 training error.
The below is the formal definition of Effective Model Complexity:
Model Architectures and Experiments
A variety of experiments were done to demonstrate the double descent phenomenon and its connection to effective model complexity in a number of different situations. Three main model architectures were used in these experiments:
- A simple convolutional neural network with 4 convolutional layers and 1 fully connected layer. The widths of the convolutional layers were k, 2k, 4k and 8k respectively where k is a parameter which was varied in the experiments.
- Resnets, introduced in (He, et al., 2016), with the convolutional layers having widths k, 2k, 4k and 8k respectively where k is again a parameter
- Transformers, a type of recurrent neural network often used in natural language processing. This used a 6-layer architecture. The embedding dimension was varied to vary the complexity of the model and the width of the fully connected layers was scaled proportionately to this embedding dimension.
The above models were trained with variants of gradient descent, with the number of gradient steps varying from around 5 thousand to around 500 thousand depending on the particular model and the experiment. In some experiments, label noise was used where, with probability p, the label was replaced by an incorrect label chosen uniformly at random.
The first experiment investigated the effect of varying model complexity at various levels of label noise. Results are given below:
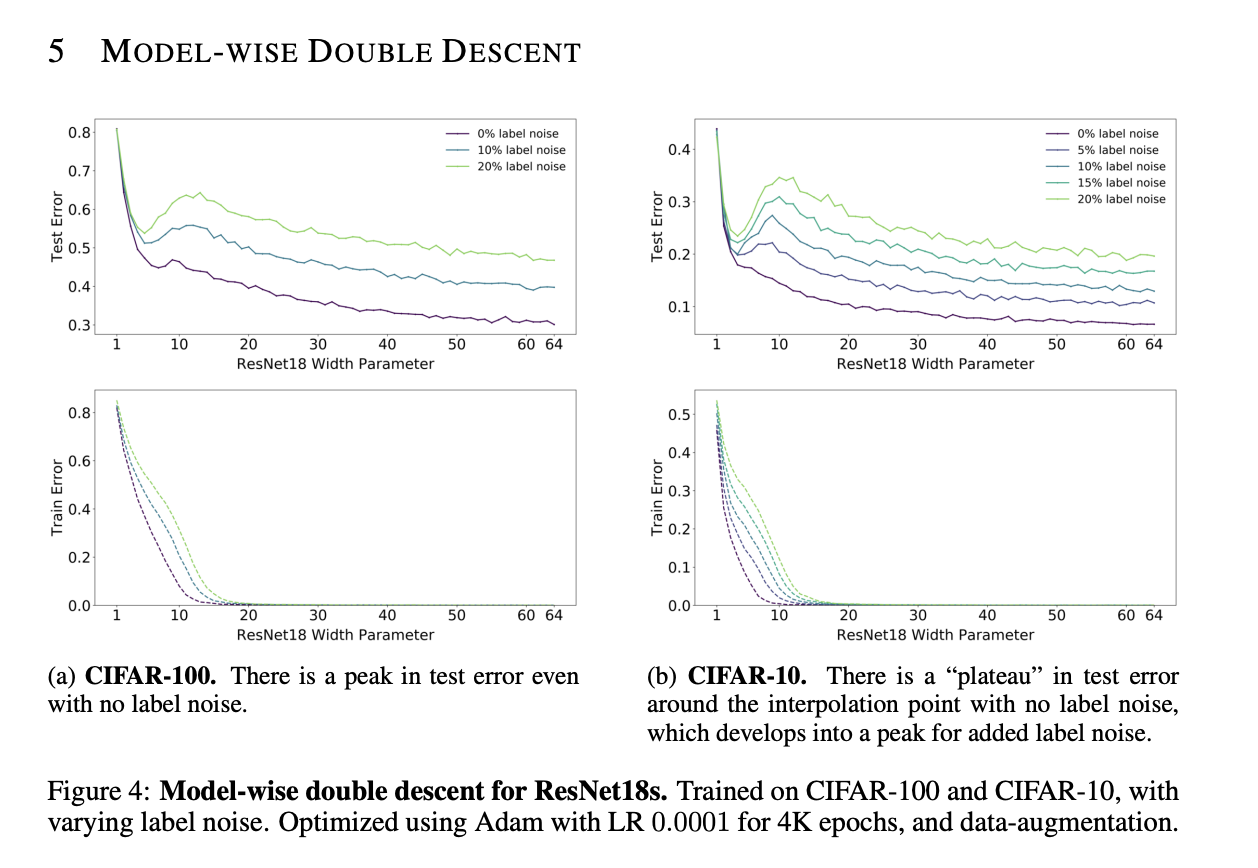 A few observations can be made, confirming the predictions of the paper authors. Firstly, there is double descent, with the test error decreasing until a certain point at which the model overfits leading to an increase in test error followed eventually by a second decrease in the test error. Additionally, at all levels of label noise, the peak occured around the threshold where the EMC is approximately the size of the dataset (and so the train error first approaches 0), confirming the hypotheses made by the authors. Finally, increasing label noise naturally moved this critical threshold further right which can be seen by the peaks being further right with more label noise.
A few observations can be made, confirming the predictions of the paper authors. Firstly, there is double descent, with the test error decreasing until a certain point at which the model overfits leading to an increase in test error followed eventually by a second decrease in the test error. Additionally, at all levels of label noise, the peak occured around the threshold where the EMC is approximately the size of the dataset (and so the train error first approaches 0), confirming the hypotheses made by the authors. Finally, increasing label noise naturally moved this critical threshold further right which can be seen by the peaks being further right with more label noise.
The next experiment investigated the effect of the number of epochs used on the test error for a variety of different model complexities. Note that increasing the number of epochs increases the EMC, although it may be impossible to reach a particular EMC without also increasing the model complexity.
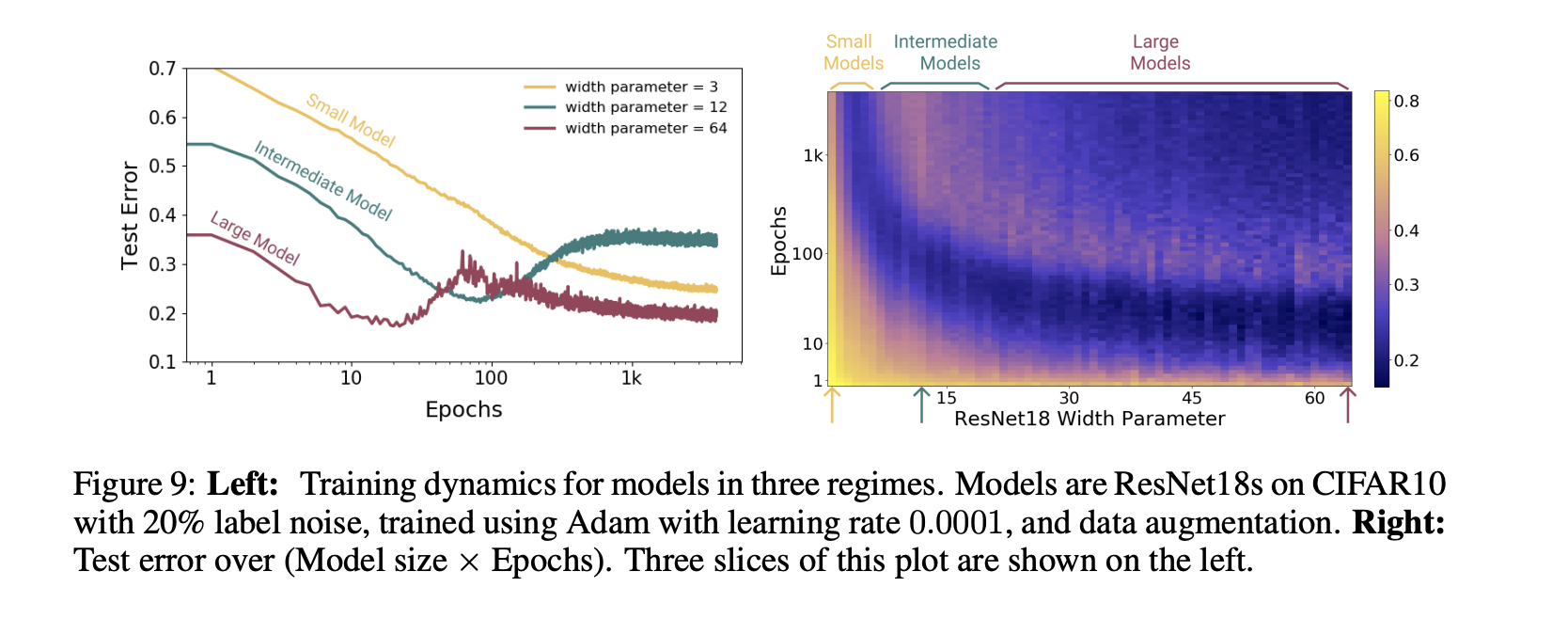 Here, we see that the small model is unable to reach a sufficiently large EMC to see overfitting begin. For the medium-sized model, the model is just barely able to reach an EMC of approximately the size of the data and, therefore, sees a traditional U-shaped curve without a further decrease in the test error. However, the large model, which is able to exceed the threshold where EMC is approximately the data size, does see a double descent as would be expected. This has the practical implication that certain forms of early stopping may not be effective for very large models, as they may stop before reaching the second descent.
Here, we see that the small model is unable to reach a sufficiently large EMC to see overfitting begin. For the medium-sized model, the model is just barely able to reach an EMC of approximately the size of the data and, therefore, sees a traditional U-shaped curve without a further decrease in the test error. However, the large model, which is able to exceed the threshold where EMC is approximately the data size, does see a double descent as would be expected. This has the practical implication that certain forms of early stopping may not be effective for very large models, as they may stop before reaching the second descent.
The last experiment looked at how test error changes with varying sizes of the data used to train the model. Note that as the data size is increased, the interpolation threshold (that is, the model complexity needed to achieve near-zero train error) increases. The results of this experiment are in the next figure:
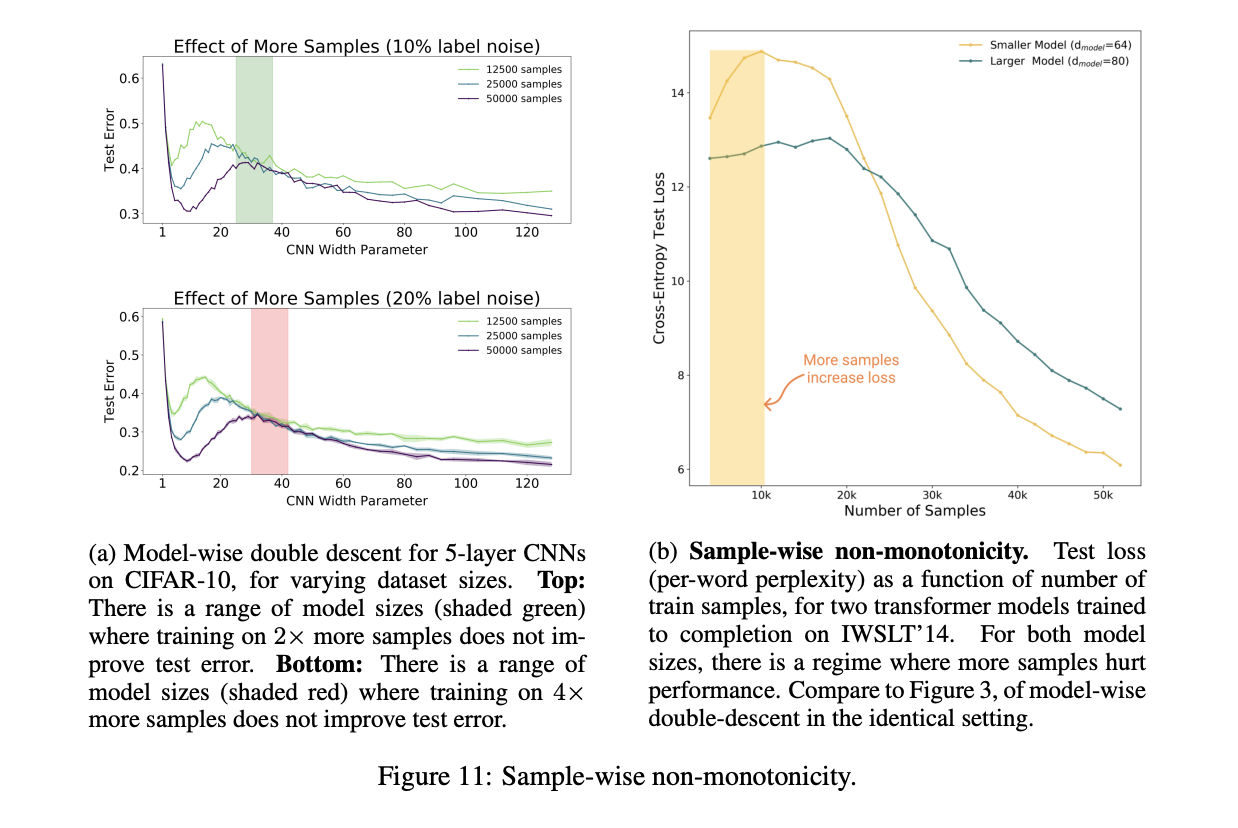 As expected, the total area under the test error curve decreased as the size of the dataset used increased (meaning that, overall, more data was generally better). However, corresponding to the rightward shift in the interpolation threshold, the peak of the test error curve also shifted to the right as more data was used. This had the perhaps unexpected effect that, at certain complexity levels, the model which was trained on more data performed similarly to or in some cases even worse than the model trained on less data. Note that all of these results do agree with the hypotheses the authors made.
As expected, the total area under the test error curve decreased as the size of the dataset used increased (meaning that, overall, more data was generally better). However, corresponding to the rightward shift in the interpolation threshold, the peak of the test error curve also shifted to the right as more data was used. This had the perhaps unexpected effect that, at certain complexity levels, the model which was trained on more data performed similarly to or in some cases even worse than the model trained on less data. Note that all of these results do agree with the hypotheses the authors made.
