Deep Alternative Neural Network: Exploring Contexts As Early As Possible For Action Recognition
Introduction
Action recognition deals with recognizing and classifying the actions or activities done by humans or other agents in a video clip. Note that due to its pervasive nature, different domains refer to action recognition by different names like plan recognition, behavior recognition, etc. In action recognition, contexts contribute semantic clues for action recognition in video(See Fig below[8]). Conventional Neural Networks [1,2,3] and their shifted version 3D CNNs [4,5,6] have been employed in action recognition but they identify and aggregate the contexts at later stages.
The authors have come up with a strategy to identify contexts in the videos as early as possible and leverage their evolutions for action recognition. Contexts contribute semantic clues for action recognition in videos. The networks themselves involve a lot of layers, with the first layer typically having a receptive field (RF) that outputs only extra local features. As we go deeper into the layers the Receptive Fields expand and we start getting the contexts. The authors identified that increasing the number of layers will only cause additional burden in terms of handling the parameters and contexts could be obtained even in the earlier stages. The authors also cite the papers [9,10] that relate the CNNs and the visual systems of our brain, one remarkable difference being the abundant recurrent connections in our brain compared to the forward connections in the CNNs. In summary, this paper proposes a novel neural network, called deep alternative neural network (DANN), which is a based method for action recognition. The novel component is called an "alternative layer" which is composed of a volumetric convolutional layer followed by a recurrent layer. In addition, the authors also propose a new approach to select network input based on optical flow. The validity of DANN is carried out on HMDB51 and UCF101 datasets and it is observed that the proposed method achieves comparable performance against state of the art methods.
The main contributions in the paper can be summarized as follows:
- A Deep Alternative Neural Network (DANN) is proposed for action recognition.
- DANN consists of alternative volumetric convolutional and recurrent layers.
- An adaptive method to determine the temporal size of the video clip
- A volumetric pyramid pooling layer to resize the output before fully connected layers.
Related Work
There are already exists a very related paper ([11]) in the literature which proposed a similar alternation architecture. In particular, the similarity between the authors work and the aforementioned paper is that they both propose alternating CNN-RNN architectures. This similarity between the two works was noted by Reviewer 1 in the NIPS review process.
Optic Flow
Optical flow or optic flow is the pattern of apparent motion of objects, surfaces, and edges in a visual scene caused by the relative motion between an observer and a scene.
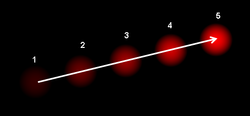
It can be used for affordance perception, the ability to discern possibilities for action within the environment. The following image describes the optical flow :
Deep Alternative Neural Network:
Adaptive Network Input
The input size of the video clip is generally determined empirically since it is hard to evaluate all the choices and various approaches have been taken in the past with a different number of frames. For instance, many previous papers suggested to used shorter intervals of between 1 to 16 frames. However, more recent work[9] recognized that human-based actions often “span tens or hundreds of frames” and longer intervals such as 60 frames will outperform the one with a shorter interval. However, there’s still no systematic way of determining the number of frames for input size of the network. This serves the motives for the authors of this paper to develop this adaptive method. Past research shows that motion energy intensity induced by human activity exhibits a regular periodicity. This signal can be approximately estimated by optical flow computation as shown in Figure 1, and is particularly suitable to address our temporal estimation due to:
- the local minima and maxima landmarks probably correspond to characteristic gesture and motion
- it is relatively robust to changes in camera viewpoint.
The authors have come up with an adaptive method to automatically select the most discriminative video fragments using the density of optical flow energy which exhibits regular periodicity. According to Wikipedia, optical flow is the pattern of apparent motion of objects, surfaces, and edges in a visual scene caused by the relative motion between an observer and a scene, and optical flow methods try to calculate the motion between two image frames which are taken at different times. The optimal flow energy of an optical field $(v_{x},v_{y})$ is defined as follows
\begin{align*} e(I)=\underset{(x,y)\in\mathbb{P}}{\operatorname{\Sigma}} ||v_{x}(x,y),v_{y}(x,y)||_{2} \end{align*}
Here, P is the pixel level set of selected interest points. They locate the local minima and maxima landmarks $\{t\}$ of $\epsilon = \{e(I_1),\dots,e(I_t)\}$ and for each two consecutive landmarks create a video fragment $s$ by extracting the frames $s = \{I_{t-1},\dots,I_t\}$.
To deal with the different length of video clip, we adopt the idea of spatial pyramid pooling (SPP) in [12] and extend to temporal domain, developing a volumetric pyramid pooling (VPP) layer to transfer video clip of arbitrary size into a universal length in the last alternative layer before fully connected layer.
Alternative Layer
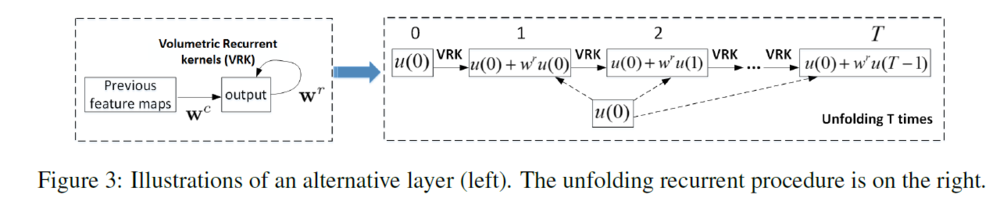
This is a key layer consisting of a standard volumetric convolutional layer followed by a designed recurrent layer. Volumetric convolutional extracts features from local spatiotemporal neighborhoods on feature maps in the previous layers and then, a recurrent layer is applied to the output and it proceeds iteratively for T times. This procedure makes each unit evolve over discrete time steps and aggregate larger RFs. The input of a unit at position (x,y,z) in the jth feature map of the ith AL in time t, $u_{ij}^{xyz}(t)$, is given by,
\begin{align*} u_{ij}^{xyz}(t) &= u_{ij}^{xyz}(0) + f(w_{ij}^{r}u_{ij}^{xyz}(t-1)) + b_{ij} \\ u_{ij}^{xyz}(0) &= f(w_{i-1}^{c}u_{(i-1)j}^{xyz}) \end{align*}
U(0): feed forward output of volumetric convolutional layer. U(t-1) : recurrent input of previous time $w_{k}^{c}$ and $w_{k}^{r}$: vectorized feed-forward kernels and recurrent kernels respectively f: ReLU function followed by a local response normalization (LRN), which mimics the lateral inhibition in the cortex where different features compete for large responses.
Figure 3 depicts this structure:
The recurrent connections in AL provide two advantages. First, they enable every unit to incorporate contexts in an arbitrarily large region in the current layer。 However, the drawback is that without top-down connections, the states of the units in the current layer cannot be influenced by the context seen by higher-level units; Second, the recurrent connections increase the network depth while keeping the number of adjustable parameters constant by weight sharing, because AL uses only extra constant parameters of a recurrent kernel size.
Volumetric Pyramid Pooling Layer
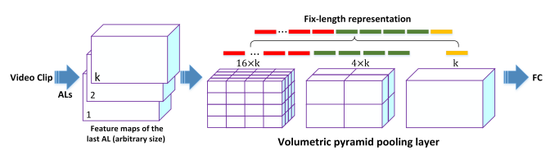
The authors have replaced the last pooling layer with a volumetric pyramid pooling layer (VPPL) as we need fixed-length vectors for the fully connected layers and the AL accepts video clips of arbitrary sizes and produces outputs of variable sizes. Figure 2 illustrates the structure of VPPL. The authors have used the max pooling to pool the responses of each kernel in each volumetric bin. The outputs are kM dimensional vectors where:
M: number of bins
K: Number of kernels in the last alternative layer.
This layer structure allows not only for arbitrary-length videos, but also arbitrary aspect ratios and scales.
It reminds me of the spatial pyramid pooling in deep convolutional networks. In CNN, the dimensions of the training data are the same, so that after convolution, we can train the classifiers effectively. To improve the limit of the same dimension, spatial pyramid pooling is introduced.
Overall Architecture

The following are the components of the DANN (as shown in Figure 3)
- 6 Alternative layers with 64, 128, 256, 256, 512 and 512 kernel response maps
- 5 ReLU and volumetric pooling layers
- 1 volumetric pyramid pooling layer
- 3 fully connected layers of size 2048 each
- A softmax layer
Implementation details
The authors have used the Torch toolbox platform for implementations of volumetric convolutions, recurrent layers, and optimizations. They have used a technique called as random clipping for data augmentation, in which they select a point randomly from the input video of fixed size 80x80xt after determining the temporal size t. This technique is preferred to the common alternative of pre-processing data using a sliding window approach to have pre-segmented clips. The authors cite how using this technique limits the amount of data when the windows are not overlapped with one another. For training the network the authors have used SGD applied to mini-batches of size 30 with a negative log likelihood criterion. Training is done by minimizing the cross-entropy loss function using backpropagation through time algorithm (BPTT). During testing, they applied a video clip divided into 80x80xt clips with a stride of 4 frames followed by testing with 10 crops. The final score is the average of all clip-level scores and the crop scores. Data augmentation techniques such as the multi-scale cropping method have been evaluated due to the recent success in the state-of-the-art performance displayed by Very Deep Two-stream ConvNets. Going by intuition, the corner cropping strategy could provide better results ( based on trade-off degree) since the receptive fields can focus harder on the central regions of the video frames [7].
Evaluations
Datasets:
- The datasets used in the evaluation are UCF101 and HMDB51
- UCF101 – 13K videos annotated into 101 classes
- HMDB51 – 6.8K videos with 51 actions.
- Three training and test splits are provided
- Performance measured by mean classification accuracy across the splits.
- UCF101 split – 9.5K videos; HMDB51 – 3.7K training videos.
Quantitative Results
The authors used three types of optical flows, viz., sparse, RGB and TVL1 and found that TVL1 is suitable as action recognition is more easy to learn from motion information compared to raw pixel values. The influence of data augmentation is also studied. The baseline being sliding window with 75% overlap, the authors observed that the random clipping and multi-scale clipping outperformed the baseline on the UCF101 split 1 dataset. The authors were able to prove that the adaptive temporal length was able to give a boost of 4.2% when compared with architectures that had fixed-size temporal length. Experiments were also conducted to see if the learnings done in one dataset could improve the accuracy of another dataset. Fine tuning HMDB51 from UCF101 boosted the performance from 56.4% to 62.5%. The authors also observed that increasing the AL layers improves the performance as larger contexts are being embedded into the DANN. The DANN achieved an overall accuracy of 65.9% and 91.6% on HMDB51 and UCF101 respectively.
Qualitative Analysis
The authors have discussed the quality of the prediction in the video clips taking examples of two different scenes involving bowling and haircut. In the bowling scene, the adaptive temporal choice used by DANN could aggregate more reasonable semantic structures and hence it leveraged reasonable video clips as input. On the other hand, the performance on the haircut video clip was not up to the mark as the rich contexts provided by the DANN was not helpful in a setting with simple actions performed in a simple background.
Conclusions and Critique
- Deep alternative neural network is introduced for action recognition.
- The key new component is an "alternative layer" which is composed of a convolutional layer followed by a recurrent layer. As the paper targets action recognition in video, the convolutional layer acts on a 3D spatio-temporal volume.
- DANN consists of volumetric convolutional layer and a recurrent layer.
- A preprocessing stage based on optical flow is used to select video fragments to feed to the neural network.
- The authors have experimented with different datasets like HMDB51 and UCF101 with different scenarios and compared the * * performance of DANN with other approaches.
- The spatial size is still chosen in an ad hoc manner and this can be an area of improvement.
- There are prospects for studying action tube which is a more compact input.
- The paper uses volumetric convolutional layer, but it doesn't say how it is better than recurrent neural networks in exploring temporal information.
- There is no experimental evidence to compare the proposed method with long-term recurrent convolutional network. Also, there is no analysis of time complexity of the approach used.
Github code: https://github.com/wangjinzhuo/DANN
In the formal review of the paper [1], some interesting criticisms of the paper are surfaced. For starters, one reviewer notes that a similar architecture was proposed in [2], limiting the novelty of the approach somewhat. The reviewers question the validity of the approach in even slightly more complicated settings (i.e. any non-static camera, which brings in the issue of optical flow). Other criticisms come from a lack of clear motivation for choices that the authors have made, for instance, the use of Local Response Normalization has fallen slightly out-of-favour, or the benefit of using a sliding window approach during testing (and random clips during training).
Quantitatively, the benefits of the author's approach are not readily apparent. In comparisons with state-of-the-art, the proposed model performs worse on HMDB, and while they claim the highest performance on UCF, the increase is merely .1 over previous best efforts.
References
[1] Andrej Karpathy, George Toderici, Sachin Shetty, Tommy Leung, Rahul Sukthankar, and Li FeiFei. Large-scale video classification with convolutional neural networks. In CVPR, pages 1725–1732, 2014
[2] Karen Simonyan and Andrew Zisserman. Two-stream convolutional networks for action recognition in videos. In NIPS, pages 568–576, 2014.
[3]Limin Wang, Yu Qiao, and Xiaoou Tang. Action recognition with trajectory-pooled deepconvolutional descriptors. In CVPR, pages 4305–4314, 2015.
[4] Shuiwang Ji, Wei Xu, Ming Yang, and Kai Yu. 3d convolutional neural networks for human action recognition. TPAMI, 35(1):221–231, 2013.
[5] Du Tran, Lubomir Bourdev, Rob Fergus, Lorenzo Torresani, and Manohar Paluri. Learning spatiotemporal features with 3d convolutional networks. In ICCV, pages 4489–4497, 2015.
[6]Gül Varol, Ivan Laptev, and Cordelia Schmid. Long-term temporal convolutions for action recognition. arXiv preprint arXiv:1604.04494, 2016.
[7]Limin Wang, Yuanjun Xiong, Zhe Wang, Yu Qiao. Towards Good Practices for Very Deep Two-Stream ConvNets. arXiv preprint arXiv:1507.02159 , 2015.
[8] IEEE International Symposium on Multimedia 2013
[9] Gül Varol, Ivan Laptev, and Cordelia Schmid. Long-term temporal convolutions for action recognition. arXiv preprint arXiv:1604.04494, 2016
[10] https://en.wikipedia.org/wiki/Optical_flow
[11] Delving Deeper into Convolutional Networks for Learning Video Representations Nicolas Ballas, Li Yao, Chris Pal, Aaron Courville, ICLR 2016
[12] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Spatial pyramid pooling in deep convolutional networks for visual recognition. TPAMI, 37(9):1904–1916, 2015.
[13] Christopher Zach, Thomas Pock, and Horst Bischof. A duality based approach for realtime tv-l 1 optical flow. In Pattern Recognition, pages 214–223. 2007.
A list of expert reviews: http://media.nips.cc/nipsbooks/nipspapers/paper_files/nips29/reviews/480.html