DeepVO Towards end to end visual odometry with deep RNN
Introduction
Visual Odometry (VO) is a computer vision technique for estimating an object’s position and orientation from camera images. It is an important technique commonly used for “pose estimation and robot localization”, with notable applications on the Mars Exploration Rovers and Autonomous Vehicles [x1] [x2]. While the research field of VO is broad, this paper focuses on the topic of monocular visual odometry. Particularly, the authors examine prominent VO methods and argue mainstream geometry based monocular VO methods should be amended with deep learning approaches. Subsequently, the paper proposes a novel deep-learning based end-to-end VO algorithm, and then empirically demonstrates its viability.
Related Work
Visual odometry algorithms can be grouped into two main categories. The first is known as the conventional methods, and they are based on established principles of geometry. Specifically, an object’s position and orientation are obtained by identifying reference points and calculating how those points change over the image sequence. Moreover, algorithms in this category can be divided into two sub-categories, which differ by how they select reference points. Namely, sparse feature based methods establish reference points using image salient features, such as corners and edges [8]. Whereas, direct methods make use of the whole image and consider every pixel as a reference point [11]. Furthermore, semi-direct methods that combine both approaches are recently gaining popularity [16].
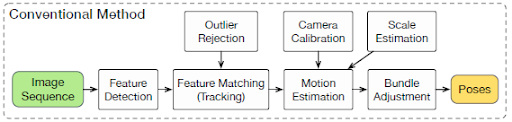
Today, most of state-of-the-art VO algorithms belong to the geometry family. However, they have significant limitations. For example, direct methods assume “photometric consistency” [11]. Whereas, sparse feature methods are prone to “drifting” because of outliers and noises. As the result, the paper argues geometry-based methods are difficult to engineer and calibrate, thus limiting its practicality. Figure 1 illustrates the general architecture of geometry-based algorithms, and it outlines necessary drift correction techniques such as Camera Calibration, Feature Detection, Feature Matching (tracking), Outlier Rejection, Motion Estimation, Scale Estimation, and Local optimization (bundle adjustment).
Figure 1. Architectures of the conventional geometry-based monocular VO method.
The second category of VO algorithms is based on learning. Namely, they try to learn an object’s “motion model’ from labeled optical flows. Initially, these models are trained using classic Machine Learning techniques such as KNN [15], Gaussian Process [16], and Support Vector Machines[17]. However, these models were inefficient to handle “highly non-linear and high dimensional” inputs, which cause them to perform poorly in comparison with geometry-based methods. For this reason, Deep Learning-based approaches are dominating research in this field and producing many promising results. For example, CNN based models can now recognize places based on appearance [18] and detect direction and velocity from stereo inputs [20]. Moreover, a deep learning model even achieves “robust VO with blurred and under-exposed images [21]”. While these successes are encouraging, the authors observe that a CNN based architecture is “incapable of modeling sequential information”. Instead, they propose to use RNN to tackle this problem.
End-to-End Visual odometry through RCNN
Architecture Overview
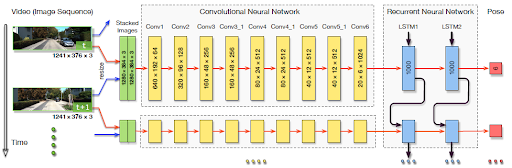
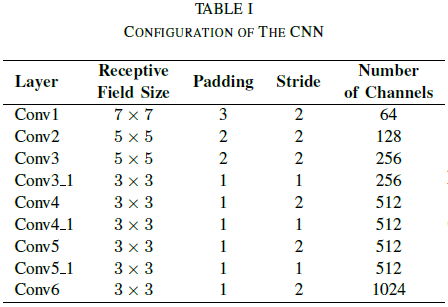
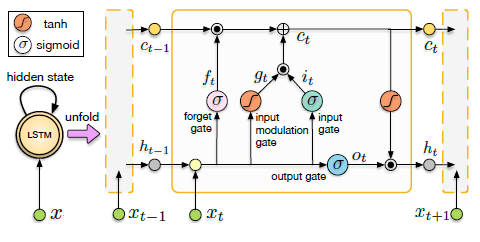
An end-to-end monocular VO model is proposed by utilizing deep Recurrence Convolutional Neural Network (RCNN). Figure 2 depicts the end-to-end model, which is comprised of three main stages. First, the model takes a monocular video as input and it pre-processes the image sequence by “subtracting the mean RGB values” from each frame. Then, consecutive image frames are stacked to form tensors, which become the inputs for the CNN stage. The purpose of the CNN stages is to extract salient features from the input image. The structure of the CNN is inspired by FlowNet [24] and designed to model optimal flows. Details of the CNN structure is shown in Table 1. Using CNN features as input, the RNN stage tries to estimate the temporal and sequential relations among input features. The RNN network is composed of two Long Short-Term Memory networks (LSTM), which allows the network to make predictions based on long-term and short-term dependencies. Figure 3 illustrated the structure. In this way, the RCNN architecture allows for end-to-end pose estimation for each time step.
Figure 2. Architectures of the proposed RCNN based monocular VO system.
Table 1. CNN structure
Figure 3. Folded and unfolded LSTMs and its internal structure.
Training and Optimisation
The proposed RCNN model can be represented as a conditional probability of poses given an image sequence: p(Yt|Xt) = p(y1,...,yt|x1,...,xt). Given this probability function is expressed as a deep RCNN, the problem can be interpreted as finding the hyperparameters or network weights that minimize the loss function between actual and predicted poses, in which the loss function, is chosen to be Mean Square Error (MSE) of all positions and orientation.