DeepVO Towards end to end visual odometry with deep RNN: Difference between revisions
| (24 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
Visual Odometry (VO) is a computer vision technique for estimating an object’s position and orientation from camera images. It is an important technique commonly used for “pose estimation and robot | Visual Odometry (VO) is a computer vision technique for estimating an object’s position and orientation from camera images. It is an important technique commonly used for “pose estimation and robot localization” with notable applications in Mars Exploration Rovers and Autonomous Vehicles [x1] [x2]. While the research field of VO is broad, this paper focuses on the topic of monocular visual odometry. Particularly, the authors examine prominent VO methods and argue that mainstream geometry based monocular VO methods should be amended with deep learning approaches. Deep Learning (DL) has recently achieved promising results in computer vision tasks but does not include the VO field, thus the paper proposes a novel deep-learning based end-to-end VO algorithm and then empirically demonstrates its viability. | ||
== Related Work == | == Related Work == | ||
| Line 6: | Line 6: | ||
Visual odometry algorithms can be grouped into two main categories. The first is known as the conventional methods, and they are based on established principles of geometry. Specifically, an object’s position and orientation (pose) are obtained by identifying reference points and calculating how those points change over the image sequence. Algorithms in this category can be further divided into two: sparse feature based methods and direct methods, which differ in the method employed to select reference points. Sparse feature based methods establish reference points using image salient features such as corners and edges [8]. Direct methods, on the other hand, make use of the whole image and consider every pixel as a reference point [11]. Recently, semi-direct methods that combine the benefits of both approaches are gaining popularity [16]. | Visual odometry algorithms can be grouped into two main categories. The first is known as the conventional methods, and they are based on established principles of geometry. Specifically, an object’s position and orientation (pose) are obtained by identifying reference points and calculating how those points change over the image sequence. Algorithms in this category can be further divided into two: sparse feature based methods and direct methods, which differ in the method employed to select reference points. Sparse feature based methods establish reference points using image salient features such as corners and edges [8]. Direct methods, on the other hand, make use of the whole image and consider every pixel as a reference point [11]. Recently, semi-direct methods that combine the benefits of both approaches are gaining popularity [16]. | ||
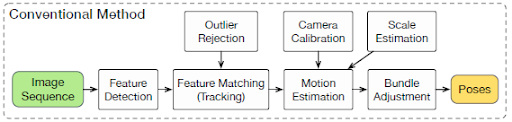
Today, most of the state-of-the-art VO algorithms belong to the geometry family. However, they suffer significant limitations. For example, direct methods assume “photometric consistency” [11]. Sparse feature based methods are also prone to “drifting” because of outliers and noises. As a result, the paper argues that geometry-based methods are difficult to engineer and calibrate, limiting | Today, most of the state-of-the-art VO algorithms belong to the geometry family. However, they suffer significant limitations. For example, direct methods assume “photometric consistency” [11]. Sparse feature based methods are also prone to “drifting” because of outliers and noises. As a result, the paper argues that geometry-based methods are difficult to engineer and calibrate, limiting their practicality. Figure 1 illustrates the general architecture of geometry-based algorithms. It outlines necessary drift correction techniques such as Camera Calibration, Feature Detection, Feature Matching (tracking), Outlier Rejection, Motion Estimation, Scale Estimation, and Local optimization (bundle adjustment). | ||
[[File:DeepVO_Figure_1.png | center]] | [[File:DeepVO_Figure_1.png | center]] | ||
| Line 12: | Line 12: | ||
<div align="center">Figure 1. Architectures of the conventional geometry-based monocular VO method.</div> | <div align="center">Figure 1. Architectures of the conventional geometry-based monocular VO method.</div> | ||
The second category of VO algorithms is based on learning. Namely, they try to learn an object’s motion model from labeled optical flows. Initially, these models are trained using classic Machine Learning techniques such as k-nearest neighbors (KNNs) [15], Gaussian Processes [16], and Support Vector Machines [17]. However, these models were inefficient to handle highly non-linear and high-dimensional inputs, leading to poor performance in comparison with geometry-based methods. | The second category of VO algorithms is based on learning. Namely, they try to learn an object’s motion model from labeled optical flows. Initially, these models are trained using classic Machine Learning techniques such as k-nearest neighbors (KNNs) [15], Gaussian Processes [16], and Support Vector Machines [17]. However, these models were inefficient to handle highly non-linear and high-dimensional inputs, leading to poor performance in comparison with geometry-based methods. More recently, deep learning based approaches are dominating research and are producing many promising results. For example, Convolutional Neural Network (CNN) based models can now recognize places based on appearance [18] and detect direction and velocity from stereo inputs [20]. Moreover, a deep learning model even achieved robust VO with blurred and under-exposed images [21]. While these successes are encouraging, the authors observe that a CNN based architecture is “incapable of modeling sequential information.” Instead, they proposed to use Recurrent Neural networks (RNN) to tackle this problem. | ||
== End-to-End Visual odometry through RCNN == | == End-to-End Visual odometry through RCNN == | ||
=== Architecture Overview === | === Architecture Overview === | ||
An end-to-end monocular VO model is proposed by utilizing deep Recurrence Convolutional Neural Network (RCNN). Figure 2 depicts the end-to-end model, which is comprised of three main stages. First, the model takes a monocular video as input and pre-processes the image sequences by “subtracting the mean RGB values of all frames” from each frame. Then, consecutive image sequences are stacked to form tensors, which become the inputs for the CNN stage. The purpose of the CNN stages is to extract salient features from the image tensors. The structure of the CNN is inspired by FlowNet [24], which is a model designed to extract optical flows. Details of the CNN structure is shown in Table 1. Using CNN optical flow features as input, the RNN stage tries to estimate the temporal and sequential relations among the features. The RNN stage does this by utilizing two Long Short-Term Memory networks (LSTM), which estimate object poses for each time step using both long-term and short-term dependencies. Figure 3 illustrates the RNN architecture. | An end-to-end monocular VO model is proposed by utilizing deep Recurrence Convolutional Neural Network (RCNN). Figure 2 depicts the end-to-end model, which is comprised of three main stages. First, the model takes a monocular video as input and pre-processes the image sequences by “subtracting the mean RGB values of all frames” from each frame. Then, consecutive image sequences are stacked to form tensors, which become the inputs for the CNN stage. The purpose of the CNN stages is to extract salient features from the image tensors. The structure of the CNN is inspired by FlowNet [24], which is a model designed to extract optical flows. Details of the CNN structure is shown in Table 1. In this architecture, the size of the receptive fields in the network are gradually reduced from 7x7 to 5x5 and then to 3x3 to capture small interesting features. Zero-paddings are introduced either adapt to the configurations of receptive fields or preserve the spatial dimension of the tensor after convolution. The CNN takes raw RGB images as input. The output is a compressed representation of the features of optical flow. Using CNN optical flow features as input, the RNN stage tries to estimate the temporal and sequential relations among the features. The RNN stage does this by utilizing two Long Short-Term Memory networks (LSTM), which estimate object poses for each time step using both long-term and short-term dependencies. Figure 3 illustrates the RNN architecture. | ||
Without the LSTM framework, RNNs often experience vanishing gradients or gradient exploding. If the gradient is small and the network is deep, when it is propagated to the shallower layers during the backward pass, it often just becomes too small to have an effect on the weights. This forces standard RNN architectures to be relatively shallow for temporal prediction over time. In other words, the weight update for recent events will have a much larger effect on the network weights than events happened long-time ago. Visual odometry is a very complex problem, and thus we attempt to learn highly complex functions within the network. Hence, to circumvent the vanishing gradient issue, we use LSTM nodes. Conversely, LSTM can handle long-term dependencies and has deep temporal structure, but needs depth on network layers to learn complex high-level representation. LSTM define three additional gates: forget gate, input gate and update gate to help better capture the long-term dependencies. Deep RNNs have been shown to perform well on complex dynamic representations (e.g. speech recognition), and thus we leverage this architecture and layer multiple LSTM layers to mitigate vanishing gradient without losing the network's ability to represent complex dynamics. | |||
Additionally, LSTM architectures can provide a mechanism to extract not only patterns from past timeframes but also from future timeframes, which means that if there is not a requirement for real-time odometry, the overall accuracy can be improved by using bi-directional LSTM cells to refine the estimation of current location and orientation in the coordinate system. Although it requires significantly more computational resources, by implementing bi-directional LSTM cells a monocular vision system can alleviate some of the limitations caused by the available single point of view. | |||
[[File:DeepVO_Figure_2.png | center]] | [[File:DeepVO_Figure_2.png | center]] | ||
| Line 29: | Line 33: | ||
=== Training and Optimization === | === Training and Optimization === | ||
The proposed RCNN model can be represented as a conditional probability of poses given an image sequence: | The proposed RCNN model can be represented as a conditional probability of poses <math> Y_{t} = (y_{1},...y_{t}) </math> given an image sequence <math> X_{t} = (x_{1},...x_{t}) </math>: | ||
\begin{align} | |||
p(Y_{t}|X_{t}) = p(y_{1},...,y_{t}|x_{1},...,x_{t}) | p(Y_{t}|X_{t}) = p(y_{1},...,y_{t}|x_{1},...,x_{t}) | ||
\end{align} | |||
To find optimal parameters, the Deep Neural Networks (DNN) maximizes: | |||
To find | |||
\begin{align} | |||
\ | \theta^{*}=argmax(Y{t}|X{t};\theta) | ||
\end{align} | |||
To learn the | To learn the parameters <math>\theta</math> of the DNNs, the Euclidean distance between the ground truth pose <math>(p_k,\phi_k)</math> at time <math>k</math> and its estimated one <math>(\hat{p}_k,\hat{\phi}_k)</math> is minimized. The loss function is composed of Mean Square Error (MSE) of all positions <math>p</math> and orientations <math>\varphi</math> minimizes: | ||
\begin{align} | |||
\ | \theta^{*}=argmin\frac{1}{N}\sum_{N}^{i=1}\sum_{t}^{k=1}||\hat{p}_{k}-p_{k}||_{2}^{2}+\kappa||\hat{\varphi}_{k}-\varphi_{k}||_{2}^{2} | ||
\end{align} | |||
where || *|| is <math>L_{2} | where <math>|| *||</math> is <math>L_{2}</math> norm, <math>\kappa</math> (100 in the experiments) is a scale factor to balance the weights of positions and orientations, <math>N</math> is the number of samples, and the orientation <math>φ</math> is represented by Euler angles. | ||
== Experiments and Results == | == Experiments and Results == | ||
| Line 56: | Line 59: | ||
[[File:DeepVO_Table_2.png | center]] | [[File:DeepVO_Table_2.png |500px| center]] | ||
[[File:DeepVO_Figure_6.png | center]] | [[File:DeepVO_Figure_6.png |500px| center]] | ||
| Line 65: | Line 68: | ||
[[File:DeepVO_Figure_8.png | center]] | [[File:DeepVO_Figure_8.png |600px| center]] | ||
== Conclusions == | |||
The paper presents a new RCNN VO model that combines the CNNs with the RNNs under the power of Deep RCNNs. It can achieve representation learning while sequential modeling of the monocular VO. Although it is considered a viable approach, it is not expected to be a replacement to the classic geometry-based approach. However, from the experiment result, it can be a viable complement by combining geometry and DNN learning representations, knowledge and models to further improve VO's accuracy and robustness. The main contribution of the paper is threefold: | |||
# The authors demonstrate that the monocular VO problem can be addressed in an end-to-end fashion based on DL, i.e., directly estimating poses from raw RGB images. Neither prior knowledge nor parameter is needed to recover the absolute scale. | |||
#The authors propose a RCNN architecture enabling the DL based VO algorithm to be generalised to totally new environments by using the geometric feature representation learned by the CNN. | |||
of an image sequence, which are of importance to the VO but cannot be explicitly or easily | # Sequential dependence and complex motion dynamics of an image sequence, which are of importance to the VO but cannot be explicitly or easily modeled by a human, are implicitly encapsulated and automatically learnt by the RCNN. | ||
== Critiques == | == Critiques == | ||
This paper cannot be considered as a critical advance to the state of the art as the authors just suggest a method combining CNN and RNNs for the visual odometry problem. The authors also state that deep learning in terms of simple feed-forward Neural networks and CNNs has already been used in this problem. Only an RNN approach seems to have been not tried on this problem. The authors propose a combined RCNN and geometric-based approach towards the end of the paper. But | This paper cannot be considered as a critical advance to the state of the art as the authors just suggest a method combining CNN and RNNs for the visual odometry problem. The authors also state that deep learning in terms of simple feed-forward Neural networks and CNNs has already been used in this problem. Only an RNN approach seems to have been not tried on this problem. The authors propose a combined RCNN and geometric-based approach towards the end of the paper. But it is not intuitive how these two potentially very diverse methods could be combined. The authors also do not explain any proposed methods for the combination. The authors don't build a compelling case against the state of the art methods or convincingly prove the superiority of the RCNN or a combined method. For example, the RCNN and other state of the art geometry-based methods have a deficiency of getting lower accuracies when shown a large open area in the images as mentioned by the authors. The authors put forth some techniques to solve this problem for the geometry approaches but they state that they do not have a similar method for the deep learning based approaches. Thus, in such scenarios, the methods proposed by the authors don't seem to work at all. | ||
The paper advances the field of deep-learning based VO by creating a pioneering end-to-end model that is capable of extracting features and learning sequential dynamics from monocular videos. While the new model clearly outperforms the LIBVISO2_M algorithm, it fails to demonstrate any advantage over the LIBVISO2_S algorithm. Hence, it makes one question whether the complexity of deep-learning based monocular VO methods is justified | The paper advances the field of deep-learning based VO by creating a pioneering end-to-end model that is capable of extracting features and learning sequential dynamics from monocular videos. While the new model clearly outperforms the LIBVISO2_M algorithm, it fails to demonstrate any advantage over the LIBVISO2_S algorithm. Hence, it makes one question whether the complexity of deep-learning based monocular VO methods is justified and whether robots or autonomous vehicles designers should opt for stereo visions as much as possible. Nonetheless, this end-to-end model is beneficial for situations where monocular VO is the only viable option. Furthermore, the paper could have benefited by including a qualitative comparison of the algorithm’s computation requirements, such as hardware specification, engineering time, and training time. Though the justification for input sequence pre-processing is not explained completely, it can be attributed to the fact that they are using standard pre-processing techniques like mean Subtraction and normalization, which helps in easier optimization of cost functions. Perhaps, future-works could involve adapting the model for real-time visual odometry. | ||
== Other Sources == | |||
# Code (not original authors) can be found at [https://github.com/sladebot/deepvo] and [https://github.com/themightyoarfish/deepVO]. | |||
# Presentation slides can be found here [https://www.slideshare.net/JackyLiu40/deepvo-towards-visual-odometry-with-deep-learning]. | |||
== References == | == References == | ||
| Line 104: | Line 113: | ||
[24] A. Dosovitskiy, P. Fischery, E. Ilg, C. Hazirbas, V. Golkov, P. van der Smagt, D. Cremers, T. Brox et al., “Flownet: Learning optical flow with convolutional networks,” in Proceedings of IEEE International Conference on Computer Vision (ICCV). IEEE, 2015, pp. 2758–2766. | [24] A. Dosovitskiy, P. Fischery, E. Ilg, C. Hazirbas, V. Golkov, P. van der Smagt, D. Cremers, T. Brox et al., “Flownet: Learning optical flow with convolutional networks,” in Proceedings of IEEE International Conference on Computer Vision (ICCV). IEEE, 2015, pp. 2758–2766. | ||
[25]http://cs231n.github.io/neural-networks-2/ | |||
Latest revision as of 18:30, 16 December 2018
Introduction
Visual Odometry (VO) is a computer vision technique for estimating an object’s position and orientation from camera images. It is an important technique commonly used for “pose estimation and robot localization” with notable applications in Mars Exploration Rovers and Autonomous Vehicles [x1] [x2]. While the research field of VO is broad, this paper focuses on the topic of monocular visual odometry. Particularly, the authors examine prominent VO methods and argue that mainstream geometry based monocular VO methods should be amended with deep learning approaches. Deep Learning (DL) has recently achieved promising results in computer vision tasks but does not include the VO field, thus the paper proposes a novel deep-learning based end-to-end VO algorithm and then empirically demonstrates its viability.
Related Work
Visual odometry algorithms can be grouped into two main categories. The first is known as the conventional methods, and they are based on established principles of geometry. Specifically, an object’s position and orientation (pose) are obtained by identifying reference points and calculating how those points change over the image sequence. Algorithms in this category can be further divided into two: sparse feature based methods and direct methods, which differ in the method employed to select reference points. Sparse feature based methods establish reference points using image salient features such as corners and edges [8]. Direct methods, on the other hand, make use of the whole image and consider every pixel as a reference point [11]. Recently, semi-direct methods that combine the benefits of both approaches are gaining popularity [16].
Today, most of the state-of-the-art VO algorithms belong to the geometry family. However, they suffer significant limitations. For example, direct methods assume “photometric consistency” [11]. Sparse feature based methods are also prone to “drifting” because of outliers and noises. As a result, the paper argues that geometry-based methods are difficult to engineer and calibrate, limiting their practicality. Figure 1 illustrates the general architecture of geometry-based algorithms. It outlines necessary drift correction techniques such as Camera Calibration, Feature Detection, Feature Matching (tracking), Outlier Rejection, Motion Estimation, Scale Estimation, and Local optimization (bundle adjustment).
The second category of VO algorithms is based on learning. Namely, they try to learn an object’s motion model from labeled optical flows. Initially, these models are trained using classic Machine Learning techniques such as k-nearest neighbors (KNNs) [15], Gaussian Processes [16], and Support Vector Machines [17]. However, these models were inefficient to handle highly non-linear and high-dimensional inputs, leading to poor performance in comparison with geometry-based methods. More recently, deep learning based approaches are dominating research and are producing many promising results. For example, Convolutional Neural Network (CNN) based models can now recognize places based on appearance [18] and detect direction and velocity from stereo inputs [20]. Moreover, a deep learning model even achieved robust VO with blurred and under-exposed images [21]. While these successes are encouraging, the authors observe that a CNN based architecture is “incapable of modeling sequential information.” Instead, they proposed to use Recurrent Neural networks (RNN) to tackle this problem.
End-to-End Visual odometry through RCNN
Architecture Overview
An end-to-end monocular VO model is proposed by utilizing deep Recurrence Convolutional Neural Network (RCNN). Figure 2 depicts the end-to-end model, which is comprised of three main stages. First, the model takes a monocular video as input and pre-processes the image sequences by “subtracting the mean RGB values of all frames” from each frame. Then, consecutive image sequences are stacked to form tensors, which become the inputs for the CNN stage. The purpose of the CNN stages is to extract salient features from the image tensors. The structure of the CNN is inspired by FlowNet [24], which is a model designed to extract optical flows. Details of the CNN structure is shown in Table 1. In this architecture, the size of the receptive fields in the network are gradually reduced from 7x7 to 5x5 and then to 3x3 to capture small interesting features. Zero-paddings are introduced either adapt to the configurations of receptive fields or preserve the spatial dimension of the tensor after convolution. The CNN takes raw RGB images as input. The output is a compressed representation of the features of optical flow. Using CNN optical flow features as input, the RNN stage tries to estimate the temporal and sequential relations among the features. The RNN stage does this by utilizing two Long Short-Term Memory networks (LSTM), which estimate object poses for each time step using both long-term and short-term dependencies. Figure 3 illustrates the RNN architecture.
Without the LSTM framework, RNNs often experience vanishing gradients or gradient exploding. If the gradient is small and the network is deep, when it is propagated to the shallower layers during the backward pass, it often just becomes too small to have an effect on the weights. This forces standard RNN architectures to be relatively shallow for temporal prediction over time. In other words, the weight update for recent events will have a much larger effect on the network weights than events happened long-time ago. Visual odometry is a very complex problem, and thus we attempt to learn highly complex functions within the network. Hence, to circumvent the vanishing gradient issue, we use LSTM nodes. Conversely, LSTM can handle long-term dependencies and has deep temporal structure, but needs depth on network layers to learn complex high-level representation. LSTM define three additional gates: forget gate, input gate and update gate to help better capture the long-term dependencies. Deep RNNs have been shown to perform well on complex dynamic representations (e.g. speech recognition), and thus we leverage this architecture and layer multiple LSTM layers to mitigate vanishing gradient without losing the network's ability to represent complex dynamics.
Additionally, LSTM architectures can provide a mechanism to extract not only patterns from past timeframes but also from future timeframes, which means that if there is not a requirement for real-time odometry, the overall accuracy can be improved by using bi-directional LSTM cells to refine the estimation of current location and orientation in the coordinate system. Although it requires significantly more computational resources, by implementing bi-directional LSTM cells a monocular vision system can alleviate some of the limitations caused by the available single point of view.
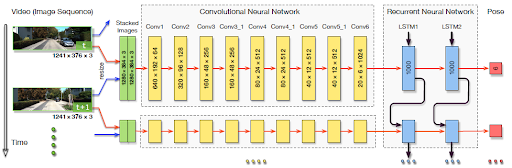
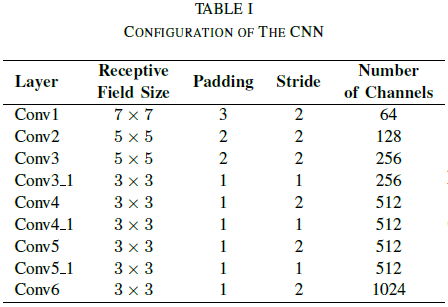
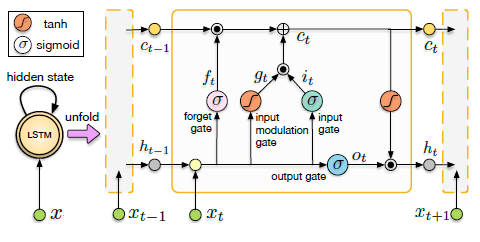
Training and Optimization
The proposed RCNN model can be represented as a conditional probability of poses [math]\displaystyle{ Y_{t} = (y_{1},...y_{t}) }[/math] given an image sequence [math]\displaystyle{ X_{t} = (x_{1},...x_{t}) }[/math]:
\begin{align} p(Y_{t}|X_{t}) = p(y_{1},...,y_{t}|x_{1},...,x_{t}) \end{align}
To find optimal parameters, the Deep Neural Networks (DNN) maximizes:
\begin{align} \theta^{*}=argmax(Y{t}|X{t};\theta) \end{align}
To learn the parameters [math]\displaystyle{ \theta }[/math] of the DNNs, the Euclidean distance between the ground truth pose [math]\displaystyle{ (p_k,\phi_k) }[/math] at time [math]\displaystyle{ k }[/math] and its estimated one [math]\displaystyle{ (\hat{p}_k,\hat{\phi}_k) }[/math] is minimized. The loss function is composed of Mean Square Error (MSE) of all positions [math]\displaystyle{ p }[/math] and orientations [math]\displaystyle{ \varphi }[/math] minimizes:
\begin{align} \theta^{*}=argmin\frac{1}{N}\sum_{N}^{i=1}\sum_{t}^{k=1}||\hat{p}_{k}-p_{k}||_{2}^{2}+\kappa||\hat{\varphi}_{k}-\varphi_{k}||_{2}^{2} \end{align}
where [math]\displaystyle{ || *|| }[/math] is [math]\displaystyle{ L_{2} }[/math] norm, [math]\displaystyle{ \kappa }[/math] (100 in the experiments) is a scale factor to balance the weights of positions and orientations, [math]\displaystyle{ N }[/math] is the number of samples, and the orientation [math]\displaystyle{ φ }[/math] is represented by Euler angles.
Experiments and Results
The paper evaluates the proposed RCNN VO model by comparing it empirically with the open-source VO library of LIBVISO2 [7], which is a well-known geometry based model. The comparison is done using the KITTI VO/SLAM benchmark [3], which contains 22 image sequences, 11 of which are labeled with ground truths. Two separate experiments are performed.
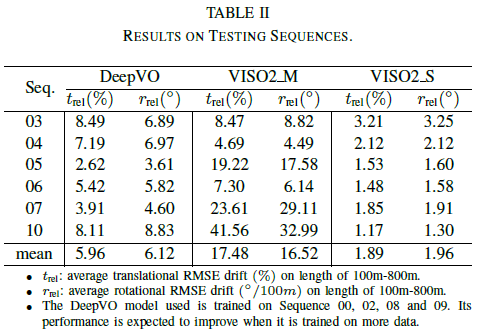
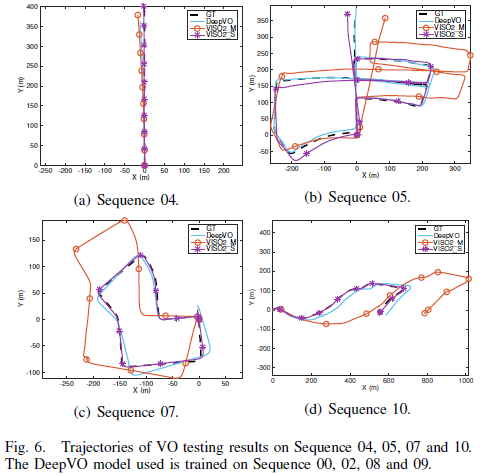
1. Quantitatively Analysis is performed using only labeled image sequence. Namely, 4 of 11 image sequences were used for training and the others reserved for testing. Table 2 and Figure 6 outlines the result, showing that the proposed RCNN model performs consistently better than the monocular VISO2_M model. However, it performs worse than the stereo VISO2_S model.
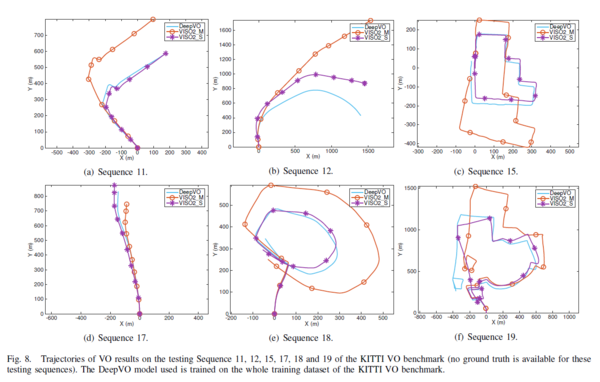
2. The generalizability of the proposed RCNN model is evaluated using the unlabeled image sequences. Figure 8 outlines the test result, showing that the proposed model is able to generalize better than the monocular VISO2_M model and performs roughly the same as the stereo VISO2_S model.
Conclusions
The paper presents a new RCNN VO model that combines the CNNs with the RNNs under the power of Deep RCNNs. It can achieve representation learning while sequential modeling of the monocular VO. Although it is considered a viable approach, it is not expected to be a replacement to the classic geometry-based approach. However, from the experiment result, it can be a viable complement by combining geometry and DNN learning representations, knowledge and models to further improve VO's accuracy and robustness. The main contribution of the paper is threefold:
- The authors demonstrate that the monocular VO problem can be addressed in an end-to-end fashion based on DL, i.e., directly estimating poses from raw RGB images. Neither prior knowledge nor parameter is needed to recover the absolute scale.
- The authors propose a RCNN architecture enabling the DL based VO algorithm to be generalised to totally new environments by using the geometric feature representation learned by the CNN.
- Sequential dependence and complex motion dynamics of an image sequence, which are of importance to the VO but cannot be explicitly or easily modeled by a human, are implicitly encapsulated and automatically learnt by the RCNN.
Critiques
This paper cannot be considered as a critical advance to the state of the art as the authors just suggest a method combining CNN and RNNs for the visual odometry problem. The authors also state that deep learning in terms of simple feed-forward Neural networks and CNNs has already been used in this problem. Only an RNN approach seems to have been not tried on this problem. The authors propose a combined RCNN and geometric-based approach towards the end of the paper. But it is not intuitive how these two potentially very diverse methods could be combined. The authors also do not explain any proposed methods for the combination. The authors don't build a compelling case against the state of the art methods or convincingly prove the superiority of the RCNN or a combined method. For example, the RCNN and other state of the art geometry-based methods have a deficiency of getting lower accuracies when shown a large open area in the images as mentioned by the authors. The authors put forth some techniques to solve this problem for the geometry approaches but they state that they do not have a similar method for the deep learning based approaches. Thus, in such scenarios, the methods proposed by the authors don't seem to work at all.
The paper advances the field of deep-learning based VO by creating a pioneering end-to-end model that is capable of extracting features and learning sequential dynamics from monocular videos. While the new model clearly outperforms the LIBVISO2_M algorithm, it fails to demonstrate any advantage over the LIBVISO2_S algorithm. Hence, it makes one question whether the complexity of deep-learning based monocular VO methods is justified and whether robots or autonomous vehicles designers should opt for stereo visions as much as possible. Nonetheless, this end-to-end model is beneficial for situations where monocular VO is the only viable option. Furthermore, the paper could have benefited by including a qualitative comparison of the algorithm’s computation requirements, such as hardware specification, engineering time, and training time. Though the justification for input sequence pre-processing is not explained completely, it can be attributed to the fact that they are using standard pre-processing techniques like mean Subtraction and normalization, which helps in easier optimization of cost functions. Perhaps, future-works could involve adapting the model for real-time visual odometry.
Other Sources
References
[1] S. Wang, R. Clark, H. Wen and N. Trigoni, "DeepVO: Towards end-to-end visual odometry with deep Recurrent Convolutional Neural Networks," 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 2017, pp. 2043-2050.
[2] M. Maimone, Y. Cheng, and L. Matthies, "Two years of Visual Odometry on the Mars Exploration Rovers," Journal of Field Robotics. 24 (3): 169–186, 2007.
[3] A. Geiger, P. Lenz, and R. Urtasun, “Are we ready for autonomous driving? the KITTI vision benchmark suite,” in Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2012.
[7] A. Geiger, J. Ziegler, and C. Stiller, “Stereoscan: Dense 3D reconstruction in real-time,” in Intelligent Vehicles Symposium (IV), 2011.
[8] A. J. Davison, I. D. Reid, N. D. Molton, and O. Stasse, “MonoSLAM: Real-time single camera SLAM,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 29, no. 6, pp. 1052–1067, 2007.
[11] R. A. Newcombe, S. J. Lovegrove, and A. J. Davison, “DTAM: Dense tracking and mapping in real-time,” in Proceedings of IEEE International Conference on Computer Vision (ICCV). IEEE, 2011, pp. 2320–2327.
[15] R. Roberts, H. Nguyen, N. Krishnamurthi, and T. Balch, “Memory-based learning for visual odometry,” in Proceedings of IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2008, pp. 47–52.
[16] V. Guizilini and F. Ramos, “Semi-parametric learning for visual odometry,” The International Journal of Robotics Research, vol. 32, no. 5, pp. 526–546, 2013.
[17] T. A. Ciarfuglia, G. Costante, P. Valigi, and E. Ricci, “Evaluation of non-geometric methods for visual odometry,” Robotics and Autonomous Systems, vol. 62, no. 12, pp. 1717–1730, 2014.
[18] N. Su ̈nderhauf, S. Shirazi, A. Jacobson, F. Dayoub, E. Pepperell, B. Upcroft, and M. Milford, “Place recognition with convnet landmarks: Viewpoint-robust, condition-robust, training-free,” in Proceedings of Robotics: Science and Systems (RSS), 2015.
[20] A. Kendall, M. Grimes, and R. Cipolla, “Convolutional networks for real-time 6-DoF camera relocalization,” in Proceedings of International Conference on Computer Vision (ICCV), 2015.
[21] G. Costante, M. Mancini, P. Valigi, and T. A. Ciarfuglia, “Exploring representation learning with CNNs for frame-to-frame ego-motion estimation,” IEEE Robotics and Automation Letters, vol. 1, no. 1, pp.18–25, 2016.
[24] A. Dosovitskiy, P. Fischery, E. Ilg, C. Hazirbas, V. Golkov, P. van der Smagt, D. Cremers, T. Brox et al., “Flownet: Learning optical flow with convolutional networks,” in Proceedings of IEEE International Conference on Computer Vision (ICCV). IEEE, 2015, pp. 2758–2766.