DREAM TO CONTROL: LEARNING BEHAVIORS BY LATENT IMAGINATION
Presented by
Bowen You
Introduction
Reinforcement learning refers to training a neural network to make a series of decisions dependent on a complex, evolving environment. Typically, this is accomplished by 'rewarding' or 'penalizing' the network based on its behaviors over time. Intelligent agents are able to
In the general reinforcement learning framework, one typically trains an agent to learn complex behaviors. Intelligent agents are able to accomplish complex tasks that have never been seen in prior experience. One way to achieve this is by building a representation of the world based on past experiences. The authors propose an agent that learns long-horizon behaviors purely by latent imagination and outperforms previous agents in terms of data efficiency, computation time, and final performance.
Preliminaries
This section aims to define a few key concepts in reinforcement learning. In the typical reinforcement problem, an agent interacts with the environment. The environment is typically defined by a model that may or may not be known. The environment may be characterized by its state [math]\displaystyle{ s \in \mathcal{S} }[/math]. The agent may choose to take actions [math]\displaystyle{ a \in \mathcal{A} }[/math] to interact with the environment. Once an action is taken, the environment returns a reward [math]\displaystyle{ r \in \mathcal{R} }[/math]as feedback.
The actions an agent decides to take is defined by a policy function [math]\displaystyle{ \pi : \mathcal{S} \to \mathcal{A} }[/math]. Additionally we define functions [math]\displaystyle{ V_{\pi} : \mathcal{S} \to \mathbb{R} \in \mathcal{S} }[/math] and [math]\displaystyle{ Q_{\pi} : \mathcal{S} \times \mathcal{A} \to \mathbb{R} }[/math] to represent the value function and action-value functions of a given policy [math]\displaystyle{ \pi }[/math] respectively.
Thus the goal is to find an optimal policy [math]\displaystyle{ \pi_{*} }[/math] such that \[ \pi_{*} = \arg\max_{\pi} V_{\pi}(s) = \arg\max_{\pi} Q_{\pi}(s, a) \]
Feedback Loop
Given this framework, agents are able to interact with the environment in a sequential fashion, namely a sequence of actions, states, and rewards. Let [math]\displaystyle{ S_t, A_t, R_t }[/math] denote the state, action, and reward obtained at time [math]\displaystyle{ t = 1, 2, \ldots, T }[/math]. We call the tuple [math]\displaystyle{ (S_t, A_t, R_t) }[/math] one episode. This can be thought of as a feedback loop or a sequence \[ S_1, A_1, R_1, S_2, A_2, R_2, \ldots, S_T \]
Motivation
In many problems, the amount of actions an agent is able to take is limited. Then it is difficult to interact with the environment to learn an accurate representation of the world. The proposed method in this paper aims to solve this problem by "imagining" the state and reward that the action will provide. That is, given a state [math]\displaystyle{ S_t }[/math], the proposed method generates \[ \hat{A}_t, \hat{R}_t, \hat{S}_{t+1}, \ldots \]
By doing this, an agent is able to plan-ahead and perceive a representation of the environment without interacting with it. Once an action is made, the agent is able to update their representation of the world by the actual observation. This is particularly useful in applications where experience is not easily obtained.
Dreamer
The authors of the paper call their method Dreamer. It consists of:
- Representation [math]\displaystyle{ p_{\theta}(s_t | s_{t-1}, a_{t-1}, o_{t}) }[/math]
- Transition [math]\displaystyle{ q_{\theta}(s_t | s_{t-1}, a_{t-1}) }[/math]
- Reward [math]\displaystyle{ q_{\theta}(r_t | s_t) }[/math]
- Action [math]\displaystyle{ q_{\phi}(a_t | s_t) }[/math]
- Value [math]\displaystyle{ v_{\psi}(s_t) }[/math]
where [math]\displaystyle{ \theta, \phi, \psi }[/math] are learned neural network parameters.
There are three main components to the proposed algorithm:
- Dynamics Learning: Using past experience data, the agent learns to encode observations and actions into latent states and predicts environment rewards. One way to do this is via representation learning.
- Behavior Learning: In the latent space, the agent predicts state values and actions that maximize the future rewards through back-propagation.
- Environment Interaction: The agent encodes the episode to compute the current model state and predict the next action to interact with the environment.
The proposed algorithm is described below.
Notice that there are three neural networks that are trained simultaneously. The neural networks with parameters [math]\displaystyle{ \theta, \phi, \psi }[/math] correspond to models of the environment, action and values respectively.
Results
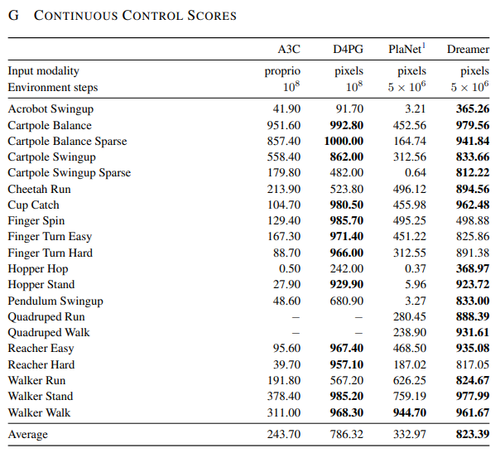
The figure below summarizes the performance of Dreamer compared to other state-of-the-art reinforcement learning agents for continuous control tasks. Overall, it achieves the most consistent performance among them. Additionally, while other agents heavily rely on prior experience, Dreamer is able to learn behaviors with minimal interactions with the environment.
Conclusion
This paper presented a new algorithm for training reinforcement learning agents with minimal interactions with the environment. The algorithm outperforms many previous algorithms in terms of computation time and overall performance. This has many practical applications as many agents rely on prior experience which may be hard to obtain in the real-world. Although it may be an extreme example, consider a reinforcement learning agent that learns how to perform rare surgeries may not have enough data samples. This paper shows that it is possible to train agents without requiring many prior interactions with the environment.
References
[1] D. Hafner, T. Lillicrap, J. Ba, and M. Norouzi. Dream to control: Learning behaviors by latent imagination. In International Conference on Learning Representations (ICLR), 2020.
[2] R. S. Sutton and A. G. Barto. Reinforcement learning: An introduction. MIT press, 2018.