DREAM TO CONTROL: LEARNING BEHAVIORS BY LATENT IMAGINATION
Presented by
Bowen You
Introduction
Reinforcement learning (RL) is one of the three basic machine learning paradigms, alongside supervised and unsupervised learning. It refers to training a neural network to make a series of decisions dependent on a complex, evolving environment. Typically, this is accomplished by 'rewarding' or 'penalizing' the network based on its behavior over time. Intelligent agents are able to accomplish tasks that may not have been seen in prior experiences. For recent reviews of reinforcement learning, see [3,4]. One way to achieve this is to represent the world based on past experiences. In this paper, the authors propose an agent that learns long-horizon behaviors purely by latent imagination and outperforms previous agents in terms of data efficiency, computation time, and final performance. Along with the latent space representation, an actor-critic model is used to learn the reaction and optimize the behavior of the agent. The proposed method is based on model-free RL with latent state representation that is learned via prediction. The term "model-free" in RL refers to not having an explicit model of the environment and its dynamics - there is still a model of the agent being learned. The authors have changed the belief representations to learn a critic, or value function, directly on latent state samples which help to enable scaling to more complex tasks.
The main finding of the paper is that long-horizon behaviors can be learned by latent imagination. This avoids the short sightedness that comes with using finite imagination horizons. The authors have also managed to demonstrate empirical performance for visual control by evaluating the model on image inputs.

Preliminaries
This section aims to define a few key concepts in reinforcement learning. In the typical reinforcement problem, an agent interacts with the environment. The environment is typically defined by a model that may or may not be known. The environment may be characterized by its state [math]\displaystyle{ s \in \mathcal{S} }[/math]. The agent may choose to take actions [math]\displaystyle{ a \in \mathcal{A} }[/math] to interact with the environment. Once an action is taken, the environment returns a reward [math]\displaystyle{ r \in \mathcal{R} }[/math] as feedback.
The actions an agent decides to take is defined by a policy function [math]\displaystyle{ \pi : \mathcal{S} \to \mathcal{A} }[/math]. Additionally we define functions [math]\displaystyle{ V_{\pi} : \mathcal{S} \to \mathbb{R} \in \mathcal{S} }[/math] and [math]\displaystyle{ Q_{\pi} : \mathcal{S} \times \mathcal{A} \to \mathbb{R} }[/math] to represent the value function and action-value functions of a given policy [math]\displaystyle{ \pi }[/math] respectively. Informally, [math]\displaystyle{ V_{\pi} }[/math] tells one how good a state is in terms of the expected return when starting in the state [math]\displaystyle{ s }[/math] and then following the policy [math]\displaystyle{ \pi }[/math]. Similarly [math]\displaystyle{ Q_{\pi} }[/math] gives the value of the expected return starting from the state [math]\displaystyle{ s }[/math], taking the action [math]\displaystyle{ a }[/math], and subsequently following the policy [math]\displaystyle{ \pi }[/math].
Thus the goal is to find an optimal policy [math]\displaystyle{ \pi_{*} }[/math] such that \[ \pi_{*} = \arg\max_{\pi} V_{\pi}(s) = \arg\max_{\pi} Q_{\pi}(s, a) \]
Feedback Loop
Given this framework, agents are able to interact with the environment in a sequential fashion, namely a sequence of actions, states, and rewards. Let [math]\displaystyle{ S_t, A_t, R_t }[/math] denote the state, action, and reward obtained at time [math]\displaystyle{ t = 1, 2, \ldots, T }[/math]. We call the tuple [math]\displaystyle{ (S_t, A_t, R_t) }[/math] one episode. This can be thought of as a feedback loop or a sequence \[ S_1, A_1, R_1, S_2, A_2, R_2, \ldots, S_T \]
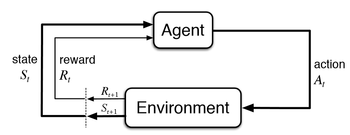
Motivation
In many problems, the amount of actions an agent is able to take while learning is limited, for example due to computational resource limitations, sensitivity of the environment, or physical resource constraints. Thus, it is difficult to sufficiently interact with the environment until an accurate representation of the world is learned. The proposed method in this paper aims to solve this problem by "imagining" the states and rewards that an action will provide. That is, given a state [math]\displaystyle{ S_t }[/math], the proposed method generates \[ \hat{A}_t, \hat{R}_t, \hat{S}_{t+1}, \ldots \]
By doing this, an agent is able to plan-ahead and perceive a representation of the environment without interacting with it. Once an action is made, the agent is able to update their representation of the world with the actual observation. This is particularly useful in applications where experience is not easily obtained.
Dreamer
The authors of the paper call their method Dreamer. From a high-level perspective, Dreamer first learns latent dynamics from past experience. Then it learns actions and states from imagined trajectories to maximize future action rewards. Finally, it predicts the next action and executes it. This whole process is illustrated below.
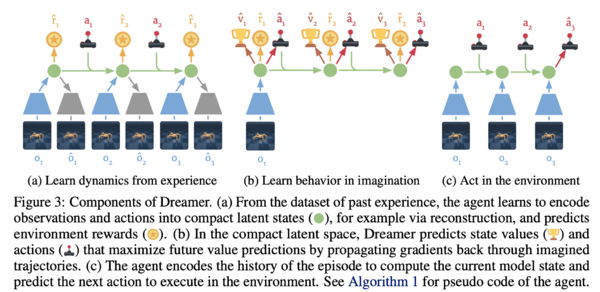
Let's look at Dreamer in detail. It consists of :
- Representation [math]\displaystyle{ p_{\theta}(s_t | s_{t-1}, a_{t-1}, o_{t}) }[/math]
- Transition [math]\displaystyle{ q_{\theta}(s_t | s_{t-1}, a_{t-1}) }[/math]
- Reward [math]\displaystyle{ q_{\theta}(r_t | s_t) }[/math]
- Action [math]\displaystyle{ q_{\phi}(a_t | s_t) }[/math]
- Value [math]\displaystyle{ v_{\psi}(s_t) }[/math]
where [math]\displaystyle{ o_{t} }[/math] is the observation at time [math]\displaystyle{ t }[/math] and [math]\displaystyle{ \theta, \phi, \psi }[/math] are learned neural network parameters.
The main three components of agent learning in imagination are dynamics learning, behaviour learning, and environment interaction. In the compact latent space of the world model, the behaviour is learned by predicting hypothetical trajectories. Throughout the agent's lifetime, Dreamer performs the following operations either in parallel or interleaved as shown in Figure 3 and Algorithm 1:
- Dynamics Learning: Using past experience data, the agent learns to encode observations and actions into latent states and predicts environment rewards. One way to do this is via representation learning.
- Behaviour Learning: In the latent space, the agent predicts state values and actions that maximize future rewards through back-propagation.
- Environment Interaction: The agent encodes the episode to compute the current model state and predict the next action to interact with the environment.
The proposed algorithm is described below.

Notice that three neural networks are trained simultaneously. The neural networks with parameters [math]\displaystyle{ \theta, \phi, \psi }[/math] correspond to models of the environment, action and values respectively. The action model tries to solve the imagination environment by predicting various actions. Meanwhile, the value model estimates the expected rewards that the action model will achieve. Hence, these two models are trained cooperatively whereby the action model tries to maximize the estimated value while the value model gives the estimate based on the action model's actions.
The Markovianity Question
The paper formulates visual control as a so-called Partially Observable Markov Decision Processs (POMDP) in discrete time. Since the goal is for an agent to maximize its sum of rewards in a Markovian setting, this puts the model squarely in the category of reinforcement learning. In this subsection we provide a lengthier discussion on this Markovian assumption.
Note that the transition distribution provided in the representation and transition models are Markovian in the states [math]\displaystyle{ s_t }[/math] and [math]\displaystyle{ a_t }[/math]. This mimics the dynamics in a non-linear Kalman filter and hidden Markov models. These techniques are described in the papers by Rabiner and Juang [5] as well as Kalman [6]. The difference with these presentations is that the latent dynamics are conditioned on actions and attempts to predict rewards, which allows the agent to imagine, yet not execute, actions in the provided environment.
This short memory assumption is useful from a computational perspective as it allows for the problem to be tractable. It is also realistic, as an intelligent agent does not need the entire history of their environment going back all the way to the Big Bang to understand a situation they have not encountered before. We commend the team at UofT and Google Brain for this insight, as it makes their analysis reasonable and easy to understand.
Related Works
Previous Works that exploited latent dynamics can be grouped in 3 sections:
- Visual Control with latent dynamics by derivative-free policy learning or online planning.
- Augment model-free agents with multi-step predictions.
- Use analytic gradients of Q-values.
While the later approaches are often for low-dimensional tasks, Dreamer uses analytic gradients to efficiently learn long-horizon behaviours for visual control purely by latent imagination.
Results
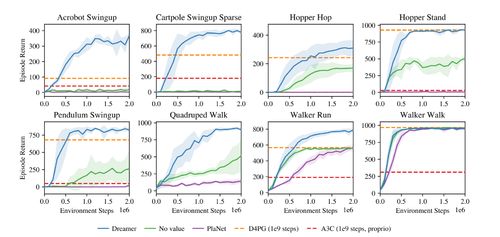
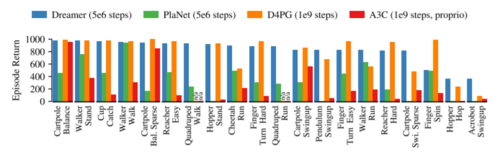
The experiments were performed on 20 different control tasks of Deepmind Control Suite [7]. In the following picture we can see the reward vs the environment steps for a few of the experiments. As we can see the Dreamer outperforms other baseline algorithms. Moreover, the convergence is a lot faster in the Dreamer algorithm.
The figure below summarizes Dreamer's performance compared to other state-of-the-art reinforcement learning agents for continuous control tasks. Using the same hyper parameters for all tasks, Dreamer exceeds previous model-based and model-free agents in terms of data-efficiency, computation time, and final performance. Overall, it achieves the most consistent performance among competing algorithms. Additionally, while other agents heavily rely on prior experience, Dreamer is able to learn behaviours with minimal interactions with the environment.
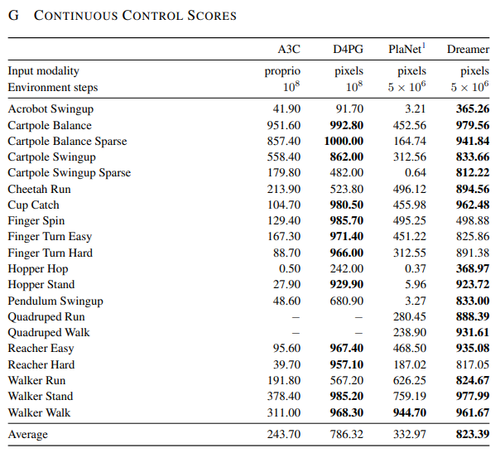
The performance is of Dreamer is also evaluated against state of the art reinforcement learning agents, which is shown below
Conclusion
This paper presented a new algorithm for training reinforcement learning agents with minimal interactions with the environment. The algorithm outperforms many previous algorithms in terms of computation time and overall performance. This has many practical applications as many agents rely on prior experience which may be hard to obtain in the real-world. For example, consider a reinforcement learning agent who learns how to perform rare surgeries without enough data samples. This paper shows that it is possible to train agents without requiring many prior interactions with the environment.
As future work on representation learning, the ability to scale latent imagination to higher visual complexity environments can be investigated.
Source Code
The code for this paper is freely available at https://github.com/google-research/dreamer.
Critique
This paper presents an approach that involves learning a latent dynamics model to learn 20 visual control tasks.
The model components in Appendix A have mentioned that "three dense layers of size 300 with ELU activations" and "30-dimensional diagonal Gaussians" have been used for distributions in latent space. The paper would have benefitted from pointing out how come they have come up with this architecture as their model. In other words, how the latent vector determines the performance of the agent.
Another fact about Dreamer is that it learns long-horizon behaviours purely by latent imagination, unlike previous approaches. It is also applicable to tasks with discrete actions and early episode termination.
Learning a policy from visual inputs is a quite interesting research approach in RL. This paper steps in this direction by improving existing model-based methods (the world models and PlaNet) using the actor-critic approach. However, their method was an incremental contribution as back-propagating gradients through values and dynamics has been studied in previous works.
References
[1] D. Hafner, T. Lillicrap, J. Ba, and M. Norouzi. Dream to control: Learning behaviours by latent imagination. In International Conference on Learning Representations (ICLR), 2020.
[2] R. S. Sutton and A. G. Barto. Reinforcement learning: An introduction. MIT press, 2018.
[3] Arulkumaran, K., Deisenroth, M. P., Brundage, M., & Bharath, A. A. (2017). Deep reinforcement learning: A brief survey. IEEE Signal Processing Magazine, 34(6), 26–38.
[4] Nian, R., Liu, J., & Huang, B. (2020). A review On reinforcement learning: Introduction and applications in industrial process control. Computers and Chemical Engineering, 139, 106886.
[5] Rabiner, Lawrence, and B. Juang. "An introduction to hidden Markov models." IEEE ASSP magazine 3.1 (1986): 4-16.
[6] Kalman, Rudolph Emil. "A new approach to linear filtering and prediction problems." (1960): 35-45.
[7] Y. Tassa, Y. Doron, A. Muldal, T. Erez, Y. Li, D. d. L. Casas, D. Budden, A. Abdolmaleki, J. Merel, A. Lefrancq, et al. Deepmind control suite. arXiv preprint arXiv:1801.00690, 2018.