compressive Sensing
Introduction
Faithfully and efficiently constructing a signal from a coded signal is an age old scientific problem. The Shannon/Nyquist sampling theorem states that in order to reconstruct a signal from a sampled signal without incurring artifacts such as aliasing, it is necessary to sample at least two times faster than the maximum signal bandwidth. However, in many applications such as digital image and video cameras, the Nyquist rate will result in an excessive number of samples, and making compression becomes a necessity before any storage or transmission of the samples can be made. Furthermore, in other applications such as medical scanners and radar, it is usually too costly to increase the sampling rate. This strict, and often costly, Nyquist criterion motivates a need for alternative methods. Compressive sensing, which is outlined in this paper summary, is one such approach that avoids the use of a high sampling rate for capturing signals.
Compressive sensing is a method of capturing and representing compressible signals at a rate significantly below the Nyquist rate. This method employs nonadaptive linear projections that maintain the structure of the signal, which is then reconstructed using the optimization techniques outlined in <ref name="R1"> C. Dick, F. Harris, and M. Rice, “Synchronization in software defined radios—Carrier and timing recovery using FPGAs,” in Proc. IEEE Symp. Field-Programmable Custom Computing Machines, NapaValley, CA, pp. 195–204, Apr. 2000.</ref> <ref name="R2">J. Valls, T. Sansaloni, A. Perez-Pascual, V. Torres, and V. Almenar, “The use of CORDIC in software defined radios: A tutorial,” IEEE Commun. Mag., vol. 44, no. 9, pp. 46–50, Sept. 2006.</ref>.
In summary, in this paper we will learn the definition of compressible signal, how to construct a compressible signal and then how to reconstruct the compressed signal.
Compressible Signals
Let us define a discrete time signal [math]\displaystyle{ \ x }[/math] such that it has following properties:
- Real valued
- Finite length
- One dimensional
Then [math]\displaystyle{ \ x }[/math] is a [math]\displaystyle{ N \times 1 }[/math] column vector in [math]\displaystyle{ \mathbb{R}^n }[/math] with elements [math]\displaystyle{ x[n], \; n=1,2,....N }[/math]. Note that an image or any other high-dimensional data point is pre-processed by first representing it as a long one-dimensional vector. To define a signal in [math]\displaystyle{ \mathbb{R}^n }[/math] we define the [math]\displaystyle{ N \times 1 }[/math] basis vectors [math]\displaystyle{ \, {\psi_i}, i = 1,\dots,n }[/math]. To keep it simple, assume that the basis is orthonormal. Using a [math]\displaystyle{ N \times N }[/math] basis matrix [math]\displaystyle{ \,\psi = [\psi_1|\psi_2|......|\psi_N] }[/math], the signal [math]\displaystyle{ \ x }[/math] can be expressed as
where [math]\displaystyle{ \ s }[/math] is a [math]\displaystyle{ N \times 1 }[/math] column vector of weighting coefficients [math]\displaystyle{ s_i=\langle x,\psi_i \rangle=\psi^{T}_i x }[/math].
It is easy to see that both [math]\displaystyle{ \,x }[/math] and [math]\displaystyle{ \,s }[/math] are equivalent representations of
the given signal that is to be captured, with [math]\displaystyle{ \,x }[/math] being in the time or space domain (depending on the nature of the signal)
and [math]\displaystyle{ \,s }[/math] being in the [math]\displaystyle{ \,\psi }[/math] domain. The signal is [math]\displaystyle{ \ K }[/math]-sparse if it is a linear combination of only [math]\displaystyle{ \ K }[/math] basis vectors. The signal will be compressible if the above representation has just a few large coefficients and many small coefficients. We shall now briefly overview how the transform coding of signals that uses a sample-then-compress
framework is done in data acquisition systems such as digital cameras (for which transform coding plays a central role). The procedure of this type of transform coding can be described in the following steps:
- Step 1: The full [math]\displaystyle{ \,N }[/math]-sample signal [math]\displaystyle{ x }[/math] is acquired.
- Step 2: The complete set of transform coefficients [math]\displaystyle{ \,{si} }[/math] is computed via [math]\displaystyle{ \,s = \psi^T x }[/math].
- Step 3: The [math]\displaystyle{ \,K }[/math] largest coefficients are located.
- Step 4: The [math]\displaystyle{ \,(N }[/math] − [math]\displaystyle{ \,K) }[/math] smallest coefficients are discarded.
- Step 5: The [math]\displaystyle{ \,K }[/math] values and locations of the largest coefficients are encoded.
Please note that the transform coding that uses a sample-then-compress framework has the following inherent inefficiencies:
- The initial number of samples [math]\displaystyle{ \,N }[/math] may be very large even if the desired [math]\displaystyle{ \ K }[/math] is small.
- The set of all [math]\displaystyle{ \ N }[/math] transform coefficients [math]\displaystyle{ \ {s_i} }[/math] must be calculated even though all but [math]\displaystyle{ \ K }[/math] of them will be discarded.
- The locations of the large coefficients must be encoded, thus introducing an overhead to the algorithm.
The Problem Statement for the Compressive Sensing Problem
Compressive sensing directly acquires the compressed signal without going through the intermediate stage of acquiring [math]\displaystyle{ \ N }[/math] samples. In order to do this, a general linear measurement process is defined such that [math]\displaystyle{ \, M \lt N }[/math] inner products between [math]\displaystyle{ \ x }[/math] and a collection of vectors [math]\displaystyle{ \{\phi \}_{j=1}^M }[/math] are computed to give [math]\displaystyle{ y_{j}=\langle x, \phi_j \rangle }[/math].
Ordering the new measurement vectors [math]\displaystyle{ \ y_j }[/math] in a [math]\displaystyle{ M\times 1 }[/math] vector [math]\displaystyle{ \ y }[/math], and the measurement vectors [math]\displaystyle{ \phi_{j}^{T} }[/math] as rows in an [math]\displaystyle{ M \times N }[/math] matrix [math]\displaystyle{ \ \phi }[/math], we can then use [math]\displaystyle{ \ x=\psi s }[/math] to get
where [math]\displaystyle{ \ \theta=\phi \psi }[/math] is an [math]\displaystyle{ M \times N }[/math] matrix. This measurement process is nonadaptive, which implies that [math]\displaystyle{ \ \phi }[/math] is fixed and does not depend on the signal [math]\displaystyle{ \ x }[/math]. So, in order to design a viable compressive sensing method the following two conditions must be met:
- A stable measurement matrix [math]\displaystyle{ \ \phi }[/math] must be constructed which preserves the information while reducing the dimension from [math]\displaystyle{ \ N }[/math] to [math]\displaystyle{ \ M }[/math].
- A reconstructing algorithm must be designed which recovers [math]\displaystyle{ \ x }[/math] from [math]\displaystyle{ \ y }[/math] by using only [math]\displaystyle{ M \approx K }[/math] measurements (which is roughly the number of coefficients recorded by the traditional transform coder mentioned earlier).
Part 1 of the Solution: Constructing a Stable Measurement Matrix
Given the [math]\displaystyle{ \, M }[/math] available measurements, [math]\displaystyle{ \, y }[/math], where [math]\displaystyle{ \,M \lt N }[/math],[math]\displaystyle{ \,\phi }[/math] must be able to reconstruct the signal [math]\displaystyle{ \, x }[/math] with a high level of accuracy. If [math]\displaystyle{ \,x }[/math] is [math]\displaystyle{ \,K }[/math]-sparse and the locations of the non-zero coefficients in [math]\displaystyle{ \,s }[/math] is known, then the problem can be solved provided [math]\displaystyle{ M \geq K }[/math]. For this problem to be well conditioned we must have the following necessary and sufficient condition.
where [math]\displaystyle{ \,v }[/math] is a vector sharing the same non-zero entries as [math]\displaystyle{ \,s }[/math] and [math]\displaystyle{ \epsilon \geq 0 }[/math], and where [math]\displaystyle{ \epsilon }[/math] is the restrictive isometry constant. This means [math]\displaystyle{ \,\theta }[/math] must preserve the lengths of these particular K-sparse vectors. This condition is referred to as the restricted isometry property (RIP)<ref name="R1"> C. Dick, F. Harris, and M. Rice, “Synchronization in software defined radios—Carrier and timing recovery using FPGAs,” in Proc. IEEE Symp. Field-Programmable Custom Computing Machines, NapaValley, CA, pp. 195–204, Apr. 2000.</ref> <ref name="R2">J. Valls, T. Sansaloni, A. Perez-Pascual, V. Torres, and V. Almenar, “The use of CORDIC in software defined radios: A tutorial,” IEEE Commun. Mag., vol. 44, no. 9, pp. 46–50, Sept. 2006.</ref>. Note that, in practice, it is typically impossible to known the locations of the [math]\displaystyle{ \,K }[/math] non-zero entries in [math]\displaystyle{ \,s }[/math]. However, a sufficient condition for a stable solution for both K-sparse signals and compressible signals is that [math]\displaystyle{ \,\theta }[/math] satisfies the RIP for an arbitrary [math]\displaystyle{ \,3K }[/math]-sparse vector [math]\displaystyle{ \,v }[/math]. A similar property to the RIP called incoherence requires that the rows [math]\displaystyle{ \,\{\phi_j\} }[/math] of [math]\displaystyle{ \,\phi }[/math] cannot sparsely represent the columns [math]\displaystyle{ \,\{\psi_i\} }[/math] of [math]\displaystyle{ \,\psi }[/math], and vice versa. Consequently, both [math]\displaystyle{ \,K }[/math]-sparse signals and compressible signals of length [math]\displaystyle{ \,N }[/math] can be reconstructed using only [math]\displaystyle{ \,M \ge cK log(N/K) \lt \lt N }[/math] random Gaussian measurements.
The RIP and incoherence conditions can be satisfied with high probability simply by choosing a random matrix, [math]\displaystyle{ \,\phi }[/math]. For example, let us construct a matrix [math]\displaystyle{ \,\phi }[/math] such that its matrix elements [math]\displaystyle{ \,\phi_{i,j} }[/math] are independent and identically distributed (iid) random variables from a Gaussian probability distribution with mean zero and variance [math]\displaystyle{ \,1/N }[/math] <ref name="R1"/><ref name="R2"/><ref name="R4> R.G. Baraniuk, M. Davenport, R. DeVore, and M.D. Wakin, "A simples proof of the restricted isometry principle for random matrices (aka the Johnson-Linstrauss lemma meets compressed sensing)," Constructive Approximation, 2007.</ref>. Then, the measurements [math]\displaystyle{ \,y }[/math] are merely [math]\displaystyle{ \,M }[/math] different randomly weighted linear combinations of the elements of [math]\displaystyle{ \,x }[/math] and the Gaussian measurement matrix [math]\displaystyle{ \,\phi }[/math] has the following properties:
- The incoherence property is satisfied by the matrix [math]\displaystyle{ \,\phi }[/math] with the basis [math]\displaystyle{ \,\psi = I }[/math] with high probability since it is unlikely that the rows of the Gaussian matrix [math]\displaystyle{ \,\phi }[/math] will sparsely represent the columns of the identity matrix and vice versa. In this case, if [math]\displaystyle{ \, M \geq cK\log(N/K) }[/math] with [math]\displaystyle{ \,c }[/math] a small constant, then [math]\displaystyle{ \,\theta = \phi\psi = \phi I = \phi }[/math] will satisfy the RIP with high probability.
- The matrix [math]\displaystyle{ \,\phi }[/math] is universal, meaning that [math]\displaystyle{ \,\theta }[/math] will satisfy the RIP with high probability regardless of the choice of the orthonormal basis [math]\displaystyle{ \,\psi }[/math].
Part 2 of the Solution: Designing a Reconstruction Algorithm for Signals
Now we are left with the task of designing a reconstruction algorithm. The reconstruction algorithm must take into account the [math]\displaystyle{ \,M }[/math] measurements in the vector [math]\displaystyle{ \,y }[/math], the random measurement matrix [math]\displaystyle{ \,\phi }[/math] (or the seed that was used to generate it) and the basis [math]\displaystyle{ \,\psi }[/math] and then reconstruct the length [math]\displaystyle{ \,N }[/math] signal [math]\displaystyle{ \,x }[/math] or its sparse coefficient vector [math]\displaystyle{ \,s }[/math]. Since [math]\displaystyle{ \,M\lt N }[/math], the system is underdetermined (having fewer equations than variables), and thus we have infinitely many [math]\displaystyle{ \,s' }[/math] which satisfy
The justification for this is that if [math]\displaystyle{ \,\theta s=y }[/math] then [math]\displaystyle{ \,\theta (s+r)=y }[/math] for any vector [math]\displaystyle{ \,r }[/math] in the null space of [math]\displaystyle{ \,\theta }[/math], denoted [math]\displaystyle{ \,N(\theta) }[/math] . This suggests finding the signal's sparse coefficient vector in the [math]\displaystyle{ \,(N-M) }[/math] dimensional translated null space [math]\displaystyle{ \,H=N(\theta)+s }[/math]. Related to the concept of Lp space, the [math]\displaystyle{ \,l_p }[/math] norm of the vector [math]\displaystyle{ \,s }[/math] is [math]\displaystyle{ \,(||s||_p)^p = \sum_{i=1}^N |s_i|^p }[/math]. With this concept in mind, the reconstruction process can be attempted in the following ways that make use of the concept of [math]\displaystyle{ \,l_p }[/math] norm.
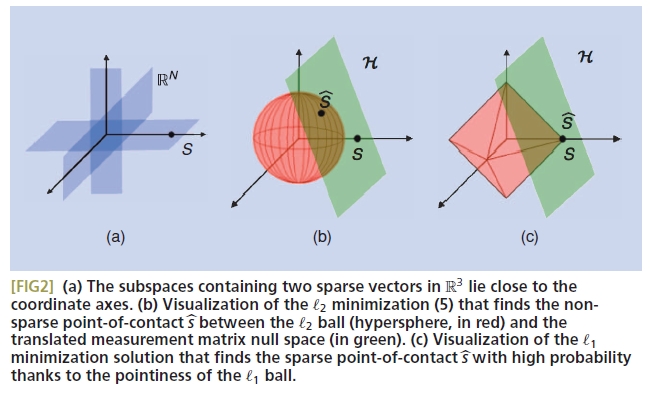
Minimum [math]\displaystyle{ \,l_2 }[/math] norm reconstruction
In order to find the vector [math]\displaystyle{ \,s }[/math], the classical approach is to find the vector in the transformed null space with the smallest [math]\displaystyle{ \,l_2 }[/math] norm (also called energy norm) by solving
The closed form solution is given by [math]\displaystyle{ \hat{s}=\theta^{T}(\theta \theta^{T})^{-1}y }[/math]. However, the minimization returns non-sparse [math]\displaystyle{ \hat{s} }[/math] with many non-zero elements. In other words, it is almost never able to reconstruct the original signal.
Minimum [math]\displaystyle{ \,l_0 }[/math] norm reconstruction
The drawback of using the [math]\displaystyle{ \,l_2 }[/math] norm in reconstruction is that the [math]\displaystyle{ \,l_2 }[/math] norm measures signal energy rather than signal sparsity. For reconstruction, the use of the [math]\displaystyle{ \,l_0 }[/math] norm is much more suitable, because the [math]\displaystyle{ \,l_0 }[/math] norm counts the number of non-zero entries in [math]\displaystyle{ \,s }[/math], i.e. the [math]\displaystyle{ \,l_0 }[/math] norm of a [math]\displaystyle{ \,K }[/math]-sparse vector is simply [math]\displaystyle{ \,K }[/math]. Let us now evaluate the [math]\displaystyle{ \,l_0 }[/math] norm, also known as the cardinality function (since it counts the number of non-zero entries in [math]\displaystyle{ \,s }[/math]). In this case the problem formulation is
At first glance this approach looks attractive since it recovers the K-sparse signal exactly with high probability using only [math]\displaystyle{ \,M = K+1 }[/math] i.i.d Gaussian measurements. However, solving the equation is numerically unstable and NP-complete which requires an exhaustive search of all [math]\displaystyle{ (_K^{N}) }[/math] possible locations of the non-zero entries in [math]\displaystyle{ \,s }[/math].
Minimum [math]\displaystyle{ \,l_1 }[/math] norm reconstruction
Now, if we perform minimization using the [math]\displaystyle{ \,l_1 }[/math] norm , we are able to recover [math]\displaystyle{ \,K }[/math]-sparse signals and closely approximate the compressible signal with high probability using only [math]\displaystyle{ M \geq cK\log(\frac{N}{K}) }[/math] i.i.d Gaussian measurements. We aim to solve
This optimization problem is convex and reduces to a linear program known as basis pursuit<ref name="R1"> C. Dick, F. Harris, and M. Rice, “Synchronization in software defined radios—Carrier and timing recovery using FPGAs,” in Proc. IEEE Symp. Field-Programmable Custom Computing Machines, NapaValley, CA, pp. 195–204, Apr. 2000.</ref> <ref name="R2">J. Valls, T. Sansaloni, A. Perez-Pascual, V. Torres, and V. Almenar, “The use of CORDIC in software defined radios: A tutorial,” IEEE Commun. Mag., vol. 44, no. 9, pp. 46–50, Sept. 2006.</ref>, and has computational complexity [math]\displaystyle{ \,O(N^3) }[/math].
Figure 2 from the original paper [5] illustrates these three approaches for reconstructing signals. For convenience, this figure is reproduced below.
Furthermore, other related reconstruction algorithms can be found in [6] and [7] of the original paper.
Example
The paper discusses a practical example of the technique of compressive sensing using a "single-pixel compressive sensing camera"<ref name = "R3"> D. Takhar, V. Bansal, M. Wakin, M. Duarte, D. Baron, J. Laska, K.F. Kelly, and R.G. Baraniuk, “A compressed sensing camera: New theory and an implementation using digital micromirrors,” in Proc. Comput. Imaging IV SPIE Electronic Imaging, San Jose, Jan. 2006.</ref>. The main idea is that the camera has a mirror for each pixel, and randomly, the mirror either reflects the light to something that can use it (a photodiode) or it doesn't. Thus, [math]\displaystyle{ \,y_i }[/math] is the voltage at each photodiode and as in the problem description, it is the inner product of the image we want, [math]\displaystyle{ \,x }[/math], and [math]\displaystyle{ \,\phi_i }[/math]. Here, [math]\displaystyle{ \,\phi_i }[/math] is a vector of ones and zeros, indicating whether mirrors direct light towards the photodiode or not. This can be repeated to get [math]\displaystyle{ \,y_1,\dots,y_M }[/math]. The image can be reconstructed using the techniques discussed. This example can be seen in the following diagram. The image in part (b) is from a conventional digital camera. The image in part (c) is constructed using the single-pixel camera. This method requires 60% fewer random measurements than reconstructed pixels.
Robustness
In practice, no measurement system is perfect---devices do not have infinite precision. Thus, it is necessary that compressed sensing continue to recover signals relatively well, even in the presence of noise. Fortunately, it has been shown that the error bound of compressive sensing is proportional to the error which results from the approximation to a sparse signal (the change of basis), plus the noise which is input to the system.
More formally,
where [math]\displaystyle{ \,x^* }[/math] is the signal recovered under noisy conditions, [math]\displaystyle{ \,x_s }[/math] is the vector [math]\displaystyle{ \,x }[/math] with all but the largest [math]\displaystyle{ \,S }[/math] components set to zero, and [math]\displaystyle{ \,\epsilon }[/math] is the error bound in the noise. Here, [math]\displaystyle{ \,C_0 }[/math] and [math]\displaystyle{ \,C_1 }[/math] are generally small.
This is a very important result, since it means that the noise produced by compressive sensing is directly proportional to the noise of the measurements. It is this result that ultimately moves compressive sensing from being an interesting academic exercise to something which is pragmatic.
Conclusion
The compressive sensing algorithm can be applied to analog signals as well. This sensing technique finds many practical applications in image processing and similar fields. In this summary, we learned about compressive sensing which is a more efficient method compared to the traditional transform coding of signals that uses a sample-then-compress framework.
References
<references />
5. Richard G. Baraniuk. Compressive Sensing.