Batch Normalization
2. Steps Towards Reducing Internal Covariate Shift
While normalizing the input will reduce training time and improve learning rates, after passing through fully connected layers of the neural network, the inputs are no longer normalized at each hidden layer. So, we want to reduce this internal covariate shift by normalizing the input at each hidden layer as well.
One traditional idea is to whiten the input data, by performing a transform involving the square root of the inverse of the Covariance matrix, to make the transformed data's covariance matrix equal to its identity. However, this is a very expensive operation, and does not necessarily lead to a gradient function that is well defined.
Another idea is to normalize the entire training set at each layer. However, this operation is also not effective, because the hidden layers will add a learned bias term b, such that x = u + b, and during the shifting of the mean, x - E[X] = u + b - E[u + b] = u - E[u]. Therefore, the learned bias term will be negated during the normalization phase.
What we need is a normalization technique that can be applied to each layer, yet can be learned; therefore it can respect the learned weights and biases of the previous layer.
3. Batch Normalization
The paper introduces a new technique known as Batch Normalization, which takes in a mini-batch of input of $d$ dimensional inputs, and produces a normalized minibatch of $d$ dimensional outputs. This operation is normally carried out before the activation function of a layer.
3.1 The BN Layer
Like the name suggests, the Batch Norm
4. Experiments
4.1 Training on a Simple Network
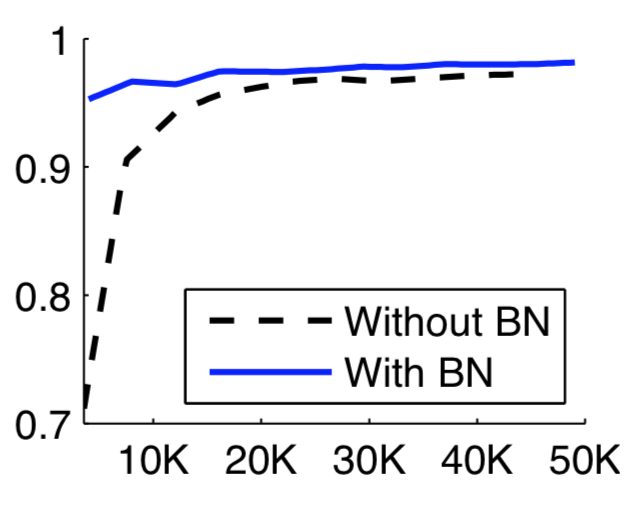
To test the effect of batch-normalization, the authors decided to monitor the training of two simple networks for the MNIST digit classification problem. The MNIST dataset consists of 28 by 28 images (60000 training images and 10000 testing images), where each image consists of a hand written digit. One network had the following architecture: an input layer which receives a flattened 28 by 28 image as input, three fully connected hidden layers with 100 nodes with the sigmoid nonlinearity, and an output layer with 10 nodes using the cross-entropy loss function. The other network had the same architecture with the exception of having batch-normalization layers right before the activations (to have the input to the activations be normalized as desired). Both networks were trained with 60 data points per mini-batch.
The following figure (x axis for number number of training points, y axis for accuracy) details the performance of the networks on validation data during training . The network using batch normalization achieved a higher accuracy far earlier into training, and converged much faster than the network without the normalization technique.
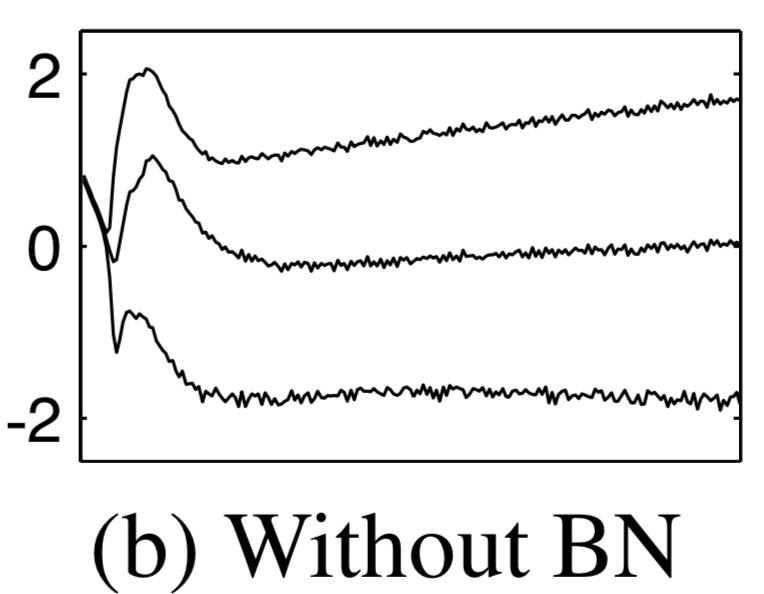
The input to the activation function of the last hidden layer was also studied during training. More specifically, the values corresponding to the 15th, 50th, and 85th percentiles of the input were recorded. The figure to the left demonstrates how these values changed during training. The y axis marks the values of the 15th, 50th and 85th percentile, while the x axis records the number of training points processing.
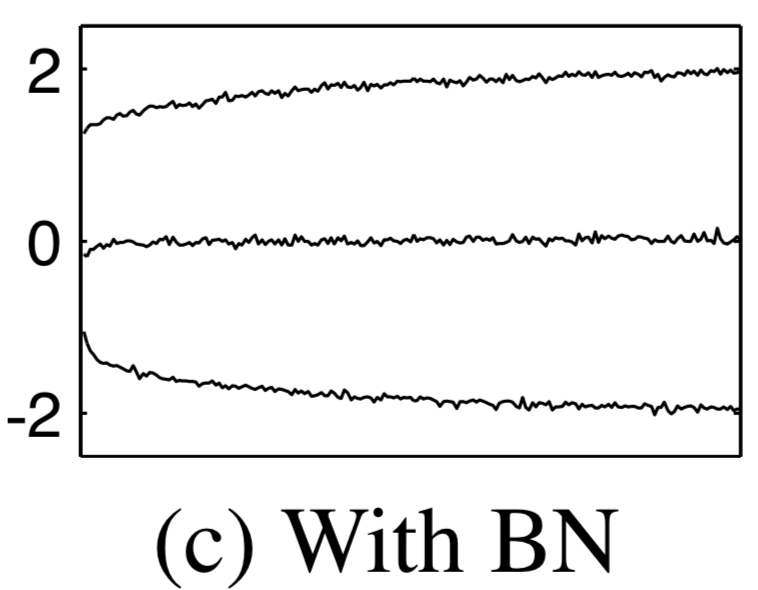
The same was done for the network trained using batch normalization. As we can see, the distribution of the input was much more stable throughout training (mean and variance changed less compared to the network trained without batch normalization) which the authors accredited to a reduction of internal covariate shift.
4.2 ImageNet Classification
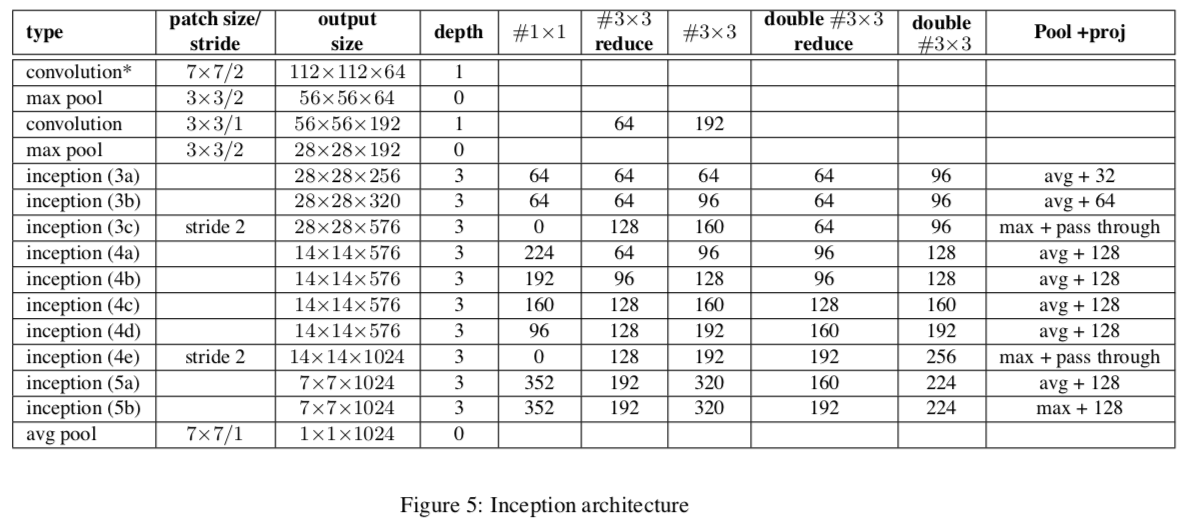
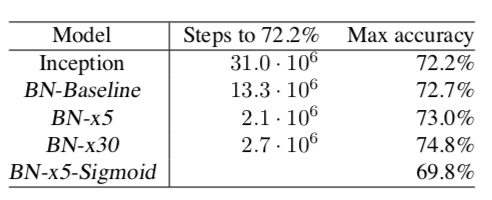
The ImageNet dataset one that is a lot more extensive than that of MNIST— it consists of just over 14 000 000 images of 1000 classes (ranging from animals to plants). The author’s decided to use Inception network as a baseline network with the adjustment of changing the convolution layers with 5 by 5 kernels to two consecutive convolution layers with 3 by 3 kernels (architecture outlined below). It’s worth pointing out that the Inception network employs ReLU as the nonlinearity. The authors decided to test 4 variations of this Inception network. The four varied models were BN-Baseline, BN-x5, BN-x30, BN-x5-sigmoid.
BN-Baseline was the same network as Inception except batch-normalization was introduced before the nonlinearities. BN-x5 is the same as BN-Baseline except the learning rate was increased to 0.0075 from 0.0015. BN-x30 used the learning rate of 0.045, 30 times more than that of BN-Baseline, and BN-x5-sigmoid is the same network as BN-x5 except it uses the sigmoid nonlinearity instead of ReLU. BN-x5-sigmoid did not perform well as a classifier, but the significance of this network is that networks with sigmoid nonlinearities were notoriously difficult to train (this same network without batch normalization had parameters which reached machine infinity)— batch-normalization enabled the use of saturating nonlinearities in deep neural networks.
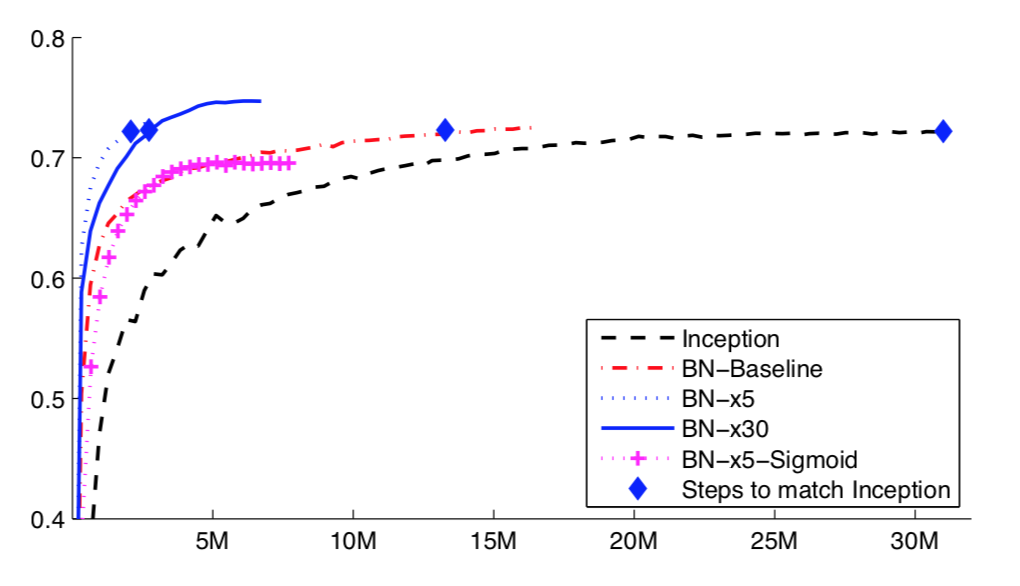
The performance of each network was recorded, as well as the number of training examples required to achieve the same accuracy as the baseline Inception network. Again, the BN-x5-sigmoid did not perform as well as the other models but marked a different achievement.
A more visual example to contrast how quickly the batch-normalized variants of Inception network achieved the same accuracy is as follows. It can be seen the variants were able to perform the same with 43% of the data (BN-Baseline), 6.7% of the data (BN-x5) and 8.7% (BN-x30).
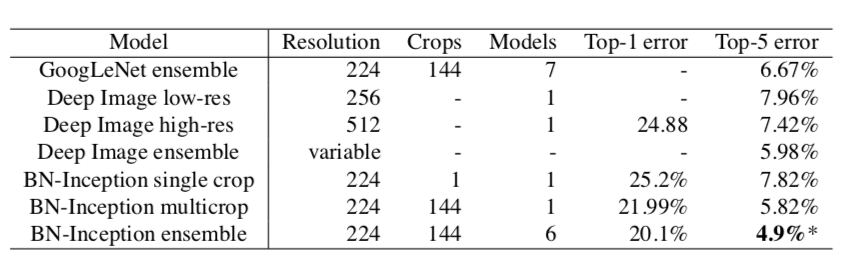
Ensemble networks demonstrated state of the art accuracy on the ImageNet challenge (compared to the standalone networks presented earlier), so training ensembles with batch-normalization was also investigated:
The authors were able to achieve the new state of the art accuracy using a slightly modified ensemble of six BN-x30 networks.