Augmix: New Data Augmentation method to increase the robustness of the algorithm
Presented by
Abhinav Chanana
Introduction
Often times machine learning algorithms assume that the training data is the correct representation of the data encountered during deployment. Algorithms generally ignore the chances of receiving little corruption which leads to less robustness and reduction in their accuracy as the models try to fit the noise for the predictions as well. A few corruptions have the potential to reduce the performance of various models like stated in the Hendrycks & Dietterich (2019), showing that the classification error rose from 25% to 62% when some corruption was introduced on the ImageNet test set. The problem with introducing some corruption is that it encourages the models or the network to memorize the specific corruptions and is, therefore, unable to generalize these corruptions. The paper also provides evidence that networks trained on translation augmentations are highly sensitive to the shifting of pixels. The paper comes with a new algorithm known as AugMix, a method which achieves new state-of-the-art results for robustness and uncertainty estimation while maintaining accuracy on standard benchmark datasets. The paper uses CIFAR 10, CIFAR100, ImageNet datasets for confirming the results. AUGMIX utilizes stochasticity and diverse augmentations, a Jensen-Shannon Divergence consistency loss, and a formulation to mix multiple augmented images to achieve state-of-the-art performance
Background
Data Augmentation helps to increase the size of the dataset by creating variations of existing images. This helps the model to generalize better, prevent overfitting and make the model more robust. Basic types of data augmentation techniques are Flipping, Rotation, Shearing, Cropping, etc. In the Flipping technique, the image is flipped horizontally or vertically. In the Rotation technique, the image is rotated by a certain degree, whereas, in the Cropping technique, a part of the image is removed to make the object appear in different proportions in different positions in the image.
Approach
At a high level, AugMix does some basic augmentations techniques. These augmentations are often layered to create a high diversity of augmented images. The loss is calculated using the Jensen-Shannon divergence method.

The method proposed by the author can be divided into 3 major sections:
1. Augmentations: The author uses basic data augmentation chains and the composition of data augmentation operations using AutoAugment. A chain is created like shown in the figure above
2. Mixing: The resulting images from these augmentation chains are combined by mixing. The author chose to use elementwise convex combinations for simplicity. The k-dimensional vector of convex coefficients is randomly sampled from a Dirichlet(α, . . . , α) distribution. The intuition behind using a Dirichlet distribution is that it allows us to sample coefficients from (0, 1) that sum to 1. Once these images are mixed, the author uses a “skip connection” to combine the result of the augmentation chain and the original image through a second random convex combination sampled from a Beta(α, α) distribution.
3. Jensen-Shannon divergence: The author augments the original loss function with the Jensen-Shannon divergence loss to enforce stable and consistent output: 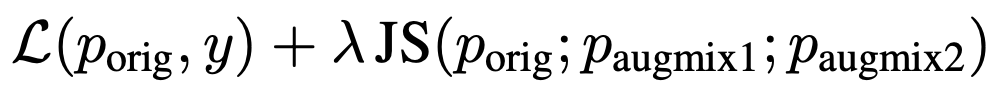
[math]\displaystyle{ p_\text{orig} }[/math], [math]\displaystyle{ p_\text{augmix1} }[/math] and [math]\displaystyle{ p_\text{augmix2} }[/math] are the posterior distributions of the original input [math]\displaystyle{ x_\text{orig} }[/math], and its augmented variants: [math]\displaystyle{ x_\text{augmix1}, x_\text{augmix2} }[/math], respectively.
The JS in the above formula means the Jensen-Shannon divergence. It measures the similarities between distributions and is based on KL divergence. However, the Jensen-Shannon divergence is symmetric and can be viewed as a smoothed and normalized version of KL divergence. The JS divergence is particularly helpful when we are comparing multiple distributions.
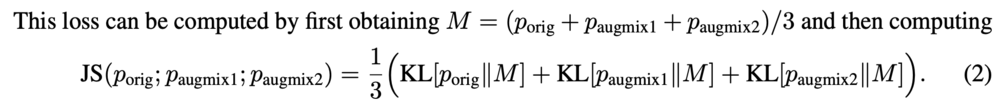
where KL means KL Divergence between porig and paugmix
The pseudocode for the algorithm:

For example, the pseudocode can be implemented in Python as follows:
import numpy as np
def augmix(orig_image, operations, k=3, alpha=1):
aug_image = np.zeros(orig_image.shape)
weights = np.random.dirichlet(np.ones(k)*alpha)
for i in range(k):
op1, op2, op3 = np.random.choice(operations, 3)
chain = np.random.uniform()
if 3*chain < 1:
aug_image += op1(orig_image)
elif 3*chain <2:
aug_image += op2(op1(orig_image))
else:
aug_image += op3(op2(op1(orig_image)))
m = np.random.beta(alpha, alpha)
augmix = m*orig_image + (1-m)*aug_image
return augmix
Data Set Used
The authors use the following datasets for conducting the experiment.
1. CIFAR 10: This dataset, along with the CIFAR-100 dataset, are labeled subsets of the 80 million tiny images dataset and were collected by Alex Krizhevsky, Vinod Nair, and Geoffrey Hinton. The CIFAR-10 dataset is composed of 60000 color images of 32x32 pixels. These images are in 10 classes, with 6000 images per class, 50000 for training, and 10000 for testing. This dataset is used in numerous computer vision journals to compare their algorithms. - https://www.cs.toronto.edu/~kriz/cifar.html
2. CIFAR 100: The difference between this dataset and the CIFAR-10 dataset is that it includes 100 classes of images with 600 images per each class. These classes are also grouped in 20 super-classes, e.g. the flowers' superclass that contains orchids, poppies, roses, sunflowers, and tulips. - https://www.cs.toronto.edu/~kriz/cifar.html
3. ImageNet: This dataset aims to obtain at least 1000 images per "synonym set" or "sysnet" in the WordNet hierarchy. WordNet is a large lexical database of English where nouns, verbs, adjectives and adverbs are grouped into sets of cognitive synonyms (synsets), each expressing a distinct concept. This dataset is currently home to 1.2 million labelled images. - http://image-net.org/download
Experiments
The author used CIFAR-10-C, CIFAR-100-C, and ImageNet-C datasets which are constructed by adding corruption to the original datasets. The CIFAR-10-P, CIFAR-100-P, and ImageNet-P datasets also modify the original CIFAR and ImageNet datasets. These datasets contain smaller perturbations than CIFAR-C and are used to measure the classifier’s prediction stability. The metrics used for comparison of the models is the error rate of the algorithm. The clean error is achieved by getting the error rates without applying any corruption of the datasets. In the experiment, the author uses 15 corruption techniques hence the error rate after corruption is taken as the average of all the error rates achieved by the specific model. In order to assess a model’s uncertainty estimates, we measure its miscalibration. The author uses Brier Score or d RMS Calibration Error for this purpose.
Results on CIFAR
For CIFAR datasets, 15 corruptions have been applied
Setup: The author has used three models for comparison: 1.A DenseNet-BC (k = 12, d = 100) 2.A 40-2 Wide ResNet 3.A ResNeXt-29 The All Convolutional Network and Wide ResNet train for 100 epochs, and the DenseNet and ResNeXt require 200 epochs for convergence and weight decay of 0.0001 for Mixup and 0.0005 otherwise.
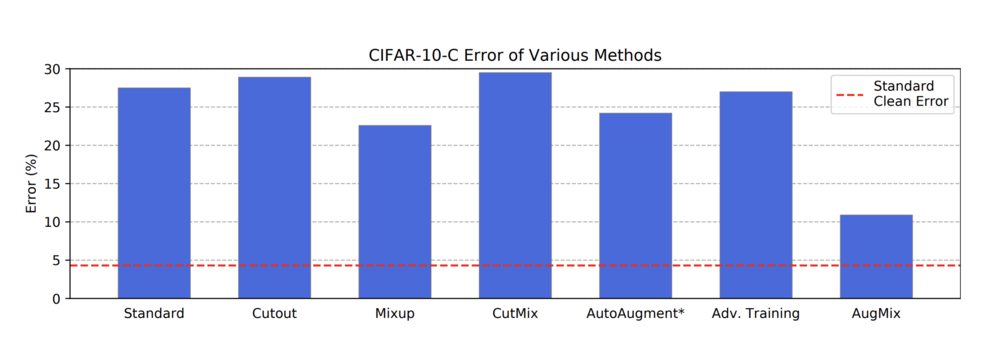
The author has further compared it to other state-of-the-art algorithms used for data augmentation, which can be seen in the above figure. The AugMix algorithm performs the best with a 16.6% lower absolute corruption error. This method only uses ResNeXt on CIFAR-10-C for comparison purposes.
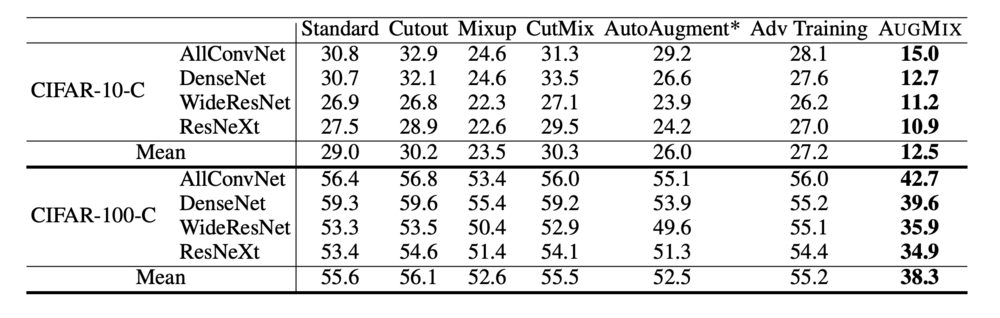
Results on ImageNet Dataset
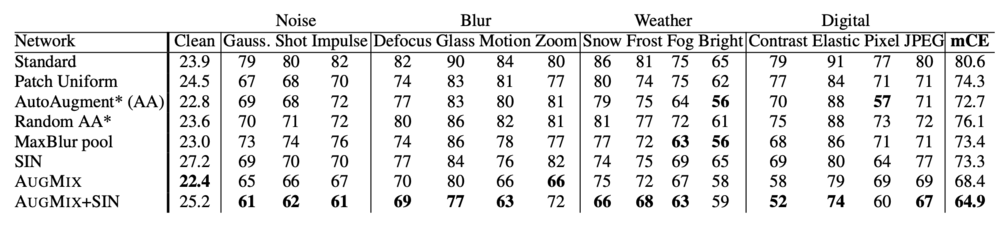
This shows Clean Error, Corruption Error (CE), and mCE values for various methods on ImageNet-C. The mCE value is computed by averaging across all 15 CE values. AUGMIX reduces corruption error while improving clean accuracy, and it can be combined with SIN for greater corruption robustness.
Source Code
The source code is available at: https://github.com/google-research/augmix
Conclusion
AUGMIX is a data processing technique that mixes randomly generated augmentations and uses a Jensen-Shannon loss to enforce consistency. The simple-to-implement technique obtains state-of-the-art performance on CIFAR and ImageNet.AUGMIX seems to enable more reliable models, a necessity for models deployed in safety-critical environments. Using AugMix with the above-specified models performs better and tolerant of corruption.
Critique
Since augmix1 and augmix2 are independent, why did they use JS divergence over the mixture of the three? What happened if they only used [math]\displaystyle{ \frac{1}{2} (KL(p_{orig},p_{augmix1})+KL(p_{orig}, p_{augmix2})) }[/math]. In other words, what is the priority of the JS over simple KL?
The authors considered a different type of noise to check the robustness of their approach. I would be really curious to test their methodology in Large Models, adding self-attention layers to models improves robustness. To test the abstraction properties, we know that the convolutional networks are biased towards texture, which might harm robustness. Another hypothesis on naturally occurring distribution shifts is the synthetic robustness interventions including diverse data augmentations which might not help with robustness.
Related Work
Recently, a lot of approaches to Mixed Sample Data Augmentation have been proposed, many of which obtain state-of-the-art performance in several classical classification tasks. The contribution of AugMix is to perform MixUp on highly augmented variations of a provided image. By the addition of a trick called Fast AutoAugment the authors of [1] claim they can beat the state-of-the-art (including beating AugMix) in the Fashion-MNIST dataset. What the authors do is apply a binary mask to low frequency images sampled from the Fourier space corresponding to the dataset. In particular, the mask arises from the following low-pass filter. Given a complex Gaussian random matrix [math]\displaystyle{ Z }[/math], and a decay power [math]\displaystyle{ \delta }[/math], we let: \begin{align} filter(z, \delta) [i,j] = \frac{z[i,j]}{freq(w,h) [i,j]^\delta} \end{align}
If [math]\displaystyle{ \mathcal{F}^{-1} }[/math] is the inverse discrete Fourier transform, we gray scale the image by setting:
\begin{align} G = Re (\mathcal{F}^{-1} (filter(Z, \delta )) ) \end{align}
Finally, this can be converted to a binary mask with mean [math]\displaystyle{ \lambda }[/math] on an image [math]\displaystyle{ g }[/math] by setting:
\begin{align} mask(\lambda , g)[i,j] = \chi_{ top(\lambda w h, g g) } \end{align}
Where [math]\displaystyle{ \chi }[/math] is the indicator function.
Bibliography
[1] Harris, E., Marcu, A., Painter, M., Niranjan, M., & Hare, A. P. B. J. (2020). Fmix: Enhancing mixed sample data augmentation. arXiv preprint arXiv:2002.12047, 3.