A Game Theoretic Approach to Class-wise Selective Rationalization: Difference between revisions
| Line 30: | Line 30: | ||
s.t. <math>g_0^f(\cdot)</math> and <math>g_0^c(\cdot)</math> satisfy some sparsity and continuity constraints. | s.t. <math>g_0^f(\cdot)</math> and <math>g_0^c(\cdot)</math> satisfy some sparsity and continuity constraints. | ||
The goal of the counterfactual generator is to fool the discriminator. Therefore, its optimal strategy is to match the counterfactual rationale distribution with the factual | |||
rationale distribution. The goal of the factual generator is to help the discriminator. Therefore, its optimal strategy, given the optimized counterfactual generator, is to | |||
“steer” the factual rationale distribution away from the counterfactual rationale distribution. | |||
Revision as of 11:40, 25 November 2021
Presented by
Yushan Chen, Yuying Huang, Ankitha Anugu
Introduction
The selection of input features can be optimised for trained models or can be directly incorporated into methods. But an overall selection does not properly capture the useful rationales. So, a new game theoretic approach to class-dependent rationalization is introduced where the method is specifically trained to highlight evidence supporting alternative conclusions. Each class consists of three players who compete to find evidence for both factual and counterfactual circumstances. In a simple example, we explain how the game drives the solution towards relevant class-dependent rationales theoretically.
Previous Work
There are two directions of research on generating interpretable features of neural networks. The first is to include the interpretations directly in the models, often known as self-explaining models. The alternative option is to generate interpretations in post-hoc manner. There are also few research works attempting to increase the fidelity of post hoc explanations by including the explanation mechanism into the training approach. Although none of these works can perform class-wise rationalisation, gradient based methods can be intuitively modified for this purpose, generating explanations for a specific class by probing the importance with regard to the relevant class logit.
Motivation
Extending how rationales are defined and calculated is one of the primary questions motivating this research. To date, the typical approach has been to choose an overall feature subset that best explains the output/decision. The greatest mutual information criterion, for example, selects an overall subset of features so that mutual information between the feature subset and the target output decision is maximised, or the entropy of the target output decision conditional on this subset is minimised. Rationales, on the other hand, can be multi-faceted, involving support for a variety of outcomes in varying degrees. Existing rationale algorithms have one limitation. They only look for rationales that support the label class. So, we propose CAR algorithm to find rationales of any given class.
Model Architecture
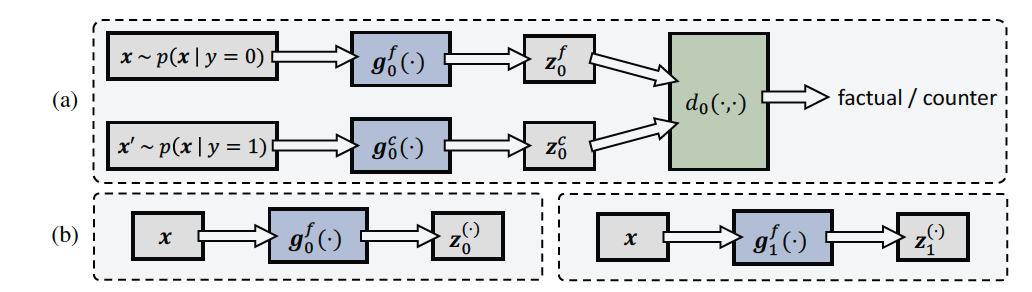
Suppose X is a random vector representing a string of text, Y represents the class that X is in, [math]\displaystyle{ Y\in \mathbb Y=\{0,1\} . }[/math] Z(t) provides evidence supporting class [math]\displaystyle{ t\in \{0,1\} . }[/math] [math]\displaystyle{ g_t^f(X), g_t^c(X), t\in \{0,1\} }[/math] are factual rationale generators, and [math]\displaystyle{ d_t(Z), t\in \{0,1\} }[/math] are discriminators.
Discriminator: In our adversarial game, [math]\displaystyle{ d_0(\cdot) }[/math] takes a rationale Z generated by either [math]\displaystyle{ g_0^f(\cdot) }[/math] or [math]\displaystyle{ g_0^c(\cdot) }[/math] as input, and outputs the probability that Z is generated by the factual generator [math]\displaystyle{ g_0^f(\cdot) }[/math]. The training target for [math]\displaystyle{ d_0(\cdot) }[/math] is similar to the generative adversarial network (GAN) [6]:
[math]\displaystyle{ d(\cdot)=\underset{d(\cdot)}{argmin} -p_Y(0)\mathrm{E}[\log d(g_0^f(X))|Y=0]-p_Y(1)\mathrm{E}[\log(1- d(g_0^c(X)))|Y=1] }[/math]
Generators: The factual generator [math]\displaystyle{ g_0^f(\cdot) }[/math] is trained to generate rationales from text labeled Y = 0. The counterfactual generator [math]\displaystyle{ g_0^c(\cdot) }[/math], in contrast, learns from text labeled Y = 1. Both generators try to convince the discriminator that they are factual generators for Y = 0.
[math]\displaystyle{ g_0^f(\cdot)=\underset{g(\cdot)}{argmax}\mathrm{E}[h_0(d_0(g(X)))|Y=0] }[/math], and [math]\displaystyle{ g_0^c(\cdot)=\underset{g(\cdot)}{argmax}\mathrm{E}[h_1(d_0(g(X)))|Y=1] }[/math],
s.t. [math]\displaystyle{ g_0^f(\cdot) }[/math] and [math]\displaystyle{ g_0^c(\cdot) }[/math] satisfy some sparsity and continuity constraints.
The goal of the counterfactual generator is to fool the discriminator. Therefore, its optimal strategy is to match the counterfactual rationale distribution with the factual rationale distribution. The goal of the factual generator is to help the discriminator. Therefore, its optimal strategy, given the optimized counterfactual generator, is to “steer” the factual rationale distribution away from the counterfactual rationale distribution.
Figure 1: CAR training and inference procedures of the class-0 case. (a) The training procedure. (b) During inference, there is no ground truth label. In this case, we will always trigger the factual generators.
Experiments
The authors evaluated factual and counterfactual rational generation in both single- and multi-aspect classification tasks. The method was tested on the following three binary classification datasets: Amazon reviews (single-aspect) [1], Beer reviews (multi-aspect) [2], and Hotel reviews (multi-aspect) [3]. Note that the Amazon reviews contain both positive and negative sentiments. Beer reviews and hotel reviews contain only factual annotations.
The CAR model is compared with two existing methods, RNP and Post-exp.
- RNP: this is a framework for rationalizing neural prediction proposed by Lei et al. [4]. It combines two modular components, a generator, and a predictor. RNP is only able to generate factual rationales.
- POST-EXP: Post-explanation approach contains two generators and one predictor. Given the pre-trained predictor, one generator is trained to generate positive rationales, and the other generator is trained to generate negative rationales.
To make reasonable comparisons among the three methods, the predictors are of the same architecture, so as the generators. Their sparsity and continuity constraints are also of the same form.
Two types are experiments are set: objective evaluation and subjective evaluation.
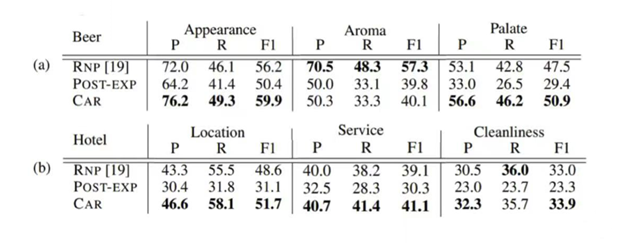
In the objective evaluation, rationales are generated using the three models, and are compared with human annotations. Precision, recall and F1 score are reported to evaluate the performance of the models. (Note that the algorithms are conditioned on a similar actual sparsity level in factual rationales.)
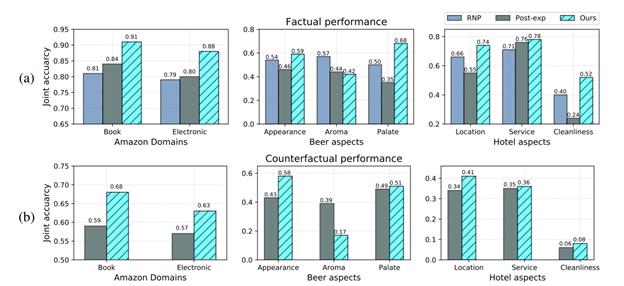
In the subjective evaluations, people were asked to choose a sentiment (positive or negative) based on the given rationales. In the single-aspect case, a success is credited when the person correctly guesses the ground-truth sentiment given the factual rationales, or the person is convinced to choose the opposite sentiment to the ground-truth given the counterfactual rationale. In the multi-aspect case, the person also needs to guess the aspect correctly.
The results are as below.
Table 1: Objective performances on the Amazon review dataset. The numbers in each column represent precision / recall / F1 score. [5]
Table 2: Objective performances on the beer review and hotel review datasets. (Columns: P - precision / R - recall / F1 - F1 score.) [5]
Figure 3: Subjective performances summary. [5]
Conclusions
The authors evaluated the method in single- and multi-aspect sentiment classification tasks. The result tables above show that the proposed method is able to identify both factual (justifying the ground truth label) and counterfactual (countering the ground truth label) rationales consistent with human rationalization. When comparing with other existing methods (RNP and POST-EXP), CAR achieves better accuracy in finding factual rationales. For the counterfactual case, although the CAR method has lower recall and F1 score, human evaluators still favor the CAR generated counterfactual rationales. The subjective experiment result shows that CAR is able to correctly convince the subjects with factual rationales and fool the subjects with counterfactual rationales.
Critiques
Although the CAR method performs better than the two other methods in most cases, it still has many limitations. In the case where the reviews have annotated ground truth containing mixed sentiments (aroma aspect in beer reviews), CAR often has low recalls. Also, CAR sometimes selects irrelevant aspect words with the desired sentiment to fulfill the sparsity constraint. This reduces the precision. When the reviews are very short without a mix of sentiments (cleanliness aspect in hotel reviews), it is hard for CAR to generate counterfactual rationales to trick a human.
-
References
[1] John Blitzer, Mark Dredze, and Fernando Pereira. Biographies, bollywood, boom-boxes and blenders: Domain adaptation for sentiment classification. In Proceedings of the 45th annual meeting of the association of computational linguistics, pages 440–447, 2007.
[2] Julian McAuley, Jure Leskovec, and Dan Jurafsky. Learning attitudes and attributes from multi-aspect reviews. In 2012 IEEE 12th International Conference on Data Mining, pages 1020–1025. IEEE, 2012.
[3] Hongning Wang, Yue Lu, and Chengxiang Zhai. Latent aspect rating analysis on review text data: a rating regression approach. In Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining, pages 783–792. ACm, 2010.
[4] Tao Lei, Regina Barzilay, and Tommi Jaakkola. Rationalizing neural predictions. arXiv preprint arXiv:1606.04155, 2016
[5] Shiyu Chang, Yang Zhang, Mo Yu, and Tommi Jaakkola. A game theoretic approach to class-wise selective rationalization. arXiv: 1910.12853, 2019
[6] Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y. Generative adversarial nets. Advances in neural information processing systems. 2014;27.