"Why Should I Trust You?": Explaining the Predictions of Any Classifier: Difference between revisions
No edit summary |
No edit summary |
||
| Line 35: | Line 35: | ||
In addition to explaining predictions, providing a global perspective is important to ascertain trust in the model. As mentioned before, accuracy may often not be a suitable metric to evaluate the model, and thus we want to explain the model. Building upon the explanations for individual predictions, we select a few explanations to present to the user, such that they are representative of the model. | In addition to explaining predictions, providing a global perspective is important to ascertain trust in the model. As mentioned before, accuracy may often not be a suitable metric to evaluate the model, and thus we want to explain the model. Building upon the explanations for individual predictions, we select a few explanations to present to the user, such that they are representative of the model. | ||
==Local Interpretable Model-Agnostic Explanations (LIME)== | |||
The overall goal of LIME is to identify an interpretable model over the interpretable representation that is locally faithful to the classifier. A possible interpretable representation for text classification is a binary vector indicating the presence or absence of a word, even though the classifier may use more complex (and incomprehensible) features such as word embeddings. Likewise for image classification, an interpretable representation may be a binary vector indicating the “presence” or “absence” of a contiguous patch of similar pixels (a super-pixel), while the classifier may represent the image as a tensor with three color channels per pixel. We denote x ∈ R d be the original representation of an instance being explained, and we use x 0 ∈ {0, 1} d 0 to denote a binary vector for its interpretable representation. | |||
Formally, we define an explanation as a model g ∈ G, where G is a class of potentially interpretable models, such as linear models, decision trees, or falling rule lists [27], i.e. a model g ∈ G can be readily presented to the user with visual or textual artifacts. The domain of g is {0, 1} d 0 , i.e. g acts over absence/presence of the interpretable components. As not every g ∈ G may be simple enough to be interpretable - thus we let Ω(g) be a measure of complexity (as opposed to interpretability) of the explanation g ∈ G. For example, for decision trees Ω(g) may be the depth of the tree, while for linear models, Ω(g) may be the number of non-zero weights. Let the model being explained be denoted f : R d → R. In classification, f(x) is the probability (or a binary indicator) that x belongs to a certain class1 . We further use πx(z) as a proximity measure between an instance z to x, so as to define locality around x. Finally, let L(f, g, πx) be a measure of how unfaithful g is in approximating f in the locality defined by πx. In order to ensure both interpretability and local fidelity, we must minimize L(f, g, πx) while having Ω(g) be low enough to be interpretable by humans. The explanation produced by LIME is obtained by the following: | |||
:<math>\xi(x) = \underset{g\in\mathbb{G}}{\operatorname{arg\,min}}\, \mathcal{L}(f,g,\pi) + \Omega(g)</math> | |||
This formulation can be used with different explanation families G, fidelity functions L, and complexity measures Ω. Here we focus on sparse linear models as explanations, and on performing the search using perturbations. | |||
== Sampling for Local Exploration == | |||
We want to minimize the locality-aware loss L(f, g, πx) without making any assumptions about f, since we want the explainer to be model-agnostic. Thus, in order to learn the local behavior of f as the interpretable inputs vary, we approximate L(f, g, πx) by drawing samples, weighted by πx. We sample instances around x 0 by drawing nonzero elements of x 0 uniformly at random (where the number of such draws is also uniformly sampled). Given a perturbed sample z 0 ∈ {0, 1} d 0 (which contains a fraction of the nonzero elements of x 0 ), we recover the sample in the original representation z ∈ R d and obtain f(z), which is used as a label for the explanation model. Given this dataset Z of perturbed samples with the associated labels, we optimize Eq. (1) to get an explanation ξ(x). The primary intuition behind LIME is presented in Figure 3, where we sample instances both in the vicinity of x (which have a high weight due to πx) and far away from x (low weight from πx). Even though the original model may be too complex to explain globally, LIME presents an explanation that is locally faithful (linear in this case), where the locality is captured by πx. It is worth noting that our method is fairly robust to sampling noise since the samples are weighted by πx in Eq. (1). We now present a concrete instance of this general framework. | |||
==Sparse Linear Explanations== | |||
For the rest of this paper, we let G be the class of linear models, such that g(z 0 ) = wg ·z 0 . We use the locally weighted square loss as L, as defined in Eq. (2), where we let πx(z) = exp(−D(x, z) 2 /σ2 ) be an exponential kernel defined on some distance function D (e.g. cosine distance for text, L2 distance for images) with width σ. | |||
space for equation - L2 loss minimization | |||
For text classification, we ensure that the explanation is interpretable by letting the interpretable representation be a bag of words, and by setting a limit K on the number of words, i.e. Ω(g) = ∞1[kwgk0 > K]. Potentially, K can be adapted to be as big as the user can handle, or we could have different values of K for different instances. In this paper we use a constant value for K, leaving the exploration of different values to future work. We use the same Ω for image classification, using “super-pixels” (computed using any standard algorithm) instead of words, such that the interpretable representation of an image is a binary vector where 1 indicates the original super-pixel and 0 indicates a grayed out super-pixel. This particular choice of Ω makes directly solving Eq. (1) intractable, but we approximate it by first selecting K features with Lasso (using the regularization path [9]) and then learning the weights via least squares (a procedure we call K-LASSO in Algorithm 1). Since Algorithm 1 produces an explanation for an individual prediction, its complexity does not depend on the size of the dataset, but instead on time to compute f(x) and on the number of samples N. In practice, explaining random forests with 1000 trees using scikit-learn (http://scikit-learn.org) on a laptop with N = 5000 takes under 3 seconds without any optimizations such as using gpus or parallelization. Explaining each prediction of the Inception network [25] for image classification takes around 10 minutes. | |||
Any choice of interpretable representations and G will have some inherent drawbacks. First, while the underlying model can be treated as a black-box, certain interpretable representations will not be powerful enough to explain certain behaviors. For example, a model that predicts sepia-toned images to be retro cannot be explained by presence of absence of super pixels. Second, our choice of G (sparse linear models) means that if the underlying model is highly non-linear even in the locality of the prediction, there may not be a faithful explanation. However, we can estimate the faithfulness of Algorithm 1 Sparse Linear Explanations using LIME Require: Classifier f, Number of samples N Require: Instance x, and its interpretable version x 0 Require: Similarity kernel πx, Length of explanation K Z ← {} for i ∈ {1, 2, 3, ..., N} do z 0 i ← sample around(x 0 ) Z ← Z ∪ hz 0 i , f(zi), πx(zi)i end for w ← K-Lasso(Z, K) . with z 0 i as features, f(z) as target return w the explanation on Z, and present this information to the user. This estimate of faithfulness can also be used for selecting an appropriate family of explanations from a set of multiple interpretable model classes, thus adapting to the given dataset and the classifier. We leave such exploration for future work, as linear explanations work quite well for multiple black-box models in our experiments. | |||
Revision as of 04:59, 12 November 2017
Introduction
Understanding why machine learning models behave the way they do empowers both system designers and end-users in many ways: in model selection, feature engineering, in order to trust and act upon the predictions, and in more intuitive user interfaces. Thus, interpretability has become a vital concern in machine learning, and work in the area of interpretable models has found renewed interest. In some applications, such models are as accurate as non-interpretable ones, and thus are preferred for their transparency. Even when they are not accurate, they may still be preferred when interpretability is of paramount importance. However, restricting machine learning to interpretable models is often a severe limitation. In this paper the authors argue for explaining machine learning predictions using model-agnostic approaches and propose LIME, a novel explanation technique that explains the predictions of any classifier in an interpretable and faithful manner, by learning an interpretable model locally around the prediction. They also propose a method to explain models by presenting representative individual predictions and their explanations in a non-redundant way, framing the task as a submodular optimization problem.
The authors demonstrate the flexibility of these methods by explaining different models for text (e.g. random forests) and image classification (e.g. convolutional neural networks). They show the utility of explanations via novel experiments, both simulated and with human subjects, on various scenarios that require trust: deciding if one should trust a prediction, choosing between models, improving an untrustworthy classifier, and identifying why a classifier should not be trusted.
In this paper, we propose providing explanations for individual predictions as a solution to the “trusting a prediction” problem, and selecting multiple such predictions (and explanations) as a solution to the “trusting the model” problem. Our main contributions are summarized as follows.
- . LIME, an algorithm that can explain the predictions of any classifier or regressor in a faithful way, by approximating it locally with an interpretable model.
- . SP-LIME, a method that selects a set of representative instances with explanations to address the “trusting the model” problem, via submodular optimization.
- Comprehensive evaluation with simulated and human subjects, where we measure the impact of explanations on trust and associated tasks. In our experiments, non-experts using LIME are able to pick which classifier from a pair generalizes better in the real world. Further, they are able to greatly improve an untrustworthy classifier trained on 20 newsgroups, by doing feature engineering using LIME. We also show how understanding the predictions of a neural network on images helps practitioners know when and why they should not trust a model.
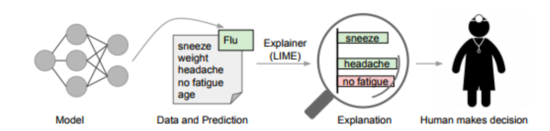
The Case for Explanations
By “explaining a prediction”, we mean presenting textual or visual artifacts that provide qualitative understanding of the relationship between the instance’s components (e.g. words in text, patches in an image) and the model’s prediction. We argue that explaining predictions is an important aspect in getting humans to trust and use machine learning effectively, if the explanations are faithful and intelligible. The process of explaining individual predictions is illustrated in Figure 1. It is clear that a doctor is much better positioned to make a decision with the help of a model if intelligible explanations are provided. In this case, an explanation is a small list of symptoms with relative weights – symptoms that either contribute to the prediction (in green) or are evidence against it (in red). Humans usually have prior knowledge about the application domain, which they can use to accept (trust) or reject a prediction if they understand the reasoning behind it. It has been observed, for example, that providing explanations can increase the acceptance of movie recommendations [12] and other automated systems [8].
There are several ways a model or its evaluation can go wrong. Data leakage, for example, defined as the unintentional leakage of signal into the training (and validation) data that would not appear when deployed [14], potentially increases accuracy. A challenging example cited by Kaufman et al. [14] is one where the patient ID was found to be heavily correlated with the target class in the training and validation data. This issue would be incredibly challenging to identify just by observing the predictions and the raw data, but much easier if explanations such as the one in Figure 1 are provided, as patient ID would be listed as an explanation for predictions. Another particularly hard to detect problem is dataset shift [5], where training data is different than test data (we give an example in the famous 20 newsgroups dataset later on). The insights given by explanations are particularly helpful in identifying what must be done to convert an untrustworthy model into a trustworthy one – for example, removing leaked data or changing the training data to avoid dataset shift.
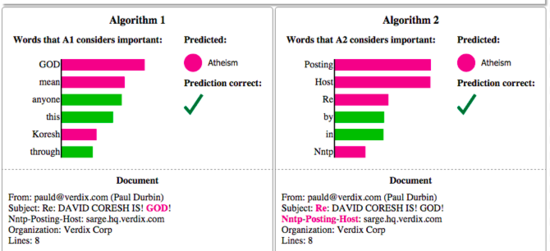
Machine learning practitioners often have to select a model from a number of alternatives, requiring them to assess the relative trust between two or more models. In Figure Figure 2: Explaining individual predictions of competing classifiers trying to determine if a document is about “Christianity” or “Atheism”. The bar chart represents the importance given to the most relevant words, also highlighted in the text. Color indicates which class the word contributes to (green for “Christianity”, magenta for “Atheism”). 2, we show how individual prediction explanations can be used to select between models, in conjunction with accuracy. In this case, the algorithm with higher accuracy on the validation set is actually much worse, a fact that is easy to see when explanations are provided (again, due to human prior knowledge), but hard otherwise. Further, there is frequently a mismatch between the metrics that we can compute and optimize (e.g. accuracy) and the actual metrics of interest such as user engagement and retention. While we may not be able to measure such metrics, we have knowledge about how certain model behaviors can influence them. Therefore, a practitioner may wish to choose a less accurate model for content recommendation that does not place high importance in features related to “clickbait” articles (which may hurt user retention), even if exploiting such features increases the accuracy of the model in cross validation. We note that explanations are particularly useful in these (and other) scenarios if a method can produce them for any model, so that a variety of models can be compared.
Desired Characteristics for Explainers
An essential criterion for explanations is that they must be interpretable, i.e., provide qualitative understanding between the input variables and the response. We note that interpretability must take into account the user’s limitations. Thus, a linear model [24], a gradient vector [2] or an additive model [6] may or may not be interpretable. For example, if hundreds or thousands of features significantly contribute to a prediction, it is not reasonable to expect any user to comprehend why the prediction was made, even if individual weights can be inspected. This requirement further implies that explanations should be easy to understand, which is not necessarily true of the features used by the model, and thus the “input variables” in the explanations may need to be different than the features. Finally, we note that the notion of interpretability also depends on the target audience. Machine learning practitioners may be able to interpret small Bayesian networks, but laymen may be more comfortable with a small number of weighted features as an explanation.
Another essential criterion is local fidelity. Although it is often impossible for an explanation to be completely faithful unless it is the complete description of the model itself, for an explanation to be meaningful it must at least be locally faithful, i.e. it must correspond to how the model behaves in the vicinity of the instance being predicted. We note that local fidelity does not imply global fidelity: features that are globally important may not be important in the local context, and vice versa. While global fidelity would imply local fidelity, identifying globally faithful explanations that are interpretable remains a challenge for complex models. While there are models that are inherently interpretable [6, 17, 26, 27], an explainer should be able to explain any model, and thus be model-agnostic (i.e. treat the original model as a black box). Apart from the fact that many state-ofthe-art classifiers are not currently interpretable, this also provides flexibility to explain future classifiers.
In addition to explaining predictions, providing a global perspective is important to ascertain trust in the model. As mentioned before, accuracy may often not be a suitable metric to evaluate the model, and thus we want to explain the model. Building upon the explanations for individual predictions, we select a few explanations to present to the user, such that they are representative of the model.
Local Interpretable Model-Agnostic Explanations (LIME)
The overall goal of LIME is to identify an interpretable model over the interpretable representation that is locally faithful to the classifier. A possible interpretable representation for text classification is a binary vector indicating the presence or absence of a word, even though the classifier may use more complex (and incomprehensible) features such as word embeddings. Likewise for image classification, an interpretable representation may be a binary vector indicating the “presence” or “absence” of a contiguous patch of similar pixels (a super-pixel), while the classifier may represent the image as a tensor with three color channels per pixel. We denote x ∈ R d be the original representation of an instance being explained, and we use x 0 ∈ {0, 1} d 0 to denote a binary vector for its interpretable representation.
Formally, we define an explanation as a model g ∈ G, where G is a class of potentially interpretable models, such as linear models, decision trees, or falling rule lists [27], i.e. a model g ∈ G can be readily presented to the user with visual or textual artifacts. The domain of g is {0, 1} d 0 , i.e. g acts over absence/presence of the interpretable components. As not every g ∈ G may be simple enough to be interpretable - thus we let Ω(g) be a measure of complexity (as opposed to interpretability) of the explanation g ∈ G. For example, for decision trees Ω(g) may be the depth of the tree, while for linear models, Ω(g) may be the number of non-zero weights. Let the model being explained be denoted f : R d → R. In classification, f(x) is the probability (or a binary indicator) that x belongs to a certain class1 . We further use πx(z) as a proximity measure between an instance z to x, so as to define locality around x. Finally, let L(f, g, πx) be a measure of how unfaithful g is in approximating f in the locality defined by πx. In order to ensure both interpretability and local fidelity, we must minimize L(f, g, πx) while having Ω(g) be low enough to be interpretable by humans. The explanation produced by LIME is obtained by the following:
- [math]\displaystyle{ \xi(x) = \underset{g\in\mathbb{G}}{\operatorname{arg\,min}}\, \mathcal{L}(f,g,\pi) + \Omega(g) }[/math]
This formulation can be used with different explanation families G, fidelity functions L, and complexity measures Ω. Here we focus on sparse linear models as explanations, and on performing the search using perturbations.
Sampling for Local Exploration
We want to minimize the locality-aware loss L(f, g, πx) without making any assumptions about f, since we want the explainer to be model-agnostic. Thus, in order to learn the local behavior of f as the interpretable inputs vary, we approximate L(f, g, πx) by drawing samples, weighted by πx. We sample instances around x 0 by drawing nonzero elements of x 0 uniformly at random (where the number of such draws is also uniformly sampled). Given a perturbed sample z 0 ∈ {0, 1} d 0 (which contains a fraction of the nonzero elements of x 0 ), we recover the sample in the original representation z ∈ R d and obtain f(z), which is used as a label for the explanation model. Given this dataset Z of perturbed samples with the associated labels, we optimize Eq. (1) to get an explanation ξ(x). The primary intuition behind LIME is presented in Figure 3, where we sample instances both in the vicinity of x (which have a high weight due to πx) and far away from x (low weight from πx). Even though the original model may be too complex to explain globally, LIME presents an explanation that is locally faithful (linear in this case), where the locality is captured by πx. It is worth noting that our method is fairly robust to sampling noise since the samples are weighted by πx in Eq. (1). We now present a concrete instance of this general framework.
Sparse Linear Explanations
For the rest of this paper, we let G be the class of linear models, such that g(z 0 ) = wg ·z 0 . We use the locally weighted square loss as L, as defined in Eq. (2), where we let πx(z) = exp(−D(x, z) 2 /σ2 ) be an exponential kernel defined on some distance function D (e.g. cosine distance for text, L2 distance for images) with width σ.
space for equation - L2 loss minimization
For text classification, we ensure that the explanation is interpretable by letting the interpretable representation be a bag of words, and by setting a limit K on the number of words, i.e. Ω(g) = ∞1[kwgk0 > K]. Potentially, K can be adapted to be as big as the user can handle, or we could have different values of K for different instances. In this paper we use a constant value for K, leaving the exploration of different values to future work. We use the same Ω for image classification, using “super-pixels” (computed using any standard algorithm) instead of words, such that the interpretable representation of an image is a binary vector where 1 indicates the original super-pixel and 0 indicates a grayed out super-pixel. This particular choice of Ω makes directly solving Eq. (1) intractable, but we approximate it by first selecting K features with Lasso (using the regularization path [9]) and then learning the weights via least squares (a procedure we call K-LASSO in Algorithm 1). Since Algorithm 1 produces an explanation for an individual prediction, its complexity does not depend on the size of the dataset, but instead on time to compute f(x) and on the number of samples N. In practice, explaining random forests with 1000 trees using scikit-learn (http://scikit-learn.org) on a laptop with N = 5000 takes under 3 seconds without any optimizations such as using gpus or parallelization. Explaining each prediction of the Inception network [25] for image classification takes around 10 minutes.
Any choice of interpretable representations and G will have some inherent drawbacks. First, while the underlying model can be treated as a black-box, certain interpretable representations will not be powerful enough to explain certain behaviors. For example, a model that predicts sepia-toned images to be retro cannot be explained by presence of absence of super pixels. Second, our choice of G (sparse linear models) means that if the underlying model is highly non-linear even in the locality of the prediction, there may not be a faithful explanation. However, we can estimate the faithfulness of Algorithm 1 Sparse Linear Explanations using LIME Require: Classifier f, Number of samples N Require: Instance x, and its interpretable version x 0 Require: Similarity kernel πx, Length of explanation K Z ← {} for i ∈ {1, 2, 3, ..., N} do z 0 i ← sample around(x 0 ) Z ← Z ∪ hz 0 i , f(zi), πx(zi)i end for w ← K-Lasso(Z, K) . with z 0 i as features, f(z) as target return w the explanation on Z, and present this information to the user. This estimate of faithfulness can also be used for selecting an appropriate family of explanations from a set of multiple interpretable model classes, thus adapting to the given dataset and the classifier. We leave such exploration for future work, as linear explanations work quite well for multiple black-box models in our experiments.