discLDA: Discriminative Learning for Dimensionality Reduction and Classification

Introduction

Dimensionality reduction is a common and often necessary step in most machine learning applications and high-dimensional data analyses. There exists some linear methods for dimensionality reduction such as principal component analysis (PCA) and Fisher discriminant analysis (FDA) and some nonlinear procedures such as kernelized versions of PCA and FDA as well as manifold learning algorithms.

A recent trend in dimensionality reduction is to focus on probabilistic models. These models, which include generative topological mapping, factor analysis, independent component analysis and probabilistic latent semantic analysis (pLSA), are generally specified in terms of an underlying independence assumption or low-rank assumption. The models are generally fit with maximum likelihood, although Bayesian methods are sometimes used. Such Bayesian methods are based on the well-known Bayes' Theorem from probability theory which is often very useful for classification tasks; for instance, it is used as the foundation of the theoretically-optimal Bayes classifier.

Although the mentioned dimensionality reduction techniques are unsupervised, another trend of research is being conducted on the supervised techniques. These techniques, such as sufficient dimensionality reduction (SDR) utilizes labeled data. A supervised dimensionality reduction technique can also be applied to build a classifier or regressor on the reduced space.

The goal of this paper is basically to introduce a supervised version of LDA. Not only the unsupervised dimensionality reduction features of LDA are preserved and used, but also the side information of class labels are incorporated.

LDA

Latent Dirichlet Allocation (LDA) is a Bayesian model in the spirit of probabilistic latent semantic analysis (pLSA) that models each data point (e.g., a document) as a collection of draws from a mixture model in which each mixture component is known as a topic.

The history of LDA can be traced to Johann Dirichlet(1805 - 1859) , who was a well-known German mathematical whose many well-known works and contributions include the Pigeonhole principle and the Dirichlet distribution. According to Oxford Advanced Learner’s Dictionary, the word latent means existing but not yet active, developed or visible and the term allocate means to distribute sth officially to sb/sth for a special purpose. Thus, we can use this generative probabilistic model (LDA) when we apply statistics to working with and handling collections of discrete data. LDA is particularly useful when it is applied to text corpora data to enable us to more easily classify documents so as to speed up the way that Google searches for documents. This application is often termed document modeling, and its two main goals are to find short descriptions for the member of a collection and to preserve the essential statistic relationships between these members, both of which LDA has been found to be quite good at.

Before going on further, we shall have a brief overview on generative probabilistic models. A generative probabilistic model assumes that the observed data is generated by some parameterized random process (a random variable), uses the available training data to learn the values of the parameters of the underlying distribution that best explain the observed data, and then uses the constructed model to predict new data. Generative probabilistic models have many advantages over non-generative models. Two such advantages are 1. the assumptions and the model are explicit and 2. well-known algorithms such as EM and Markov Chain Monte Carlo can be used for both training the model and for predicting new data.

As mentioned above, LDA can be considered to be a modified form of probabilistic latent semantic indexing (pLSI). pLSI models each word in a document as a sample from a mixture model, and it also introduces the concept of a topic and assumes that each word is generated by one topic and different words can be generated by different topics. However, pLSI faces many shortcomings, two of which are that it is not well-defined on the level of documents and that it is prone to over-fitting due to having many parameters that number to kV + kM, where V is the number of words in the vocabulary, M is the number of documents, and k is the number of mixtures. pLSI assumes that the order of words in a document is not important and can therefore be neglected when training the model. This is the bag-of-words assumption mentioned above. We shall now look at a couple of definitions. A finite set of random variables is said to be exchangeable if their joint probability distribution is invariant under permutation, and an infinite sequence of random variables is said to be infinitely exchangeable if every finite sequence of these random variables is exchangeable. The two main assumptions that underlie LDA are:

• The words are generated by topics by means of a fixed conditional distribution.
• The topics in a document are themselves infinitely exchangeable.

With the two above assumptions in mind, and using de Finetti's Theorem whose statement and usage are described in the link 2 given in the References, the probability of a sequence of words and topics under LDA has the form [math]\displaystyle{ \, p(w , z) = \int p(\theta) ( \prod_{n=1}^N p(z_n | \theta) p(w_n | z_n)) d \theta }[/math], where [math]\displaystyle{ \theta }[/math] is the random parameter of a multinomial distribution over the topics. One more piece of information, the correct distribution of [math]\displaystyle{ \, p(\theta) }[/math], remains to be determined. Unfortunately, because de Finetti's Theorem is not constructive, an assumption must be made regarding the distribution of [math]\displaystyle{ \, p(\theta) }[/math]. Blei et al. in their 2003 paper made the assumption that the distribution of [math]\displaystyle{ \, p(\theta) }[/math] is the Dirichlet distribution, and this is where the name Latent Dirichlet Allocation (LDA) comes from. There was a good reason why Blei et al. assumed the Dirichlet distribution for [math]\displaystyle{ \, p(\theta) }[/math]. Relating to the Bayes' formula mentioned above, the Dirichlet distribution is conjugate to the multinomial distribution; and since we would like to use LDA to solve an inference problem when new data points become available, we would like to make the prior as simple as possible. With the assumptions underlying LDA and the Dirichlet distribution as foundation, the LDA algorithm is simple and can be described with a few steps. For the interested reader, a pictorial description of the steps of LDA are available on pages 21 and 22 of the link 2 in the References. Last but not the least, when a new data point, i.e. a new document, becomes available, how can we determine to which topics does it belong to? This is the problem of inference which we would like to ultimately solve when we are using LDA to work with text corpus data. For the interested reader, the inference problem of LDA as well as LDA's closely-related problem of the estimation and the smoothing of the parameters [math]\displaystyle{ \, \beta }[/math] are given on pages 27 to 29 of the link 2 in the References.

LDA is a three-level hierarchical Bayesian model, in which each item of a collection is modeled as a finite mixture over an underlying set of topics. Each topic is, in turn, modeled as an infinite mixture over an underlying set of topic probabilities. In the context of text modeling, the topic probabilities provide an explicit representation of a document.

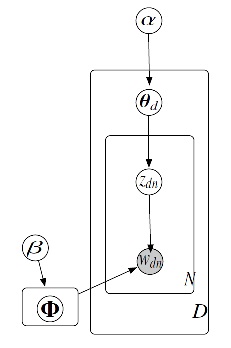
Taken from [1], Fig. 1 shows the generative process for the vector w_d which is a bag-of-words representation of document d. It contains three steps which are as follows:

1) [math]\displaystyle{ \theta_d }[/math] ~ Dir [math]\displaystyle{ (\alpha) }[/math]

2) z_dn ~ Multi [math]\displaystyle{ (\theta_d) }[/math]

3) w_dn ~ Multi [math]\displaystyle{ (\phi_{z_{dn}}) }[/math]

Given a set of documents, {w_d}^D_d=1, the principle task is to estimate parameter {[math]\displaystyle{ \Phi_k }[/math]}^K_k=1. This is done by maximum likelihood, [math]\displaystyle{ \Phi }[/math]^* = argmax _{[math]\displaystyle{ \phi }[/math]} p ({w_d};[math]\displaystyle{ \Phi }[/math])

Fig.1 LDA model

DiscLDA

This paper presents a discriminative variation on Latent Dirichlet Allocation (LDA) in which a class-dependent linear transformation is introduced on the topic mixture proportions. This parameter is estimated by maximizing the conditional likelihood. By using the transformed topic mixture proportions as a new representation of documents, a supervised dimensionality reduction algorithm is obtained which uncovers the latent structure in a document collection while preserving predictive power for the task of classification. DiscLDA is supervised form of LDA. In DiscLDA, it is assumed that supervised side information is present, and that side information is taken into account in finding a reduced dimensionality representation. In particular, side information such as class labels are incorporated into LDA, while retaining its favorable unsupervised dimensionality reduction abilities. The goal is to develop parameter estimation procedures that yield LDA topics that characterize the corpus and maximally exploit the predictive power of the side information.

In DiscLDA method, each document is additionally associated with a categorial variable or class label y_d member of {1,2,...,C}, therefore for each class label y a linear transformaton T^y : R^K -> R^L₊ is introduced; which transforms a K-dimensional Dirichlet variable [math]\displaystyle{ \theta_d }[/math] to a mixture of Dirichlet distributions: T^y[math]\displaystyle{ \theta_d }[/math] [math]\displaystyle{ \isin }[/math] R^L. In order to generate a word w_dn, its topic z_dn is drawn from T^yd [math]\displaystyle{ \theta_d }[/math].

The following shows the steps in DiscLDA.

Fig.2 DiscLDA model

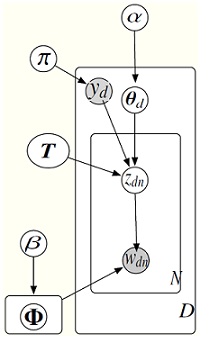
In DiscLDA there are class-dependent topic parameters [math]\displaystyle{ \phi }[/math]_k^y which determine the conditional distribution of the words:

[math]\displaystyle{ w_{dn} | z_{dn},y_d, \Phi }[/math] ~ [math]\displaystyle{ Multi }[/math] ([math]\displaystyle{ \phi }[/math] ^y_d _{z_{dn}} )

by marginalizing out the hidden topic vector z, we get the following distribution for the word w_dn given [math]\displaystyle{ \theta }[/math].

[math]\displaystyle{ w_{dn} | y_d, \theta_d, T }[/math] ~ [math]\displaystyle{ Multi }[/math] ([math]\displaystyle{ \Phi }[/math] [math]\displaystyle{ T }[/math]^y [math]\displaystyle{ \theta }[/math]_d )

Taken from [1], the illustration in Fig. 2 shows DiscLDA.

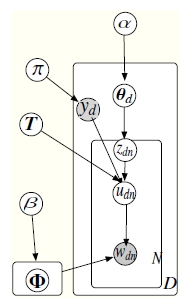
Furthermore, the parameterization of DiscLDA can be augmented by introducing auxiliary parameters whose values depend on the known class labels. These parameters can then be tuned by the discriminative criterion. Together with the original parameters of DiscLDA, these auxiliary parameters enable us to have not only the advantages of the likelihood-based training procedure but also enable us to have additional freedom for tracking the side information. Taken from [1], an illustration of DiscLDA augmented with auxiliary parameter [math]\displaystyle{ \, u }[/math] is shown in Fig. 3.

Fig.3 DiscLDA model having auxiliary parameter [math]\displaystyle{ \,u }[/math]

Inference and Learning

Parameter Estimation

If we are given a corpus of document and their lables, then we estimate the parameter T^y by maximizing the conditional likelihood [math]\displaystyle{ \Sigma_d }[/math] log p([math]\displaystyle{ y_d }[/math] [math]\displaystyle{ | }[/math][math]\displaystyle{ w_d }[/math] ; {T^y}, [math]\displaystyle{ \Phi }[/math]) while [math]\displaystyle{ \Phi }[/math] is held fixed.

For maximizeing the conditional likelihood objective with respect to T we use gradient ascent, for a fixed [math]\displaystyle{ \Phi }[/math].

The gradient can be estimated by Monte Carlo EM, with samples from the Gibsbs sampler. Threfore the gradient can be written as:

[math]\displaystyle{ \frac{\part}{\part T} }[/math] log p(y | w,T, [math]\displaystyle{ \Phi }[/math]) = E_qt^y(z) [[math]\displaystyle{ \frac{\part}{\part T} }[/math] log p (w,z | y,T, [math]\displaystyle{ \Phi }[/math]) ] - E_r_t(z)[[math]\displaystyle{ \frac{\part}{\part T} }[/math] log p (w,z | T, [math]\displaystyle{ \Phi }[/math])]

Also, in order to estimate the parameter [math]\displaystyle{ \Phi }[/math], we hold the transformation matrices fixed and the maximize the posterior of the model.

Dimensionality Reduction

In order to obtain a supervised dimensionality reduction method we use the average transformed topic vector as the reduced representation of a test document. We estimate it using

E[T^y [math]\displaystyle{ \theta }[/math] [math]\displaystyle{ | }[/math] [math]\displaystyle{ \Phi }[/math], w, T] = [math]\displaystyle{ \Sigma_y }[/math] p(y | [math]\displaystyle{ \Phi }[/math], w, T) E[ T^y [math]\displaystyle{ \theta }[/math] | y, [math]\displaystyle{ \Phi }[/math], w, T] where [math]\displaystyle{ \Sigma_y }[/math] p(y | [math]\displaystyle{ \Phi }[/math], w, T) can be estimated using harmonic mean estimator and E[ T^y [math]\displaystyle{ \theta }[/math] | y, [math]\displaystyle{ \Phi }[/math], w, T] can be estimated from MCMC samples of z.

Comparison of LDA and DiscLDA

As mentioned in the previous sections, DiscLDA is a variation on LDA; in which the LDA parametrization is augmented to include a transformation matrix and in which this matrix is learned via a conditional likelihood criterion. This approach allows DiscLDA to:

· Retain the ability of the LDA approach to find useful low-dimensional representations of documents

· Make use of discriminative side information (labels) in forming these representations

Fig.3 t-SNE 2D embedding of the E[T^y [math]\displaystyle{ \theta }[/math] [math]\displaystyle{ | }[/math] [math]\displaystyle{ \Phi }[/math], w, T] representation of News-groups documents, after fitting to the DiscLDA model (T is fixed).

Fig.4 t-SNE 2D embedding of the E[[math]\displaystyle{ \theta }[/math] [math]\displaystyle{ | }[/math] [math]\displaystyle{ \Phi }[/math], w, T] representation of News-groups documents, after fitting to the standard unsupervised LDA model.

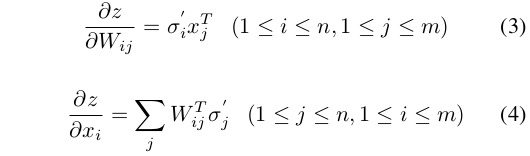
References

1. Simon Lacoste-Julien. Fei Sha. Michael I. Jordan. DiscLDA: Discriminative Learning for Dimensionality Reduction and Classification. [1]

2. Patrick Pletscher. Latent Dirichlet Allocation (LDA) written by Blei, Ng and Jordan slides, 13th December 2005. [2]