discLDA: Discriminative Learning for Dimensionality Reduction and Classification

Introduction

Dimensionality reduction is a common and often necessary step in most machine learning applications and high-dimensional data analyses. There exists some linear methods for dimensionality reduction such as principal component analysis (PCA) and Fisher discriminant analysis (FDA) and some nonlinear procedures such as kernelized versions of PCA and FDA as well as manifold learning algorithms.

A recent trend in dimensionality reduction is to focus on probabilistic models. These models, which include generative topological mapping, factor analysis, independent component analysis and probabilistic latent semantic analysis (pLSA), are generally specified in terms of an underlying independence assumption or low-rank assumption. The models are generally fit with maximum likelihood, although Bayesian methods are sometimes used.

LDA

Latent Dirichlet Allocation (LDA) is a Bayesian model in the spirit of probabilistic latent semantic analysis (pLSA) that models each data point (e.g., a document) as a collection of draws from a mixture model in which each mixture component is known as a topic.

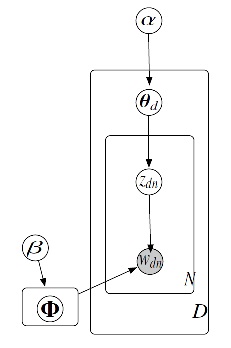
The figure 1 shows the generative process for the vector w_d which is a bag-of-word representation of document d. It contains three steps which are as follows:

1) [math]\displaystyle{ \theta_d }[/math] ~ Dir [math]\displaystyle{ (\alpha) }[/math]

2) z_dn ~ Multi [math]\displaystyle{ (\theta_d) }[/math]

3) w_dn ~ Multi [math]\displaystyle{ (\phi_{z_{dn}}) }[/math]

Given a set of documents, {w_d}^D_d=1, the principle task is to estimate parameter {[math]\displaystyle{ \Phi_k }[/math]}^K_k=1. This is done by maximum likelihood, [math]\displaystyle{ \Phi }[/math]^* = argmax _{[math]\displaystyle{ \phi }[/math]} p ({w_d};[math]\displaystyle{ \Phi }[/math])

Fig.1 LDA model

DiscLDA

This paper presents a discriminative variation on Latent Dirichlet Allocation (LDA) in which a class-dependent linear transformation is introduced on the topic mixture proportions. This parameter is estimated by maximizing the conditional likelihood. By using the transformed topic mixture proportions as a new representation of documents, a supervised dimensionality reduction algorithm is obtained which uncovers the latent structure in a document collection while preserving predictive power for the task of classification. DiscLDA is supervised form of LDA. In DiscLDA, it is assumed that supervised side information is present, and that side information is taken into account in finding a reduced dimensionality representation. In particular, side information such as class labels are incorporated into LDA, while retaining its favorable unsupervised dimensionality reduction abilities. The goal is to develop parameter estimation procedures that yield LDA topics that characterize the corpus and maximally exploit the predictive power of the side information.

In DiscLDA method, each document is additionally associated with a categorial variable or class label y_d member of {1,2,...,C}, therefore for each class label y a linear transformaton T^y : R^K -> R^L₊ is introduced; which transforms a K-dimensional Dirichlet variable [math]\displaystyle{ \theta_d }[/math] to a mixture of Dirichlet distributions: T^y[math]\displaystyle{ \theta_d }[/math] [math]\displaystyle{ \isin }[/math] R^L. In order to generate a word w_dn, its topic z_dn is drawn from T^yd [math]\displaystyle{ \theta_d }[/math].

The following figure shows the steps in DiscLDA.

Fig.2 DiscLDA model

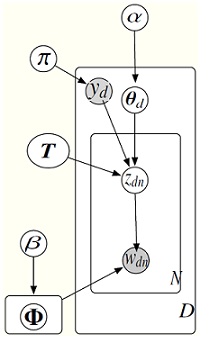
In DiscLDA there are class-dependant topic parameteres [math]\displaystyle{ \phi }[/math]_k^y which determine the conditional distribution of the words:

[math]\displaystyle{ w_{dn} | z_{dn},y_d, \Phi }[/math] ~ [math]\displaystyle{ Multi }[/math] ([math]\displaystyle{ \phi }[/math] ^y_d _{z_{dn}} )

by marginalizing out the hidden topic vector z, we get the following distribution for the word w_dn given [math]\displaystyle{ \theta }[/math].

[math]\displaystyle{ w_{dn} | y_d, \theta_d, T }[/math] ~ [math]\displaystyle{ Multi }[/math] ([math]\displaystyle{ \Phi }[/math] [math]\displaystyle{ T }[/math]^y [math]\displaystyle{ \theta }[/math]_d )

As mentioned above, DiscLDA is a variation on LDA; in which the LDA parametrization is augmented to include a transformation matrix and in which this matrix is learned via a conditional likelihood criterion. This approach allows DiscLDA to:

· Retain the ability of the LDA approach to find useful low-dimensional representations of documents

· Make use of discriminative side information (labels) in forming these representations