discLDA: Discriminative Learning for Dimensionality Reduction and Classification

Introduction

Dimensionality reduction is a common and often necessary step in most machine learning applications and high-dimensional data analyses. There exists some linear methods for dimensionality reduction such as principal component analysis (PCA) and Fisher discriminant analysis (FDA) and some nonlinear procedures such as kernelized versions of PCA and FDA as well as manifold learning algorithms.

A recent trend in dimensionality reduction is to focus on probabilistic models. These models, which include generative topological mapping, factor analysis, independent component analysis and probabilistic latent semantic analysis (pLSA), are generally specified in terms of an underlying independence assumption or low-rank assumption. The models are generally fit with maximum likelihood, although Bayesian methods are sometimes used.

LDA

Latent Dirichlet Allocation (LDA) is a Bayesian model in the spirit of probabilistic latent semantic analysis (pLSA) that models each data point (e.g., a document) as a collection of draws from a mixture model in which each mixture component is known as a topic.

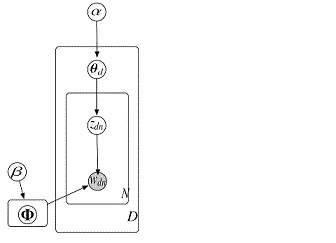
The figure 1 shows the generative process for the vector w_d which is a bag-of-word representation of document d. It contains three steps which are as follows:

1) [math]\displaystyle{ \theta_d }[/math] ~ Dir [math]\displaystyle{ (\alpha) }[/math]

2) z_dn ~ Multi [math]\displaystyle{ (\theta_d) }[/math]

3) w_dn ~ Multi [math]\displaystyle{ (\phi_{z_{dn}}) }[/math]

Given a set of documents, {w_d}^D_d=1, the principle task is to estimate parameter {[math]\displaystyle{ \Phi_k }[/math]}^K_k=1. This is done by maximum likelihood, [math]\displaystyle{ \Phi }[/math]^* = argmax _{[math]\displaystyle{ \phi }[/math]} p ({w_d};[math]\displaystyle{ \Phi }[/math])

Fig.2 A general construction for a single neuronLDA model