Point-of-Interest Recommendation: Exploiting Self-Attentive Autoencoders with Neighbor-Aware Influence

Presented by

Guanting(Tony) Pan, Zaiwei(Zara) Zhang, Haocheng(Beren) Chang

Introduction

With the development of mobile devices and location-acquisition technologies, accessing real-time location information is becoming easier and more efficient. Precisely because of this development, Location-based Social Networks (LBSNs) like Yelp and Foursquare have become an important part of human’s life. People can share their experiences in locations, such as restaurants and parks, on the Internet. These locations can be seen as a Point-of-Interest (POI) in software such as Maps on our phone. These large amounts of user-POI interaction data can provide a service, which is called personalized POI recommendation, to give recommendations to users that the location they might be interested in. These large amounts of data can be used to train a model through Machine Learning methods(i.e., Classification, Clustering, etc.) to predict a POI that users might be interested in. The POI recommendation system still faces some challenging issues: (1) the difficulty of modeling complex user-POI interactions from sparse implicit feedback; (2) the difficulty of incorporating geographic background information. In order to meet these challenges, this paper will introduce a novel autoencoder-based model to learn non-linear user-POI relations, which is called SAE-NAD. SAE stands for the self-attentive encoder, while NAD stands for the neighbor-aware decoder. Autoencoder is an unsupervised learning technique that we implement in the neural network model for representation learning, meaning that our neural network will contain a "bottleneck" layer that produces a compressed knowledge representation of the original input. This method will include machine learning knowledge that we learned in this course.

Previous Work

In the previous works, the method is just equally treating users checked in POIs. The drawback of equally treating users checked in POIs is that valuable information about the similarity between users is not utilized, thus reducing the power of such recommenders. However, the SAE adaptively differentiates the user preference degrees in multiple aspects.

There are some other personalized POI recommendation methods that can be used. Some famous software (e.g., Netflix) uses model-based methods that are built on matrix factorization (MF). For example, ranked based Geographical Factorization Method in [1] adopted weighted regularized MF to serve people on POI. Machine learning is popular in this area. POI recommendation is an important topic in the domain of recommender systems [4]. This paper also described related work in Personalized location recommendation and attention mechanism in the recommendation.

Motivation

This paper reviews encoder and decoder. A single hidden-layer autoencoder is an unsupervised neural network, which consists of two parts: an encoder and a decoder. The encoder has one activation function that maps the input data to the latent space. The decoder also has one activation function mapping the representations in the latent space to the reconstruction space. And here is the formula:

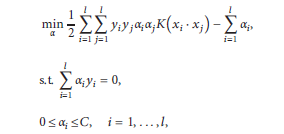
(Note: a is the activation function)

The proposed method uses a two-layer neural network to compute the score matrix in the architecture of the SAE. The NAD adopts the RBF kernel to make checked-in POIs exert more influence on nearby unvisited POIs. To train this model, Network training is required.

This paper will use the datasets in the real world, which are from Gowalla[2], Foursquare [3], and Yelp[3]. These datasets would be used to train by using the method introduced in this paper and compare the performance of SAE-NAD with other POI recommendation methods. Three groups of methods are used to compare with the proposed method, which are traditional MF methods for implicit feedback, Classical POI recommendation methods, and Deep learning-based methods. Specifically, the Deep learning-based methods contain a DeepAE which is a three-hidden-layer autoencoder with a weighted loss function, we can connect this to the material in this course.

Autoencoder (AE) due to their ability to represent complex data have become very useful in recommendation systems. The primary reason it is used is because with deep neural network and with non-linear activation function it effectively captures the non-linear and non-trivial relationships between users and POI's.

Methodology

Notations

Here are the notations used in this paper. It will be helpful when trying to understand the structure and equations in the algorithm.

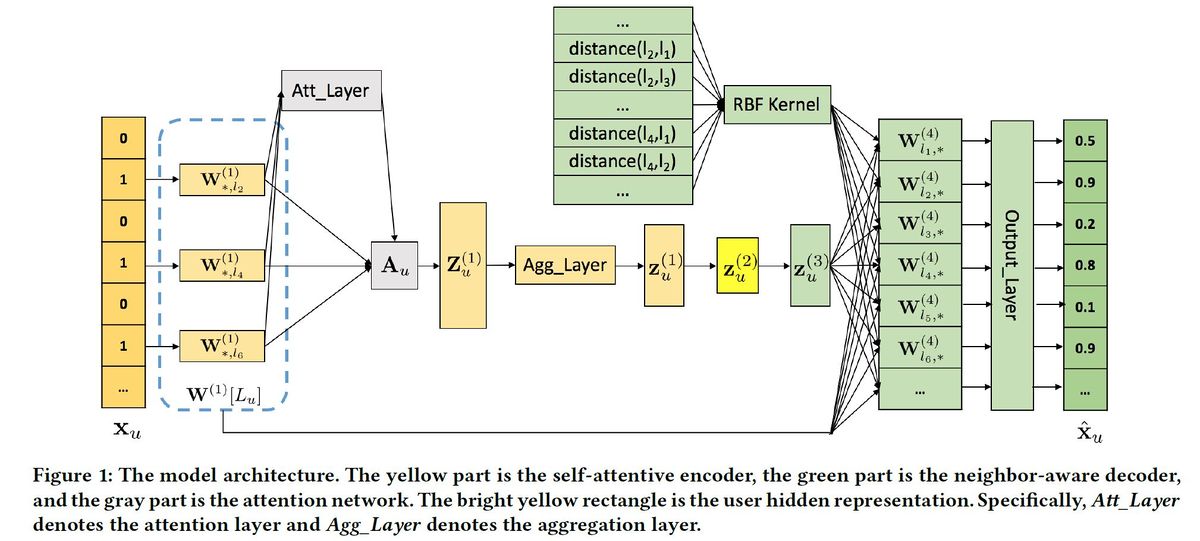
Structure

The structure of the network in this paper includes a self-attentive encoder as the input layer(yellow), and a neighbor-aware decoder as the output layer(green).

Self-Attentive Encoder

The self-attentive encoder is the input layer. It transfers the preference vector [math]\displaystyle{ x_u }[/math] to hidden representation [math]\displaystyle{ A_u }[/math] using weight matrix [math]\displaystyle{ W^1 }[/math] and the activation function [math]\displaystyle{ softmax }[/math] and [math]\displaystyle{ tanh }[/math]. The 0's and 1's in [math]\displaystyle{ x_u }[/math] indicates whether the user has been to a certain POI. The weight matrix [math]\displaystyle{ W_a }[/math] assigns different weights on various features of POIs. [math]\displaystyle{ A_u }[/math] is the importance score matrix, where each column is a POI, and each row is the importance level of the [math]\displaystyle{ n }[/math] checked in POIs in one aspect.

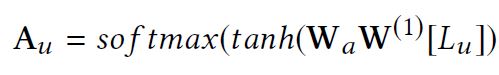
[math]\displaystyle{ \mathbf{Z}_u^{(1)} = \mathbf{A}_u \cdot (\mathbf{W}^{(1)}[L_u])^\top }[/math] is the multiplication of the importance score matrix and the POI embeddings, and represents the user from [math]\displaystyle{ d_a }[/math] aspects. [math]\displaystyle{ \mathbf{Z}_u^{(1)} }[/math] is a [math]\displaystyle{ d_a \times H_1 }[/math] matrix. The aggregation layer then combines multiple aspects that represent the user into one, so that it fits into the Neighbor-Aware decoder: [math]\displaystyle{ \mathbf{z}_u^{(1)} = a_t(\mathbf{Z}_u^{(1)\top}\mathbf{w}_t + \mathbf{b}_t) }[/math].

Neighbor-Aware Decoder

POI recommendation uses the geographical clustering phenomenon, which increases the weight of the unvisited POIs that surround the visited POIs. Also, an aggregation layer is added to the network to aggregate users’ representations from different aspects into one aspect. This means that a person who has visited a location is very likely to return to this location again in the future, so the user is recommended POIs surrounding this area. An example would be someone who has been to the UW plaza and bought Lazeez, is very likely to return to the plaza, therefore the person is recommended to try Mr. Panino's Beijing House.

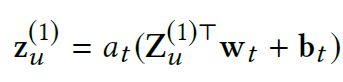
Objective Function

By minimizing the objective function, the partial derivatives with respect to all the parameters can be computed by gradient descent with backpropagation. After that, the training is complete.

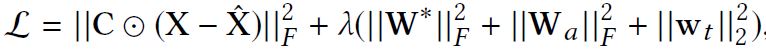
Comparative analysis

Metrics introduction

To obtain a comprehensive evaluation of the effectiveness of the model, the authors performed a thorough comparison between the proposed model and the existing major POI recommendation methods. These methods can be further broken down into three categories: traditional matrix factorization methods for implicit feedback, classical POI recommendation methods, and deep learning-based methods. Here, three key evaluation metrics were introduced as Precison@k, Recall@k, and MAP@k. Through comparing all models on three datasets using the above metrics, it is concluded that the proposed model achieved the best performance.

To better understand the comparison results, it is critical for one to understand the meanings behind each evaluation metric. Suppose the proposed model generated k recommended POIs for the user. The first metric, Precison@k, measures the percentage of the recommended POIs which the user has visited. Recall@k is also associated with the user’s behavior. However, it will measure the percentage of recommended POIs in all POIs which have been visited by the user. Lastly, MAP@k represents the mean average precision at k, where average precision is the average of precision values at all k ranks, where relevant POIs are found.

Model Comparison

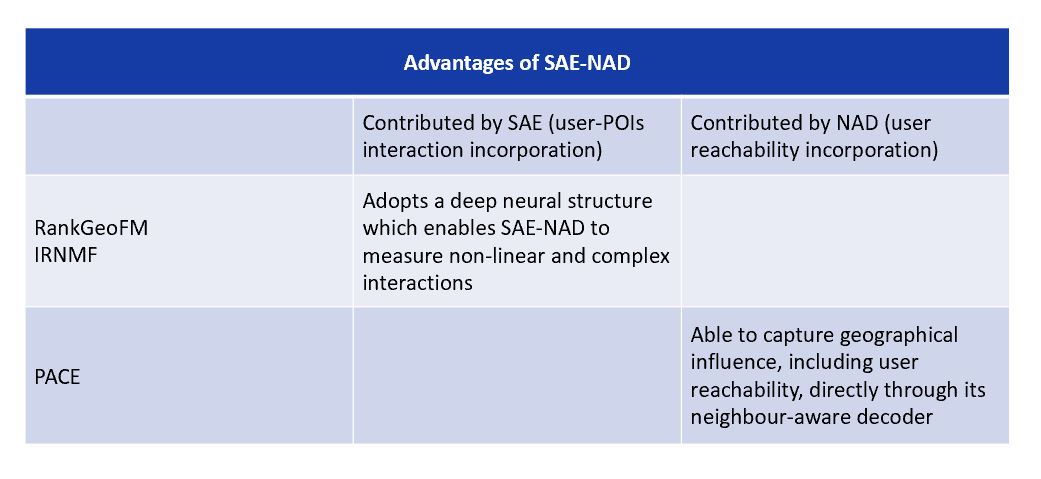
Among all models in the comparison group, RankGeoFM, IRNMF, and PACE produced the best results. Nonetheless, these models are still incomparable to our proposed model. The reasons are explained in details as follows:

Both RankGeoFM and IRNMF incorporate geographical influence into their ranking models, which is significant for generating POI recommendations. However, they are not capable of capturing non-linear interactions between users and POIs. In comparison, the proposed model, while incorporating geographical influence, adopts a deep neural structure which enables it to measure non-linear and complex interactions. As a result, it outperforms the two methods in the comparison group.

Moreover, compared to PACE, which is a deep learning-based method, the proposed model offers a more precise measurement of geographical influence. Though PACE is able to capture complex interactions, it models the geographical influence by a context graph, which fails to incorporate user reachability into the modeling process. In contrast, the proposed model is able to capture geographical influence directly through its neighbor-aware decoder, which allows it to achieve better performance than the PACE model.

Conclusion

In summary, the proposed model, namely SAE-NAD, clearly showed its advantages compared to many state-of-the-art baseline methods. Its self-attentive encoder effectively discriminates user preferences on check-in POIs, and its neighbor-aware decoder measures geographical influence precisely through differentiating user reachability on unvisited POIs. By leveraging these two components together, it can generate recommendations that are highly relevant to its users.

Critiques

Besides developing the model and conducting a detailed analysis, the authors also did very well in constructing this paper. The paper is well-written and has a highly logical structure. Definitions, notations, and metrics are introduced and explained clearly, which enables readers to follow through the analysis easily. Last but not least, both the abstract and the conclusion of this paper are strong. The abstract concisely reported the objectives and outcomes of the experiment, whereas the conclusion is succinct and precise.

This idea would have many applications, such as suggesting new restaurants to customers in the food delivery service app. Would the improvement in accuracy outweigh the increased complexity of the model when it comes to use in industry?

It would be nice if the authours could describe the extensive experiments on the real-world datasets, with different baseline methods and evaluation metrics, to demonstrate the effectiveness of the proposed model. Moreover, show the comparison result in tables vs other methodologies, both in terms of accuracy and time-efficiency. In addition, the drawbacks of this new methodology are unknown to the readers. In other words, how does this compare to the already established recommendation systems found in large scale applications utilize by companies like Netflix? Why use the proposed method over something simpler such as matrix factorization or collaborative filtering?

It would also be nice if the authors provided some more ablation on the various components of the proposed method. Even after reading some of their experiments, we do not have a clear understanding of how important each component is to the recommendation quality.

It is recommended that the author present how the encoder and the decoder help in the process by comparing different models with or without encoder and decoder.

It would have been better if the author included all figures to explain the sensitivity of parameters more elaborately. In the paper he only included plots showing effects on Gowalla and Foursquare datasets but not other datasets.

Some additional explanations can be inserted in the Objective Function part. From the paper, we can find [math]\displaystyle{ \lambda }[/math] is the regularization parameter and [math]\displaystyle{ W_a }[/math] and [math]\displaystyle{ w_t }[/math] are the learned parameters in the attention layer and aggregation layer.

References

[1] Defu Lian, Cong Zhao, Xing Xie, Guangzhong Sun, Enhong Chen, and Yong Rui. 2014. GeoMF: joint geographical modeling and matrix factorization for point-of-interest recommendation. In KDD. ACM, 831–840.

[2] Eunjoon Cho, Seth A. Myers, and Jure Leskovec. 2011. Friendship and mobility: user movement in location-based social networks. In KDD. ACM, 1082–1090.

[3] Yiding Liu, Tuan-Anh Pham, Gao Cong, and Quan Yuan. 2017. An Experimental Evaluation of Point-of-interest Recommendation in Location-based Social Networks. PVLDB 10, 10 (2017), 1010–1021.

[4] Jie Bao, Yu Zheng, David Wilkie, and Mohamed F. Mokbel. 2015. Recommendations in location-based social networks: a survey. GeoInformatica 19, 3 (2015), 525–565.

[5] Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, and Tat-Seng Chua. 2017. Neural Collaborative Filtering. In WWW. ACM, 173–182.

[6] Yifan Hu, Yehuda Koren, and Chris Volinsky. 2008. Collaborative Filtering for Implicit Feedback Datasets. In ICDM. IEEE Computer Society, 263–272.

[7] Santosh Kabbur, Xia Ning, and George Karypis. 2013. FISM: factored item similarity models for top-N recommender systems. In KDD. ACM, 659–667. [12] Diederik P. Kingma and Jimmy Ba. 2014. Adam: A Method for Stochastic Optimization. CoRR abs/1412.6980 (2014).

[8] Yong Liu,WeiWei, Aixin Sun, and Chunyan Miao. 2014. Exploiting Geographical Neighborhood Characteristics for Location Recommendation. In CIKM. ACM, 739–748

[9] Xutao Li, Gao Cong, Xiaoli Li, Tuan-Anh Nguyen Pham, and Shonali Krishnaswamy. 2015. Rank-GeoFM: A Ranking based Geographical Factorization Method for Point of Interest Recommendation. In SIGIR. ACM, 433–442.

[10] Carl Yang, Lanxiao Bai, Chao Zhang, Quan Yuan, and Jiawei Han. 2017. Bridging Collaborative Filtering and Semi-Supervised Learning: A Neural Approach for POI Recommendation. In KDD. ACM, 1245–1254.