When Does Self-Supervision Improve Few-Shot Learning?

Presented by

Arash Moayyedi

Introduction

This paper seeks to solve the generalization issues in few-shot learning by applying self-supervised learning techniques on the base dataset. Few-shot learning refers to training a classifier on minimalist datasets, contrary to the normal practice of using massive data, in hope of successfully classifying previously unseen, but related classes. Additionally, self-supervised learning aims at teaching the agent the internal structures of the images by providing it with tasks such as predicting the degree of rotation in an image. This method helps with the mentioned generalization issue, where the agent cannot distinguish the difference between newly introduced objects.

Previous Work

This work leverages few-shot learning, where we aim to learn general representations, so that when facing novel classes, the agent can differentiate between them with training on just a few samples. Many different few-shot learning methods currently exist, among which, this paper focuses on Prototypical Networks or ProtoNets for short. There is also a section of this paper that compares this model with model-agnostic meta-learner (MAML).

The other machine learning technique that this paper is based on is self-supervised learning. In this technique we find a use for unlabeled data, while labeling and maintaining massive data is expensive. The image itself already contains structural information that can be utilized. There exist many SSL tasks, such as removing a part of the data in order for the agent to reconstruct the lost part. Other methods include tasks prediction rotations, relative patch location, etc.

Method

The authors of this paper suggest a framework, as seen in Fig. 1, that combines few-shot learning with self-supervised learning. The labeled training data consists of a set of base classes in pairs of images and labels, and its domain is denoted by [math]\displaystyle{ \mathcal{D}_s }[/math]. Similarly, the domain of the images used for the self-supervised tasks is shown by [math]\displaystyle{ \mathcal{D}_{ss} }[/math]. This paper also analyzes the effects of having [math]\displaystyle{ \mathcal{D}_s = \mathcal{D}_{ss} }[/math] versus [math]\displaystyle{ \mathcal{D}_s \neq \mathcal{D}_{ss} }[/math] on the accuracy of the final few-shot learning task.

Figure 1: Suggested architecture.

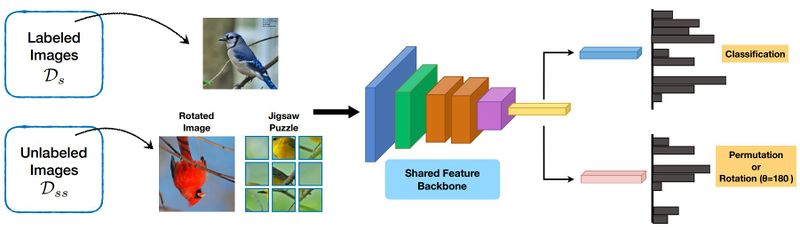
The input is connected to a feed-forward convolutional network [math]\displaystyle{ f(x) }[/math] and it is the shared backbone between the classifier [math]\displaystyle{ g }[/math] and the self-supervised target predictor [math]\displaystyle{ h }[/math]. The classification loss [math]\displaystyle{ \mathcal{L}_s }[/math] and the task prediction loss [math]\displaystyle{ \mathcal{L}_{ss} }[/math] are written as:

[math]\displaystyle{ \mathcal{L}_s := \sum_{(x_i,y_i)\in \mathcal{D}_s} \ell(g \circ f(x_i), y_i) + \mathcal{R}(f,g), }[/math]

[math]\displaystyle{ \mathcal{L}_{ss} := \sum_{x_i\in \mathcal{D}_{ss}} \ell(h \circ f(\hat{x_i}), \hat{y_i}). }[/math]

The final loss is [math]\displaystyle{ \mathcal{L} := \mathcal{L}_s + \mathcal{L}_{ss} }[/math], and thus the self-supervised losses act as a data-dependent regularizer for representation learning. The gradient updates are therefore performed based on this combined loss. It should be noted that in case [math]\displaystyle{ \mathcal{D}_s \neq \mathcal{D}_{ss} }[/math], a forward pass is done on a batch per each dataset, and the two losses are combined.

Experiments

The authors of this paper have experimented on the following datasets: Caltech-UCSD birds, Stanford cars, FGVC aircrafts, Stanford dogs, Oxford flowers, mini-ImageNet, and tiered-Imagenet. Each dataset is divided into three disjoint sets: base set for training the parameters, val set for validation, and the novel set for testing with a few examples per each class. Data augmentation has been used with all these datasets to improve the results.

Two tasks have been used for the self-supervised learning part, rotation and the Jigsaw puzzle. In the rotation task the image is rotated by an angle [math]\displaystyle{ \theta \in \{0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ}\} }[/math], which results in the input, and the target label is the index of the rotation in the list. In the Jigsaw puzzle task, the image is tiled into [math]\displaystyle{ 3\times3 }[/math] tiles and then these tiles are shuffled to produce the input image. The target is a number in range of 35 based on the hamming distance.

Results

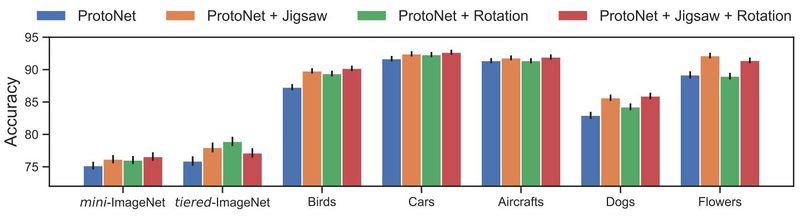
The results on 5-way 5-shot classification accuracy can be seen in Fig. 2. ProtoNet has been used as a baseline and is compared with the Jigsaw task, the rotation task, and both of them combined. The result is that the Jigsaw task always improves the result. However, the rotation task seems to not provide much improvement on the flowers and the aircraft datasets. The authors speculate that this might be because of the fact that flowers are mostly symmetrical, making the task too hard, and that the planes are usually horizontal, making the task too simple.

Figure 2: Benefits of SSL for few-shot learning tasks.

In another attempt, it is also proven that the improvements self-supervised learning provides are much higher in more difficult few-shot learning problems. As it can be observed from Fig. 3, SSL is found to be more beneficial with greyscale or low resolution images, which make the classification harder for natural and man-made objects, respectively.

Figure 3: Benefits of SSL for harder few-shot learning tasks<./div>

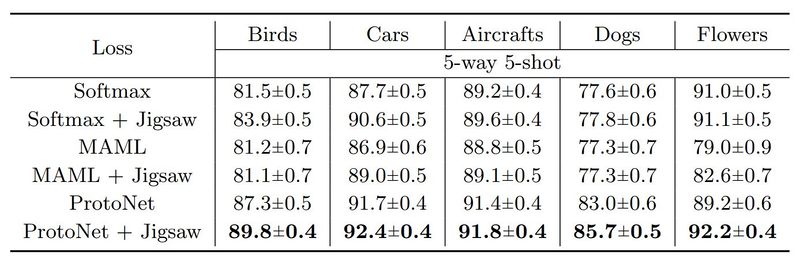
Self-supervision has also been combined with two other meta-learners in this work, MAML and a standard feature extractor trained with cross-entropy loss (softmax). Fig. 4 summarizes these results, and even though there is an accuracy gain in all scenarios (except for two), the ProtoNet + Jigsaw combination seems to work best.

Figure 4: Performance on few-shot learning using different meta-learners.

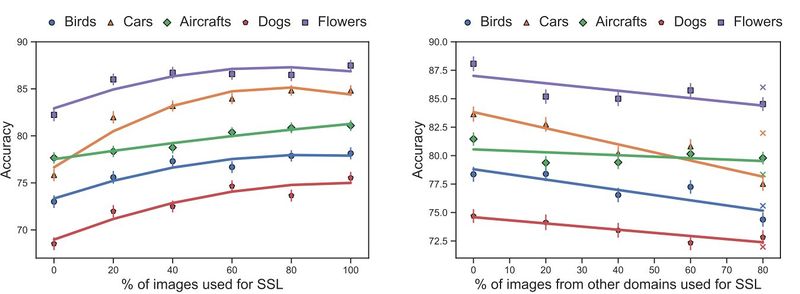
In Fig. 5 you can see the effects of size and domain of SSL on 5-way 5-shot classification accuracy. First, only 20 percent of the data is used for meta-learning. Fig. 5(a) shows the changes in the accuracy based on increasing the percent of the images, from the whole dataset, used for SSL. It is observed that increasing the size of the SSL dataset domain has a positive effect, with diminishing ends. Fig. 5(b) shows the effects of shifting the domain of the SSL dataset, by changing a percentage of the images with pictures from other datasets. This has a negative result and moreover, training with SSL on the 20 percent of the images used for meta-learning is often than increasing the size, but shifting the domain. This is shown az crosses on the chart.

Figure 5: (a) Effect of number of images on SSL. (b) Effct of domain shift on SSL.

Conclusion

The authors of this paper provide us with a great insight on the effects of using SSL as a regulizer for few-shot learning methods. It is proven that SSL is beneficial in almost every case, however, these improvements are much higher in more difficult tasks. It also shown that the dataset used for SSL should not necessarily be large. Increase the size of the mentioned dataset can possibly help, but only if the added images are from the same or a similar domain.

Critiques

The authors of this paper could have analyzed other SSL tasks in addition to the Jigsaw puzzle and the rotation task, e.g. number of objects and removed patch prediction. Moreover, comparing their work with previous works, we can see they have used mini-ImageNet with a picture size of [math]\displaystyle{ 244\times224 }[/math] in contrast to other methods that have used a $84\times84$ image size. This gives them a huge advantage, however, we still notice that other methods with smaller images have achieved higher accuracy.