Towards Deep Learning Models Resistant to Adversarial Attacks
Presented by
- Yongqi Dong
- Aden Grant
- Andrew McMurry
- Jameson Ngo
- Baizhi Song
- Yu Hao Wang
- Amy Xu
1. Introduction
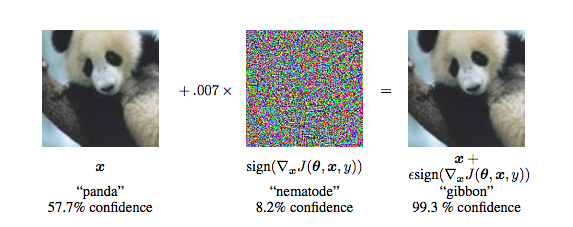
Any classifier can be tricked into giving the incorrect result. When an input is specifically designed to do this, it is called an adversarial attack. This can be done by injecting a set of perturbations to the input. These attacks are a prominent challenge for classifiers that are used for image processing and security systems because small changes to the input values that are imperceptible to the human eye can easily fool high-level neural networks. As such, resistance to adversarial attacks has become increasingly important for classifiers to have.
While there have been many approaches to defend against adversarial attacks, we can never be certain that these defenses will be able to robust against broad types of adversaries. Furthermore, these defenses can be evaded by stronger and adaptive adversaries.
Contributions
This paper uses robust optimization to explore adversarial robustness of neural networks. The authors conduct an experimental study of the saddle-point formulation which is used for adversarially training. The authors propose that we can reliably solve the saddle-point optimization problem using first-order methods, particularly project gradient descent and stochastic gradient descent, despite the problem's non-convexity and non-concavity. They explore how network capacity affects adversarial robustness and conclude that networks need larger capacity in order to be resistant to strong adversaries. Lastly, they train adversarially robust networks on MNIST and CIFAR10 using the saddle point formulation.
2. An Optimization View on Adversarial Robustness
Consider a standard classification task on data [math]\displaystyle{ x \in \mathbb{R}^d }[/math] and labels [math]\displaystyle{ y \in [1,...,k] }[/math], assumed to have underlying distribution [math]\displaystyle{ D }[/math]. Based a given loss function [math]\displaystyle{ L(\theta,x,y) }[/math] (e.g. the cross-entropy loss), the goal is to find the model parameters [math]\displaystyle{ \theta \in \mathbb{R}^p }[/math] that minimize the empirical risk of misclassification. In other words, the problem is:
[math]\displaystyle{ \min_{\theta} \mathbb{E}_{(x,y) \sim D} [L(\theta,x,y)] }[/math]
However, empirical risk minimization may not result in models that are robust against adversaries. To produce robust models, we instead define conditions that the model must satisfy and train the model according to those conditions. We describe the set of attacks that our model must be robust against by considering a set of perturbations [math]\displaystyle{ S \subseteq \mathbb{R}^d }[/math] for each data point [math]\displaystyle{ x }[/math]. This gives a set of data points with similar properties to [math]\displaystyle{ x }[/math], for example, the [math]\displaystyle{ l_{\infty} }[/math]-ball around x, which we focus on in this paper.
We then define an augmented classification algorithm based on perturbed input data rather than the natural data. Our goal then becomes finding the model parameters [math]\displaystyle{ \theta \in \mathbb{R}^p }[/math] which minimize the expected loss calculated on perturbed data. This results in a saddle point problem:
[math]\displaystyle{ \min_{\theta} \mathbb{E}_{(x,y) \sim D} [\max_{\delta \in S} L(\theta,x+\delta,y)] }[/math]
We rewrite this as [math]\displaystyle{ \min_{\theta} \rho (\theta) }[/math] where [math]\displaystyle{ \rho (\theta) }[/math] is the adversarial loss of the network; this problem thus becomes the primary topic of this paper. The saddle point problem has two components:
- Inner maximization: [math]\displaystyle{ \qquad \max_{\delta \in S} L(\theta,x+\delta,y) }[/math]
This involves finding the adversarial version of input data x that results the highest loss, which is equivalent to building an attack against the network. - Outer minimization: [math]\displaystyle{ \qquad \min_{\theta} \rho (\theta) }[/math]
This involves finding model parameters that minimize the above adversarial loss, i.e. training the network to be adversarially robust.
3. Adversarially Robust Networks
Obtaining the outer minimization of the saddle point formulation [math]\displaystyle{ \min_{\theta} \rho (\theta) }[/math] guarantees that all perturbations result in smallest adversarial loss possible based on the attack. Stochastic gradient descent (SGD) is used to solve the outer minimization problem by obtaining the gradients [math]\displaystyle{ \nabla_\theta \rho(\theta) }[/math], which are computed at the maximizer of the inner maximization problem.
Solutions for the inner maximization are used as known adversarial attacks on the neural network.
Inner Maximization
Based on prior research, the maximizers [math]\displaystyle{ \delta \in S }[/math] of [math]\displaystyle{ \rho(\delta) }[/math] are obtained by using projected gradient descent (PGD). Since the inner maximization is non-concave, the global maximizer cannot be found using PGD (instead, PGD will converge to local maxima). However, the paper’s findings conclude that PGD can be used in practice to solve the inner maximization problem using first-order methods.
Applying Danskin’s theorem on a subset [math]\displaystyle{ S' \in S }[/math] where the local maximum is the global maximum of the region [math]\displaystyle{ S' }[/math] gives the gradient corresponding to the descent direction for the saddle point problem when the adversary is constrained to [math]\displaystyle{ S' }[/math]. The authors also find that the local maxima are widely spread apart within [math]\displaystyle{ x_i+S }[/math] but tended to have similar loss values for both normally and adversarially trained networks.
Outer Minimization
Since distribution [math]\displaystyle{ D }[/math] is unknown, the gradients and [math]\displaystyle{ \rho(\theta) }[/math] are obtained using sampled input points, i.e. for the case of a single random example [math]\displaystyle{ x }[/math] with label [math]\displaystyle{ y }[/math], we have the problem:
[math]\displaystyle{ L }[/math] is assumed to be continuously differentiable for [math]\displaystyle{ \theta }[/math], and Danskin’s theorem is used to obtained the direction of descent. Discontinuity when using ReLU activations was assumed to not be an issue as the set of discontinuities had a measure of zero, and thus these points of discontinuity would never be encountered. Using the gradients [math]\displaystyle{ \nabla_\theta \rho(\theta) }[/math] obtained with SGD, the loss of the saddle point problem is reduced during training. Thus, the saddle point optimization problem can be solved and classifiers can be trained to be adversarially robust.
4. Experiments
Amy
5. First-Order Adversaries
Since all local maxima founded by PGD tended to have similar loss values, this suggests that it is very unlikely that any other first-order adversary will yield a local maxima with a significantly lower loss value than PGD. This is seen experimentally: other adversaries with significantly lower loss values were not found even after a large amount of restarts.
The authors also experimentally found that a network trained to be robust against PGD adversaries also became robust against various other first-order adversaries. This result, along with the fact that the vast majority of optimization problems in machine learning are solved using first-order methods suggest that the saddle point formulation to adversarially train networks will encompass all current approaches to achieve adversarial robustness.
Transfer attacks
Transfer attacks are adversarial attacks that do not have direct access to the classifier. Although these attacks evaluate the classifier without gradient feedback, the gradient of the network can be estimated with finite differences. Thus, first-order attacks are relevant to use in order to train against these attacks. The paper found that increasing network capacity and the adversary strength that the network is trained against improved resistance to transfer attacks. It also found that the models that were resistant to first-order attacks were more resistant to transfer attacks.
6. Related Work
Amy