Towards Deep Learning Models Resistant to Adversarial Attacks
Presented by
- Yongqi Dong
- Aden Grant
- Andrew McMurry
- Jameson Ngo
- Baizhi Song
- Yu Hao Wang
- Amy Xu
1. Introduction
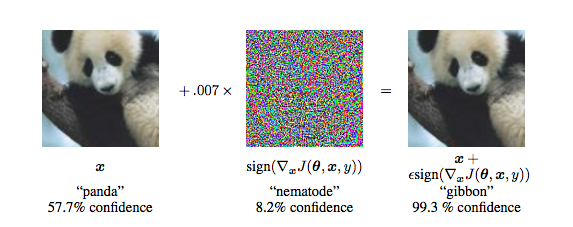
Any classifier can be tricked into giving the incorrect result. When an input is specifically designed to do this, it is called an adversarial attack. This can be done by injecting a set of perturbations to the input. These attacks are a prominent challenge for classifiers that are used for image processing and security systems because small changes to the input values that are imperceptible to the human eye can easily fool high-level neural networks. As such, resistance to adversarial attacks has become increasingly important for classifiers to have.
While there have been many approaches to defend against adversarial attacks, we can never be certain that these defenses will be able to robust against broad types of adversaries. Furthermore, these defenses can be evaded by stronger and adaptive adversaries.
Contributions
This paper uses robust optimization to explore adversarial robustness of neural networks. The authors conduct an experimental study of the saddle-point formulation which is used for adversarially training. The authors propose that we can reliably solve the saddle-point optimization problem using first-order methods, particularly project gradient descent (PGD) and stochastic gradient descent (SGD), despite the problem's non-convexity and non-concavity. They explore how network capacity affects adversarial robustness and conclude that networks need larger capacity in order to be resistant to strong adversaries. Lastly, they train adversarially robust networks on MNIST and CIFAR10 using the saddle point formulation.
2. An Optimization View on Adversarial Robustness
Consider a standard classification task on data [math]\displaystyle{ x \in \mathbb{R}^d }[/math] and labels [math]\displaystyle{ y \in [1,...,k] }[/math], assumed to have underlying distribution [math]\displaystyle{ D }[/math]. Based a given loss function [math]\displaystyle{ L(\theta,x,y) }[/math] (e.g. the cross-entropy loss), the goal is to find the model parameters [math]\displaystyle{ \theta \in \mathbb{R}^p }[/math] that minimize the empirical risk of misclassification. In other words, the problem is:
[math]\displaystyle{ \min_{\theta} \mathbb{E}_{(x,y) \sim D} [L(\theta,x,y)] }[/math]
However, empirical risk minimization may not result in models that are robust against adversaries. To produce robust models, we instead define conditions that the model must satisfy and train the model according to those conditions. We describe the set of attacks that our model must be robust against by considering a set of perturbations [math]\displaystyle{ S \subseteq \mathbb{R}^d }[/math] for each data point [math]\displaystyle{ x }[/math]. This gives a set of data points with similar properties to [math]\displaystyle{ x }[/math], for example, the [math]\displaystyle{ l_{\infty} }[/math]-ball around x, which we focus on in this paper.
We then define an augmented classification algorithm based on perturbed input data rather than the natural data. Our goal then becomes finding the model parameters [math]\displaystyle{ \theta \in \mathbb{R}^p }[/math] which minimize the expected loss calculated on perturbed data. This results in a saddle point problem:
[math]\displaystyle{ \min_{\theta} \mathbb{E}_{(x,y) \sim D} [\max_{\delta \in S} L(\theta,x+\delta,y)] }[/math]
We rewrite this as [math]\displaystyle{ \min_{\theta} \rho (\theta) }[/math] where [math]\displaystyle{ \rho (\theta) }[/math] is the adversarial loss of the network; this problem thus becomes the primary topic of this paper. The saddle point problem has two components:
- Inner maximization: [math]\displaystyle{ \qquad \max_{\delta \in S} L(\theta,x+\delta,y) }[/math]
This involves finding the adversarial version of input data x that results the highest loss, which is equivalent to building an attack against the network. - Outer minimization: [math]\displaystyle{ \qquad \min_{\theta} \rho (\theta) }[/math]
This involves finding model parameters that minimize the above adversarial loss, i.e. training the network to be adversarially robust.
4. Experiments
Amy
6. Related Work
Amy