summary
XGBoost: A Scalable Tree Boosting System
Presented by
Jiang, Cong
Song, Ziwei
Ye, Zhaoshan
Zhang, Wenling
Introduction
In recent years, XGBoost has been the most popular tool in Kaggle, as well as other machine learning and data mining challenges. The main reason to its success is that this tree boosting system is highly scalable , which means it could be used to solve a variety of different problems.
This paper is written by XGBoost's father, Tianqi Chen. It gives us an overview on how he used algorithmic optimizations as well as some important systems to develop XGBoost. He explained it in the following manner:
1. Based on gradient tree boosting algorithm as well as using shrinkage and feature subsampling to prevent overfitting, Chen introduced an end-to-end tree boosting system.
2.
Tree Boosting
Regularized Learning Objective
Suppose the given data set has m features and n examples. A tree ensemble model uses K additive functions to predict the output.
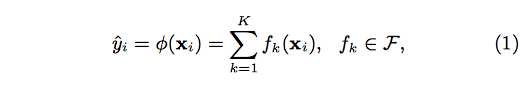
where F is the space of regression trees(CART). The author suggests the following regularized objective function to make improvements comparing to gradient boosting
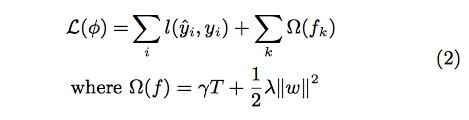
Regression tree contains continuous scores on each leaf, which is different with decision trees we have learned in class. The following 2 figures represent how to use the decision rules in the trees to classify it into the leaves and calculate the final prediction by summing up the score in the corresponding leaves.
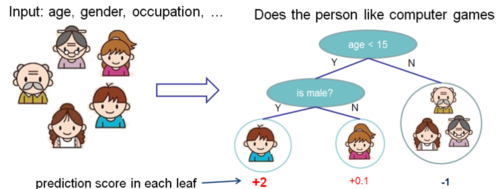
Figure 0: Prediction Score of Tree Structure.
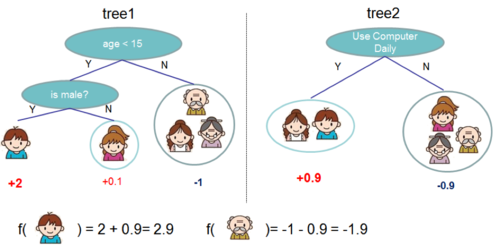
Figure 1: Tree Ensemble Model. The final prediction for a given example is the sum of predictions from each tree.
Gradient Tree Boosting
The tree ensemble model (Equation 2.) is trained in an additive manner. We need to add a new [math]\displaystyle{ f }[/math] to our objective.
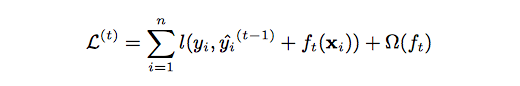
After applying the second-order Taylor expansion to the above formula and removing constant terms, we can finally have
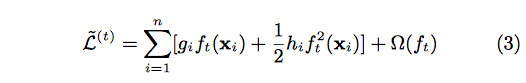
Define [math]\displaystyle{ I_{j} = \{i| q(X_{i}) \} }[/math] As the instance set of leaf j. We can rewrite Equation (3) as
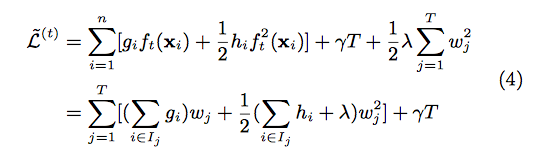
By computing the optimal weight and corresponding optimal value, we can use following equation as the scoring function which can measure the quality of a tree structure. Lower score means better tree structure.
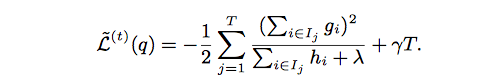
The following figure shows an example how this score is calculated.
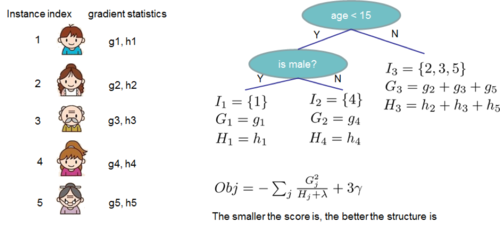
Figure 2: Structure Score Calculation. We only need to sum up the gradient and second order gradient statistics on each leaf, then apply the scoring formula to get the quality score.
Normally it is impossible to enumerate all the possible tree structures. Assume [math]\displaystyle{ I_{L} }[/math] and [math]\displaystyle{ I_{R} }[/math] are the instance sets of left and right nodes after the split, and [math]\displaystyle{ I = I_{L} + I_{R} }[/math]. Then the loss reduction after the split is given by
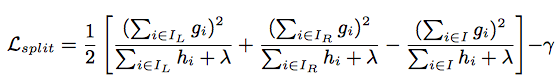
Split Finding Algorithms
System Design
Related Works
End to End Evaluations
Results
Conclusion
Criticisms
Source
**Sample format
Recurrent neural networks are a variation of deep neural networks that are capable of storing information about previous hidden states in special memory layers.<ref name=lstm> Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory." Neural computation 9.8 (1997): 1735-1780. </ref> Unlike feed forward neural networks that take in a single fixed length vector input and output a fixed length vector output, recurrent neural networks can take in a sequence of fixed length vectors as input, because of their ability to store information and maintain a connection between inputs through this memory layer. By comparison, previous inputs would have no impact on current output for feed forward neural networks, whereas they can impact current input in a recurrent neural network. (This paper used the LSTM formulation from Graves<ref name=grave> Graves, Alex. "Generating sequences with recurrent neural networks." arXiv preprint arXiv:1308.0850 (2013). </ref>)
Where [math]\displaystyle{ \,S }[/math] is the base/source sentence, [math]\displaystyle{ \,T }[/math] is the paired translated sentence and [math]\displaystyle{ \,T_r }[/math] is the total training set. This objective function is to maximize the log probability of a correct translation [math]\displaystyle{ \,T }[/math] given the base/source sentence [math]\displaystyle{ \,S }[/math] over the entire training set. Once the training is complete, translations are produced by finding the most likely translation according to LSTM:
- [math]\displaystyle{ \hat{T} = \underset{T}{\operatorname{arg\ max}}\ p(T|S) }[/math]
It has been showed that Long Short-Term Memory recurrent neural networks have the ability to generate both discrete and real-valued sequences with complex, long-range structure using next-step prediction <ref name=grave>
Reference
</ref>.