LightRNN: Memory and Computation-Efficient Recurrent Neural Networks
Introduction
The study of natural language processing has been around for more than fifty years. It begins in 1950s which the specific field of natural language processing (NLP) is still embedded in the subject of linguistics (Hirschberg & Manning, 2015). After the emergence of strong computational power, computational linguistics began to evolve and gradually branch out to various applications in NLP, such as text classification, speech recognition and question answering (Brownlee, 2017). Computational linguistics or natural language processing is usually defined as “subfield of computer science concerned with using computational techniques to learn, understand, and produce human language content” (Hirschberg & Manning, 2015, p. 261).
With the development in deep neural networks, one type of neural network, namely recurrent neural networks (RNN) have preformed significantly well in many natural language processing tasks. The reason is that nature of RNN takes into account the past inputs as well as the current input without resulting in vanishing or exploding gradient. More detail of how RNN works in the context of NLP will be discussed in the section of NLP using RNN. However, one limitation of RNN used in NLP is its enormous size of input vocabulary. This will result in a very complex RNN model with too many parameters to train and makes the training process both time and memory-consuming. This serves as the major motivation for this paper’s authors to develop a new technique utilized in RNN, which is particularly efficient at processing large size of vocabulary in many NLP tasks, namely LightRNN.
Natural Language Processing (NLP) Using Recurrent Neural Network (RNN)
In language modelling, researchers used to represent words by arbitrary codes, such as “Id143” is the code for “dog” (“Vector Representations of Words,” 2017). Such coding of words is completely random, and it loses the meaning of the words and (more importantly) connection with other words. Nowadays, one-hot representation of words is commonly used, in which a word is represented by a vector of numbers and the dimension of the vector is corresponding to the size of the word. In RNN, all words in the vocabulary are coded using one-hot representation and then mapped to an embedding vector (Li, Qin, Yang, Hu, & Liu, 2016). Such embedding vector is “a continuous vector space where semantically similar words are mapped to nearby points” (“Vector Representations of Words” 2017, para. 6). Popular RNN structure used in NLP task is long short-term memory (LSTM). In order to predict the probability of the next word, the last hidden layer of the network needs to calculate the probability distribution of all other words in the vocabulary. Lastly, an activation function (commonly, softmax function) is used to select the next word with the highest probability. This method has 3 major limitations:
1. Memory Constraint
When input vocabulary contains enormous amount of unique words, which is very common in various NLP tasks, the size of model becomes very large. This means the number of trainable parameters is very big, which makes it difficult to fit such model on a regular GPU device.
2. Computationally Heavy to Train
As previously mentioned, probability distribution of all other words in the vocabulary needs to be computed to determine what predicted word it would be. When the size of the vocabulary is large, such calculation can be computationally heavy.
3. Low Generalizability
Due to the memory and computation-consuming process of RNN applied in NLP tasks, mobile devices cannot usually handle such algorithm, which makes it undesirable and limits its usage.
LightRNN Structure
The authors of the paper proposed a new structure that effectively reduces the size of the model by arranging all words in the vocabulary into a word table, which is referred as “2-Component (2C) shared embedding for word representation”. Thus, a word is indexed by its location in such table, which in terms is characterized by the corresponding row and column components. Each row and column component are unique row vector and column vector respectively. By organizing each word in the vocabulary in this manner, multiple words can share the same row component or column component and it can reduce the number of trainable parameters significantly. The next question is how to construct such word table. More specifically, how to allocate each word in the vocabulary to different positions so that semantically similar words are in the same row or column. The authors proposed a bootstrap method to solve this problem. Essentially, we first randomly distribute words into the table. Then, we let the model “learn” better position of each word by minimizing training error. By repeating this process, each word can be allocated to a particular position within the table so that similar words share common row or column components. More details of those 2 parts of LightRNN structure will be discussed in the following sections.
There are 2 major benefits of the proposed technique:
1. Computationally efficient
The name “LightRNN” is to illustrate the small model size and fast training speed. Because of these features of the new RNN architecture, it’s possible to launch such model onto regular GPU and other mobile devices.
2. Higher scalability
The authors briefly explained this algorithm is scalable because if parallel-computing is needed to train such model, the difficulty of combining smaller models is low.
The key aspect of LightRNN structure is its innovative method of word representation, namely 2-Component Shared Embedding. All words in the vocabulary is organized into a table with row components and column components. Each pair of element in a row component and a column component is corresponding to a unique word in the vocabulary. For instance, the [math]\displaystyle{ i^{th} }[/math] row and [math]\displaystyle{ j^{th} }[/math] column are the row and column indexes for [math]\displaystyle{ X_{ij} }[/math]. As shown in the following graph, [math]\displaystyle{ x_{1} }[/math] is corresponding to the words “January”. In 2C shared embedding table, it’s indexed by 2 elements: [math]\displaystyle{ x^{r}_{1} }[/math] and [math]\displaystyle{ x^{c}_{1} }[/math] where the subscript indicates which row component and column component this word belongs to. Ideally, words that share similar semantic features should be assigned to the same row or column. The shared embedding word table in Figure 1 serves as a good example: the word “one” and “January” are assigned to the same column, while the word “one” and “two” are allocated to the same row.
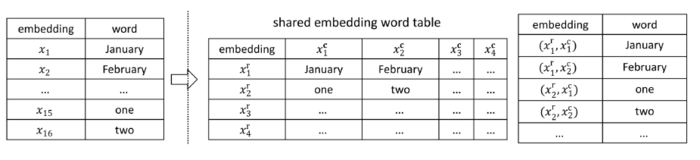
The main advantage of using such word representation is it reduces the number of vector/element needed for input word embedding. For instance, if there are 25 unique words in the vocabulary, the number of vectors to represent all the words is 10, namely 5 row vectors/elements and 5 column vectors/elements. Therefore, the shared embedding word table is a 5 by 5 matrix. In general, the formula for calculating number of vector/element needed to represent |V| words is [math]\displaystyle{ 2\sqrt{|V|} }[/math].
After constructing such word representation table, those 2-component shared embedding matrices are fed into the recurrent neural network. The following Figure 2 demonstrates a portion of LightRNN structure (left) with comparison with the regular RNN (right). Compared to regular RNN where a single input [math]\displaystyle{ x_{t-1} }[/math] is fed into the network each time, 2 elements of a single input [math]\displaystyle{ x_{t-1} }[/math]: [math]\displaystyle{ x^{r}_{t-1} }[/math] and [math]\displaystyle{ x^{c}_{t-1} }[/math] are fed into LightRNN.
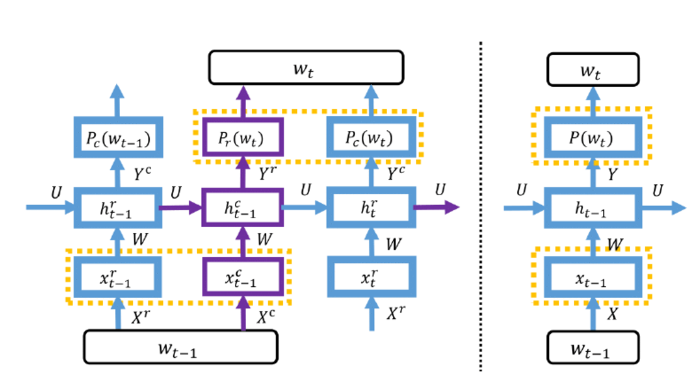
As mentioned before, the last hidden layer will produce the probabilities of [math]\displaystyle{ word_{t} }[/math]. Based on the diagram below, the following formulas are used: Let n = dimension/length of a row input vector, m = dimension/length of a column input vector, [math]\displaystyle{ X^{c}, X^{r} \in \mathbb{R}^{n \times \sqrt{|V|}} }[/math] denotes the input-embedding matrices:
- row vector [math]\displaystyle{ x^{r}_{t-1} \in \mathbb{R}^n }[/math]
- column vector [math]\displaystyle{ x^{c}_{t-1} \in \mathbb{R}^n }[/math]
Let [math]\displaystyle{ h^{c}_{t-1}, h^{r}_{t-1} \in \mathbb{R}^m }[/math] denotes the two hidden layers:
- [math]\displaystyle{ h^{c}_{t-1} = f(W x_{t-1}^{c} + U h_{t-1}^{r} + b) }[/math]
- [math]\displaystyle{ h^{r}_{t} = f(W x_{t}^{r} + U h_{t-1}^{c} + b) }[/math]
where [math]\displaystyle{ W \in \mathbb{R}^m \times n }[/math], [math]\displaystyle{ U \in \mathbb{R}^m \times n }[/math] & [math]\displaystyle{ b \in \mathbb{R}^m }[/math] and [math]\displaystyle{ f }[/math] is a nonlinear activation function
The final step in LightRNN is to calculate [math]\displaystyle{ P_{r}(w_{t}) }[/math] and [math]\displaystyle{ P_{c}(w_{t}) }[/math] , which means the probability of a word w at time t, using the following formulas:
- [math]\displaystyle{ P_{r}(w_t) = \frac{exp(h_{t-1}^{c} y_{r(w)}^{r})}{\sum\nolimits_{i \in S_r} exp(h_{t-1}^{c} y_{i}^{r}) } }[/math]
- [math]\displaystyle{ P_{c}(w_t) = \frac{exp(h_{t}^{r} y_{c(w)}^{c})}{\sum\nolimits_{i \in S_r} exp(h_{t}^{r} y_{i}^{c}) } }[/math]
- [math]\displaystyle{ P(w_t) = P_{r}(w_t) P_{c}(w_t) }[/math]
where
- [math]\displaystyle{ r(w) }[/math] = row index of word w
- [math]\displaystyle{ c(w) }[/math] = column index of word w
- [math]\displaystyle{ y_{i}^{r} \in \mathbb{R}^m }[/math] = i-th vector of [math]\displaystyle{ Y^r \in \mathbb{R}^{m \times \sqrt{|V|}} }[/math]
- [math]\displaystyle{ y_{i}^{c} \in \mathbb{R}^m }[/math] = i-th vector of [math]\displaystyle{ Y^c \in \mathbb{R}^{m \times \sqrt{|V|}} }[/math]
- [math]\displaystyle{ S_r }[/math] = the set of rows of the word table
- [math]\displaystyle{ S_c }[/math] = the set of columns of the word table
Essentially, in LightRNN, the prediction of the word at time t ([math]\displaystyle{ w_t }[/math]) based on word at time t-1 ([math]\displaystyle{ w_{t-1} }[/math]) is achieved by selecting the index [math]\displaystyle{ r }[/math] and [math]\displaystyle{ c }[/math] with the highest probabilities [math]\displaystyle{ P_{r}(w_t) }[/math], [math]\displaystyle{ P_{c}(w_t) }[/math]. Then, the probability of each word is computed based on the multiplication of [math]\displaystyle{ P_{r}(w_t) }[/math] and [math]\displaystyle{ P_{c}(w_t) }[/math].
Part III: Bootstrap for Word Allocation
As mentioned before, the major innovative aspect of LightRNN is the development of 2-component shared embedding. Such structure can be used in building a recurrent neural network called LightRNN. However, how should such work table representation be constructed is the key part of building a successful LightRNN model. In this section, the procedures of constructing 2C shared embedding structure is explained. The fundamental idea is using bootstrap method by minimizing a loss function (namely, negative lo-likelihood function). The detailed procedures are described as the following:
Step 1: First, all words in a vocabulary are randomly assigned to individual position within the word table.
Step 2: Train LightRNN model based on word table produced in step 1 until certain criteria are met.
Step 3: By fixing the training results of input and output embedding matrices (W & U) from step 2, adjust the position of words by minimizing the loss function over all the words. Then, repeat from step 2.
The authors presented the overall loss function for word w moving to position [i, j] using a negative log-likelihood function (NLL) as the following:
[math]\displaystyle{ NLL = \sum\limits_{i=1}^T -logP(w_t) = \sum\limits_{i=1}^T -log[P_{r}(w_t) P_{c}(w_t)] = \sum\limits_{i=1}^T -log[P_{r}(w_t)] – log[P_{c}(w_t)] = \sum\limits_{w=1}^{|V|} NLL_w }[/math]
where [math]\displaystyle{ NLL_w }[/math] is the negative log-likelihood of a word w.
Since in 2-component shared embedding structure, a word (w) is represented by one row vector and one column vector, [math]\displaystyle{ NLL_w }[/math] can be rewritten as [math]\displaystyle{ l(w, r(w), c(w)) }[/math] where [math]\displaystyle{ r(w) }[/math] and [math]\displaystyle{ c(w) }[/math] are the position index of word w in the word table. Next, the authors defined 2 more terms to explain the meaning of [math]\displaystyle{ NLL_w }[/math]: [math]\displaystyle{ l_r(w,r(w)) }[/math] and [math]\displaystyle{ \gt l_c(w,c(w)) }[/math], namely the row component and column component of [math]\displaystyle{ l(w, r(w), c(w)) }[/math]. The above can be summarised by the following formulas:
[math]\displaystyle{ NLL_w = \sum\limits_{t \in S_w} -logP(w_t) = l(w, r(w), c(w)) }[/math]
[math]\displaystyle{ = \sum\limits_{t \in S_w} -logP_r(w_t) + \sum\limits_{t \in S_w} -logP_c(w_t) = l_r(w,r(w)) + l_c(w,c(w)) }[/math]
[math]\displaystyle{ = \sum\limits_{t \in S_w} -log (\frac{exp(h_{t-1}^{c} y_{i}^{r})}{\sum\nolimits_{k} exp(h_{t-1}^{c} y_{i}^{k})}) + \sum\limits_{t \in S_w} -log (\frac{exp(h_{t}^{r} y_{j}^{c})}{\sum\nolimits_{k} exp(h_{t}^{r} y_{k}^{c}) }) }[/math]
where [math]\displaystyle{ S_w }[/math] is the set of all possible positions within the word table
In summary, the overall loss function for word w to move to position [i, j] is the sum of its row loss and column loss of moving to position [i, j]. Therefore, total loss of moving to position [i, j] [math]\displaystyle{ l(w, i, j) = l_r(w, i) + l_c(w, j) }[/math]. Thus, to update the table by reallocating each word, we are looking for position [i, j] for each word w that minimize the total loss function, mathematically written as for the following:
[math]\displaystyle{ \min\limits_{a} \sum\limits_{w,i,j} l(w,i,j)a(w,i,j) }[/math] such that
[math]\displaystyle{ \sum\limits_{(i,j)} a(w,i,j) = 1 \space \forall w \in V, \sum\limits_{(w)} a(w,i,j) = 1 \space \forall i \in S_r, j \in S_j }[/math]
[math]\displaystyle{ a(w,i,j) \in {0,1}, \forall w \in V, i \in S_r, j \in S_j }[/math]
where [math]\displaystyle{ a(w,i,j) =1 }[/math] indicates moving word w to position [i, j]