extracting and Composing Robust Features with Denoising Autoencoders
Introduction
This Paper explores a new training principle for unsupervised learning of a representation based on the idea of making the learned representations robust to partial corruption of the input pattern. This approach can be used to train autoencoders, and these denoising autoencoders can be stacked to initialize deep architectures. The algorithm can be motivated from a manifold learning and information theoretic perspective or from a generative model perspective. The proposed system is similar to a standard auto-encoder, which is trained with the objective function to learn a hidden representation which allows it to reconstruct its input. The difference between these two models is that the model is trained to reconstruct the original input from a corrupted version, generated by adding random noise to the data. This will result in extracting useful features.
Motivation
The approach is based on the use of an unsupervised training criterion to perform a layer-by-layer initialization. The procedure is as follows : Each layer is at first trained to produce a higher level (hidden) representation of the observed patterns, based on the representation it receives as input from the layer below, by optimizing a local unsupervised criterion. Each level produces a representation of the input pattern that is more abstract than the previous level’s, because it is obtained by composing more operations. This initialization yields a starting point, from which a global fine-tuning of the model’s parameters is then performed using another training criterion appropriate for the task at hand.
This process gives better solutions than the one obtained by random initializations
The Denoising Autoencoder
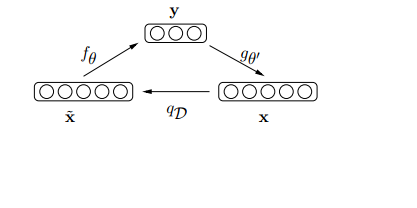
A Denoising Autoencoder reconstructs a clean “repaired” input from a corrupted, partially destroyed one. This is done by first corrupting the initial input [math]\displaystyle{ x }[/math] to get a partially destroyed version [math]\displaystyle{ \tilde{x} }[/math] by means of a stochastic mapping. This means that the autoencoder must learn to compute a representation that is informative of the original input even when some of its elements are missing. This technique was inspired by the ability of humans to have an appropriate understanding of their environment even in situations where the available information is incomplete (e.g. when looking at an object that is partly occluded). In this paper the noise is added by randomly zeroing a fixed number, [math]\displaystyle{ v_d }[/math], of components and leaving the rest untouched. This is similar to salt noise in images where we see random white background areas in an image.
As shown in the figure below, the clean input [math]\displaystyle{ x }[/math] is mapped to some corrupted version according to some conditional distribution [math]\displaystyle{ q_D(\sim{x}|x) }[/math]. The corrupted version is then mapped to some informative domain [math]\displaystyle{ y }[/math], and the autoencoder then attempts to reconstruct the clean version [math]\displaystyle{ x }[/math] from [math]\displaystyle{ y }[/math]. Thus the objective function can be described as
![]()
The objective function minimized by
stochastic gradient descent becomes:
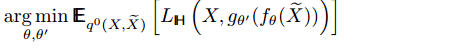
where the loss function is the cross entropy of the model The denoising autoencoder can be shown in the figure as
It is important to note that usually the dimensionality of the hidden layer needs to be less than the input/output layer in order to avoid the trivial solution of identity mapping, but in this case that is not a problem since randomly zeroing out numbers causes the identity map to fail. This forces the network to learn a more abstract representation of the data regardless of the relative sizes of the layers.
Layer-wise Initialization and Fine Tuning
While training the denoising autoencoder k-th layer used as input for the (k + 1)-th, and the (k + 1)-th layer trained after the k-th has been trained. After a few layers have been trained, the parameters are used as initialization for a network optimized with respect to a supervised training criterion. This greedy layer-wise procedure has been shown to yield significantly better local minima than random initialization of deep networks, achieving better generalization on a number of tasks.
Analysis of the Denoising Autoencoder
Manifold Learning Perspective
The process of mapping a corrupted example to an uncorrupted one can be visualized in Figure 2, with a low-dimensional manifold [math]\displaystyle{ \mathcal{M} }[/math] near which the data concentrate. We learn a stochastic operator [math]\displaystyle{ p(X|\tilde{X}) }[/math] that maps an [math]\displaystyle{ \tilde{X} }[/math] to an [math]\displaystyle{ X\, }[/math].
Since the corrupted points [math]\displaystyle{ \tilde{X} }[/math] will likely not be on [math]\displaystyle{ \mathcal{M} }[/math], the learned map [math]\displaystyle{ p(X|\tilde{X}) }[/math] is able to determine how to transform points away from [math]\displaystyle{ \mathcal{M} }[/math] into points on [math]\displaystyle{ \mathcal{M} }[/math].
The denoising autoencoder can thus be seen as a way to define and learn a manifold. The intermediate representation [math]\displaystyle{ Y = f(X) }[/math] can be interpreted as a coordinate system for points on the manifold (this is most clear if we force the dimension of [math]\displaystyle{ Y }[/math] to be smaller than the dimension of [math]\displaystyle{ X }[/math]). More generally, one can think of [math]\displaystyle{ Y = f(X) }[/math] as a representation of [math]\displaystyle{ X }[/math] which is well suited to capture the main variations in the data, i.e., on the manifold. When additional criteria (such as sparsity) are introduced in the learning model, one can no longer directly view [math]\displaystyle{ Y = f(X) }[/math] as an explicit low-dimensional coordinate system for points on the manifold, but it retains the property of capturing the main factors of variation in the data.
Stochastic Operator Perspective
The denoising autoencoder can also be seen as corresponding to a semi-parametric model that can be sampled from. Define the joint distribution as follows:
- [math]\displaystyle{ p(X, \tilde{X}) = p(\tilde{X}) p(X|\tilde{X}) = q^0(\tilde{X}) p(X|\tilde{X}) }[/math]
from the stochastic operator [math]\displaystyle{ p(X | \tilde{X}) }[/math], with [math]\displaystyle{ q^0\, }[/math] being the empirical distribution.
Using the Kullback-Leibler divergence, defined as:
- [math]\displaystyle{ \mathbb{D}_{KL}(p|q) = \mathbb{E}_{p(X)} \left(\log\frac{p(X)}{q(X)}\right) }[/math]
then minimizing [math]\displaystyle{ \mathbb{D}_{KL}(q^0(X, \tilde{X}) | p(X, \tilde{X})) }[/math] yields the originally-formulated denoising criterion. Furthermore, as this objective is minimized, the marginals of [math]\displaystyle{ \,p }[/math] approach those of [math]\displaystyle{ \,q^0 }[/math], i.e. [math]\displaystyle{ p(X) \rightarrow q^0(X) }[/math]. Then, if [math]\displaystyle{ \,p }[/math] is expanded in the following way:
- [math]\displaystyle{ p(X) = \frac{1}{n}\sum_{i=1}^n \sum_{\tilde{\mathbf{x}}} p(X|\tilde{X} = \tilde{\mathbf{x}}) q_{\mathcal{D}}(\tilde{\mathbf{x}} | \mathbf{x}_i) }[/math]
it becomes clear that the denoising autoencoder learns a semi-parametric model that can be sampled from (since [math]\displaystyle{ p(X) }[/math] above is easy to sample from).
Information Theoretic Perspective
It is also possible to adopt an information theoretic perspective. The representation of the autonencoder should retain as much information as possible while at the same time certain properties, like a limited complexity, are imposed on the marginal distribution. This can be expressed as an optimization of [math]\displaystyle{ \arg\max_{\theta} \{I(X;Y) + \lambda \mathcal{J}(Y)\} }[/math] where [math]\displaystyle{ I(X; Y) }[/math] is the mutual information between an input sample [math]\displaystyle{ X }[/math] and the hidden representation [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ \mathcal{J} }[/math] is a functional expressing the preference over the marginal. The hyper-parameter [math]\displaystyle{ \lambda }[/math] controls the trade-off between maximazing the mutual information and keeping the marginal simple.
Note that this reasoning also applies to the basic autoencoder, but the denoising autoencoder maximizes the mutual information between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] while [math]\displaystyle{ Y }[/math] can also be a function of corrupted input.
Generative Model Perspective
This section tries to recover the training criterion for denoising autoencoder. The section of 'information theoretic Perspective' is equivalent to maximizing a variational bound on a particular generative model. The final training criterion found is to maximize [math]\displaystyle{ \bold E_{q^0(\tilde{x})}[L(q^0, \tilde{X})] }[/math], where [math]\displaystyle{ L(q^0, \tilde{X}) = E_{q^0(X,Y | \tilde{X})}[log\frac{p(X, \tilde{X}, Y)}{q^0(X, Y | \tilde(X))}] }[/math]
Experiments
The Input contains different
variations of the MNIST digit classification problem, with added factors of
variation such as rotation (rot), addition of a background composed of random
pixels (bg-rand) or made from patches extracted from a set of images (bg-img), or
combinations of these factors (rot-bg-img). These variations render the problems particularly challenging for current generic learning algorithms. Each problem
is divided into a training, validation, and test set (10000, 2000, 50000 examples
respectively). A subset of the original MNIST problem is also included with the
same example set sizes (problem basic). The benchmark also contains additional
binary classification problems: discriminating between convex and non-convex
shapes (convex), and between wide and long rectangles (rect, rect-img).
Neural networks with 3 hidden layers initialized by stacking denoising autoencoders
(SdA-3), and fine tuned on the classification tasks, were evaluated
on all the problems in this benchmark. Model selection was conducted following
a similar procedure as Larochelle et al. (2007). Several values of hyper
parameters (destruction fraction ν, layer sizes, number of unsupervised training
epochs) were tried, combined with early stopping in the fine tuning phase. For
each task, the best model was selected based on its classification performance
on the validation set.
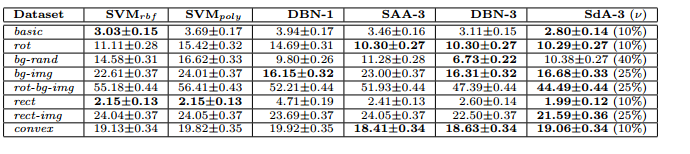
The results can be reported in the following table.
The filter obtained by training are shown the the figure below
Conclusion and Future Work
The paper shows a denoising Autoencoder which was motivated by the goal of learning representations of the input that are robust to small irrelevant changes in input. Several perspectives also help to motivate it from a manifold learning perspective and from the perspective of a generative model. This principle can be used to train and stack autoencoders to initialize a deep neural network. A series of image classification experiments were performed to evaluate this new training principle. The empirical results support the following conclusions: unsupervised initialization of layers with an explicit denoising criterion helps to capture interesting structure in the input distribution. This in turn leads to intermediate representations much better suited for subsequent learning tasks such as supervised classification. The experimental results with Deep Belief Networks (whose layers are initialized as RBMs) suggest that RBMs may also encapsulate a form of robustness in the representations they learn, possibly because of their stochastic nature, which introduces noise in the representation during training.
References
Bengio, Y. (2007). Learning deep architectures for AI (Technical Report 1312). Universit´e de Montr´eal, dept. IRO.
Bengio, Y., Lamblin, P., Popovici, D., & Larochelle, H. (2007). Greedy layerwise training of deep networks. Advances in Neural Information Processing Systems 19 (pp. 153–160). MIT Press.
Bengio, Y., & Le Cun, Y. (2007). Scaling learning algorithms towards AI. In L. Bottou, O. Chapelle, D. DeCoste and J. Weston (Eds.), Large scale kernel machines. MIT Press.
Doi, E., Balcan, D. C., & Lewicki, M. S. (2006). A theoretical analysis of robust coding over noisy overcomplete channels. In Y. Weiss, B. Sch¨olkopf and J. Platt (Eds.), Advances in neural information processing systems 18, 307–314. Cambridge, MA: MIT Press.
Doi, E., & Lewicki, M. S. (2007). A theory of retinal population coding. NIPS (pp. 353–360). MIT Press.
Elad, M., & Aharon, M. (2006). Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image Processing, 15, 3736–3745.
Gallinari, P., LeCun, Y., Thiria, S., & Fogelman-Soulie, F. (1987). Memoires associatives distribuees. Proceedings of COGNITIVA 87. Paris, La Villette
Hammond, D., & Simoncelli, E. (2007). A machine learning framework for adaptive combination of signal denoising methods. 2007 International Conference on Image Processing (pp. VI: 29–32).
Hinton, G. (1989). Connectionist learning procedures. Artificial Intelligence, 40, 185–234. Hinton, G., & Salakhutdinov, R. (2006). Reducing the dimensionality of data with neural networks. Science, 313, 504–507.
Hinton, G. E., Osindero, S., & Teh, Y. (2006). A fast learning algorithm for deep belief nets. Neural Computation, 18, 1527–1554.
Hopfield, J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences, USA, 79.
Larochelle, H., Erhan, D., Courville, A., Bergstra, J., & Bengio, Y. (2007). An empirical evaluation of deep architectures on problems with many factors of variation. Twenty-fourth International Conference on Machine Learning (ICML’2007).
LeCun, Y. (1987). Mod`eles connexionistes de l’apprentissage. Doctoral dissertation, Universit´e de Paris VI.
Lee, H., Ekanadham, C., & Ng, A. (2008). Sparse deep belief net model for visual area V2. In J. Platt, D. Koller, Y. Singer and S. Roweis (Eds.), Advances in neural information processing systems 20. Cambridge, MA: MIT Press.
McClelland, J., Rumelhart, D., & the PDP Research Group (1986). Parallel distributed processing: Explorations in the microstructure of cognition, vol. 2. Cambridge: MIT Press.
Memisevic, R. (2007). Non-linear latent factor models for revealing structure in high-dimensional data. Doctoral dissertation, Departement of Computer Science, University of Toronto, Toronto, Ontario, Canada.
Ranzato, M., Boureau, Y.-L., & LeCun, Y. (2008). Sparse feature learning for deep belief networks. In J. Platt, D. Koller, Y. Singer and S. Roweis (Eds.), Advances in neural information processing systems 20. Cambridge, MA: MIT Press.
Ranzato, M., Poultney, C., Chopra, S., & LeCun, Y. (2007). Efficient learning of sparse representations with an energy-based model. Advances in Neural Information Processing Systems (NIPS 2006). MIT Press.
Roth, S., & Black, M. (2005). Fields of experts: a framework for learning image priors. IEEE Conference on Computer Vision and Pattern Recognition (pp. 860–867).