generating text with recurrent neural networks
Introduction
The goal of this paper is to introduce a new type of recurrent neural network for character-level language modelling that allows the input character at a given timestep to multiplicatively gate the connections that make up the hidden-to-hidden layer weight matrix. The paper also introduces a solution to the problem of vanishing and exploding gradients by applying a technique called Hessian-Free optimization to effectively train a recurrent network that, when unrolled in time, has approximately 500 layers. At the date of publication, this network was arguably the deepest neural network ever trained successfully.
Strictly speaking, a language model is a probability distribution over sequences of words or characters, and they are typically used to predict the next character or word in a sequence given some number of preceding characters or words. Recurrent neural networks are naturally applicable to this problem, since they make predictions based on a current input and a hidden state whose value is determined by some number of previous inputs. Alternative methods that the authors compare their results to include a hierarchical Bayesian model called a 'sequence memoizer', and a mixture of context models referred to as PAQ, which actually includes word-level information (rather strictly character-level information). The multiplicative RNN introduced in this paper improves on the state-of-the-art for solely character-level language modelling, but is somewhat worse than the state-of-the-art for text compression.
To give a brief review, an ordinary recurrent neural network is parameterized by three weight matrices, [math]\displaystyle{ \ W_{hi} }[/math], [math]\displaystyle{ \ W_{hh} }[/math], and [math]\displaystyle{ \ W_{oh} }[/math], and functions to map a sequence of [math]\displaystyle{ N }[/math] input states [math]\displaystyle{ \ [i_1, ... , i_N] }[/math] to a sequence of hidden states [math]\displaystyle{ \ [h_1, ... , h_N] }[/math] and a sequence of output states [math]\displaystyle{ \ [o_1, ... , o_N] }[/math]. The matrix [math]\displaystyle{ \ W_{hi} }[/math] parameterizes the mapping from the current input state to the current hidden state, while the matrix [math]\displaystyle{ \ W_{hh} }[/math] parameterizes the mapping from the previous hidden state to current hidden state, such that the current hidden state is function of the previous hidden state and the current input state. Finally, the matrix [math]\displaystyle{ \ W_{oh} }[/math] parameterizes the mapping from the current hidden state to the current output state. So, at a given timestep [math]\displaystyle{ \ t }[/math], the values of the hidden state and output state are as follows:
- [math]\displaystyle{ \ h_t = tanh(W_{hi}i_t + W_{hh}h_{t-1} + b_h) }[/math]
- [math]\displaystyle{ \ o_t = W_{oh}h_t + b_o }[/math]
where [math]\displaystyle{ \ b_o }[/math] and [math]\displaystyle{ \ b_h }[/math] are bias vectors. Typically, the output state is converted into a probability distribution over characters or words using the softmax function. The network can then be treated as a generative model of text by sampling from this distribution and providing the sampled output as the input to the network at the next timestep.
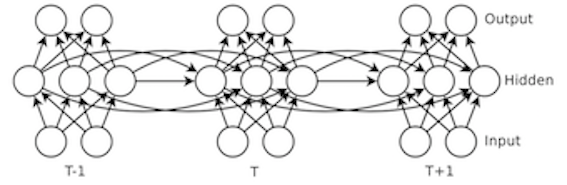
Recurrent networks are known to be very difficult to train due to the existence a highly unstable relationship between a network's parameters and the gradient of its cost function. Intuitively, the surface of the cost function is intermittently punctuated by abrupt changes (giving rise to exploding gradients) and nearly flat plateaus (giving rise to vanishing gradients) that can effectively become poor local minima when a network is trained through gradient descent. Techniques for improving training include the use of Long Short-Term Memory networks <ref> Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory." Neural computation 9.8 (1997): 1735-1780. </ref>, in which memory units are used to selectively preserve information from previous states, and the use of Echo State networks, <ref> Jaeger, H. and H. Haas. "Harnassing Nonlinearity: Predicting Chaotic Systems and Saving Energy in Wireless Communication." Science, 204.5667 (2004): 78-80. </ref> which learns only the output weights on a network with recurrent connections that implement a wide range of time-varying patterns. In this paper, the method described in the next section is used instead of these alternatives.
Hessian-Free Optimization
While this optimization technique is described elsewhere in Martens (2010), its use is essential to obtaining the successful results reported in this paper. In brief, the technique involves computing
Multiplicative Recurrent Neural Networks
The authors report that using a standard neural network trained via Hessian-free optimization produces only mediocre results. As such, they introduce a new architecture called a multiplicative recurrent neural network (MRNN). The motivating intuition behind this architecture is the idea the input at a given time step should both additively contribute to the hidden state (though the mapping performed by the input-to-hidden weights) and additionally determine the weights on the recurrent connections to the hidden state. In other words, the idea is to define a unique weight matrix [math]\displaystyle{ \ W_{hh} }[/math] for each possible input. The reason this design is hypothesized to the improve the predictive adequacy of the model is due to the idea that the conjunction of the input at one time step and the hidden state at the previous time step is important. Capturing this conjunction requires the input to influence the contribution of the previous hidden state to the current hidden state. Otherwise, the previous hidden state and the current input will make entirely independent contributions to the calculation of the current hidden state. Formally, this changes the calculation of the hidden state at a given time step as follows:
- [math]\displaystyle{ \ h_t = tanh(W_{hi}i_t + W^{i_t}_{hh}h_{t-1} + b_h) }[/math]
As a first approach to implementing this MRNN, the authors suggest using a tensor of rank 3 to store the hidden-to-hidden weights. The idea is that the tensor stores one weight matrix per possible input; when the input is provided as a one-hot vector, tensor contraction (i.e. a generalization of matrix multiplication) can be used to extract the 'slice' of the tensor that contains the appropriate set of weights. One problem with this approach is that it quickly becomes impractical to store the hidden-to-hidden weights as a tensor if the dimensionality of the hidden state has a large number of dimensions. For instance, if a network's hidden layer encodes a vector with 1000 dimensions, then the number of parameters in the tensor that need to be learned will be equal to [math]\displaystyle{ \ 1000^2 * N }[/math], where [math]\displaystyle{ \ N }[/math] is the vocabulary size. In short, this method will add many millions of parameters to a model for a non-trivially sized vocabulary.
To fix this problem, the tensor is factored using a technique described in Taylor & Hinton (2009) <ref>Taylor, G. and G. Hinton. "Factored Conditional Restricted Boltzmann Machines for Modeling Motion Style" ICML (2009) </ref>. The idea is to define three matrices [math]\displaystyle{ \ W_{fh} }[/math], [math]\displaystyle{ \ W_{fi} }[/math], and [math]\displaystyle{ \ W_{hf} }[/math] that approximate the use of a tensor in determining the value of [math]\displaystyle{ \ W^{i_t}_{hh} }[/math] as follows:
- [math]\displaystyle{ \ W^{i_t}_{hh} = W_{hf} \cdot diag(W_{fi}i_t) \cdot W_{fh} }[/math]
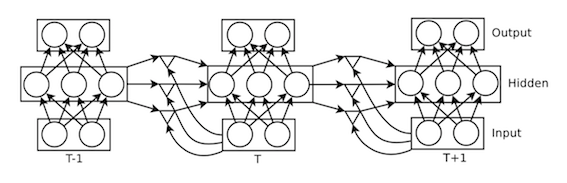
Intuitively, this factorization produces two vectors from the current input state and the previous hidden state, takes their element-wise product, and applies a linear transformation to produce the input to the hidden layer at the current timestep. The triangle units in the figure below indicate where the element-wise product occurs, and the connections into and out of these units are parameterized by the matrices [math]\displaystyle{ \ W_{fh} }[/math], [math]\displaystyle{ \ W_{fi} }[/math], and [math]\displaystyle{ \ W_{hf} }[/math]. The element-wise multiplication is implemented by diagonalizing the matrix-vector product [math]\displaystyle{ \ W_{fi}i_t }[/math], and if the dimensionality of this matrix-vector product (i.e. the dimensionality of the layer of multiplicative units) is allowed to be arbitrarily large, then this factorization is just as expressive as using a tensor to store the hidden-to-hidden weights. Note also that this factorization is what gives rise to the multiplicative gating in the network architecture.
Quantitative Experiments
Three datasets are used to train the MRNN: 100 mb of text from wikipedia, a corpus
Qualitative Experiments
Discussion
Bibliography
<references />