neural Machine Translation: Jointly Learning to Align and Translate

This summary is currently in progress.. Thank you for your patience!

Introduction

In this 2015 conference paper, Bahdanau et al. present a new way of using neural networks to perform machine translation. Rather than using the typical RNN encoder-decoder model with fixed-length intermediate vectors, the proposed method uses a joint learning process for both alignment and translation, and does not restrict intermediate encoded vectors to any specific fixed length. The result is a translation method that is comparable in performance to phrase-based systems (the state-of-the-art effective models that do not use a neural network approach), that is much more effective than other neural network models when applied to long sentences.

Previous methods

In order to better appreciate the value of this paper's contribution, it is important to understand how earlier techniques approached the problem of machine translation using neural networks.

In machine translation, the problem at hand is to identify the target sentence [math]\displaystyle{ y }[/math] (in natural language [math]\displaystyle{ B }[/math]) that is the most likely corresponding translation to the source sentence [math]\displaystyle{ x }[/math] (in natural language [math]\displaystyle{ A }[/math]). The authors compactly summarize this problem using the formula [math]\displaystyle{ \arg\min_{y} P(y|x) }[/math].

The traditional approach using neural networks, as proposed by researchers such as Kalchbrenner and Blunsom, Cho et al., Sutvesker et al., and others, is to jointly train two recursive neural networks: one that encodes the source sentence [math]\displaystyle{ x }[/math] to a vector of a fixed length, and the other that decodes this vector into a sentence in the target language.

Encoding

Typically, the encoding step iterates through the input vectors in the representation of source sentence [math]\displaystyle{ x }[/math] and updates a hidden state with each new token in the input: [math]\displaystyle{ h_t = f(x_t, h_{t-1}) }[/math], for some nonlinear function [math]\displaystyle{ f }[/math]. After the entire input is read, the resulting fixed-length representation of the entire input sentence [math]\displaystyle{ x }[/math] is given by a nonlinear function [math]\displaystyle{ q }[/math] of all of the hidden states: [math]\displaystyle{ c = q(\{h_1, \ldots, h_{T_x}\}) }[/math]. Different methods would use different nonlinear functions and different neural networks, but the essence of the approach is common to all.

Decoding

Decoding the fixed-length representation [math]\displaystyle{ c }[/math] of [math]\displaystyle{ x }[/math] is done by predicting one token of the target sentence [math]\displaystyle{ y }[/math] at a time, using the knowledge of all previously predicted words so far. The decoder defines a probability distribution over the possible sentences using a product of conditional probabilities [math]\displaystyle{ P(y) = \Pi_t P(y_t|\{y_1, \ldots, y_{t-1}\},c) }[/math].

In the neural network approach, the conditional probability of the next output term given the previous ones [math]\displaystyle{ P(y_t | \{y_1, \ldots, y_{t-1}\},c) }[/math] is given by the evaluation of a nonlinear function [math]\displaystyle{ g(y_{t-1}, s_t, c) }[/math], where [math]\displaystyle{ s_t }[/math] is the hidden state of the RNN.

The proposed method

The method proposed here is different from the traditional approach because it bypasses the fixed-length context vector [math]\displaystyle{ c }[/math] altogether, and instead aligns the tokens of the translated sentence [math]\displaystyle{ y }[/math] directly with the corresponding tokens of source sentence [math]\displaystyle{ x }[/math] as it decides which parts might be most relevant. To accommodate this, a different neural network structure needs to be set up.

Encoding

The proposed model does not use an ordinary recursive neural network to encode the target sentence [math]\displaystyle{ x }[/math], but instead uses a bidirectional recursive neural network (BiRNN): this is a model that consists of both a forward and backward RNN, where the forward RNN takes the input tokens of [math]\displaystyle{ x }[/math] in the correct order when computing hidden states, and the backward RNN takes the tokens in reverse. Thus each token of [math]\displaystyle{ x }[/math] is associated with two hidden states, corresponding to the states it produces in the two RNNs. The annotation vector [math]\displaystyle{ h_j }[/math] of the token [math]\displaystyle{ x_j }[/math] in [math]\displaystyle{ x }[/math] is given by the concatenation of these two hidden states vectors.

Aligment

An alignment model (in the form of a neural network) is used to measure how well each annotation [math]\displaystyle{ h_j }[/math] of the input sentence corresponds to the current state of constructing the translated sentence (represented by the vector [math]\displaystyle{ s_{i-1} }[/math], the hidden state of the RNN that identifies the tokens in the output sentence [math]\displaystyle{ y }[/math]. This is stored as the energy score [math]\displaystyle{ e_{ij} = a(s_{i-1}, h_j) }[/math].

The energy scores from the alignment process are used to assign weights [math]\displaystyle{ \alpha_{ij} }[/math] to the annotations, effectively trying to determine which of the words in the input is most likely to correspond to the next word that needs to be translated in the current stage of the output sequence:

[math]\displaystyle{ \alpha_{ij} = \frac{\exp(e_{ij})}{\Sigma_k \exp(e_{ik})} }[/math]

The weights are then applied to the annotations to obtain the current context vector input:

[math]\displaystyle{ c_i = \Sigma_j \alpha_{ij}h_j }[/math]

Note that this is where we see one major difference between the proposed method and the previous ones: The context vector, or the representation of the input sentence, is not one fixed-length static vector [math]\displaystyle{ c }[/math]; rather, every time we translate a new word in the sentence, a new representation vector [math]\displaystyle{ c_i }[/math] is produced. This vector depends on the most relevant words in the source sentence to the current state in the translation (hence it is automatically aligning) and allows the input sentence to have a variable length representation (since each annotation in the input representation produces a new context vector [math]\displaystyle{ c_i }[/math]).

Decoding

The decoding is done by using an RNN to model a probability distribution on the conditional probabilities

[math]\displaystyle{ P(y_i | y_1, \ldots, y_{i-1}, x) = g(y_{i-1}, s_i, c_i) }[/math]

where here, [math]\displaystyle{ s_i }[/math] is the RNN hidden state at the previous time step, and [math]\displaystyle{ c_i }[/math] is the current context vector representation as discussed above under Alignment.

Once the encoding and alignment are done, the decoding step is fairly straightforward and corresponds with the typical approach of neural network translation systems, although the context vector representation is now different at each step of the translation.

Results

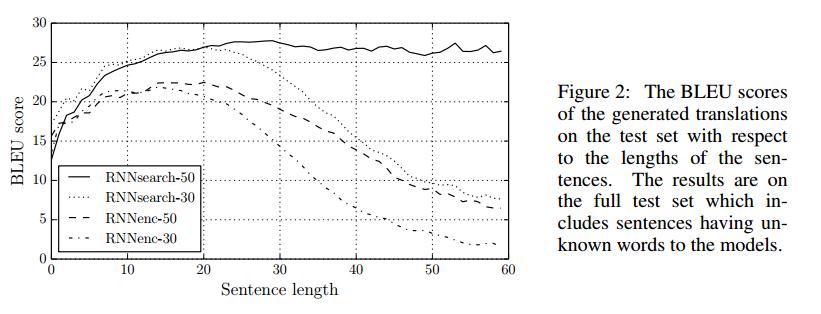
The authors performed some experiments using the proposed model of machine translation, calling it "RNNsearch", in comparison with the previous kind of model, referred to as "RNNencdec". Both models were trained on the same datasets for translating English to French, with one dataset containing sentences of length up to 30 words, and the other containing sentences with at most 50.

Quantitatively, the RNNsearch scores exceed RNNencdec by a clear margin. The distinction is particularly strong in longer sentences, which the authors note to be a problem area for RNNencdec -- information gets lost when trying to "squash" long sentences into fixed-length vector representations.

The following graph shows the performance of RNNsearch compared with RNNencdec, based on the BLEU scores for evaluating machine translation.

Qualitatively, the RNNsearch method does a good job of aligning words in the translation process, even when they need to be rearranged in the translated sentence. Long sentences are also handled very well: while RNNencdec is shown to typically lose meaning and effectiveness after a certain number of words into the sentence, RNNsearch seems robust and reliable even for unusually long sentences.

Conclusion and Comments

Overall, the algorithm proposed by the authors gives a new and seemingly useful approach towards machine translation, particularly for translating long sentences.

The performance appears to be good, but it would be interesting to see if it can be maintained when translating between languages that are not as closely aligned naturally as English and French usually are. The authors briefly refer to other languages (such as German) but do not provide any experiments or detailed comments to describe how the algorithm would perform in such cases.

It is also interesting to note that, while the performance was always shown to be better for RNNsearch than for the older RNNencdec model, the former also includes more hidden units overall in its models than the latter. RNNencdec was mentioned as having 1000 hidden units for each of its encoding and decoding RNNs, giving a total of 2000; meanwhile, RNNsearch had 1000 hidden units for each the forward and backward RNNs in encoding, as well as 1000 more for the decoding RNN, giving a total of 3000. This is perhaps a worthy point to take into consideration when judging the relative performance of the two models objectively.