stat940W25

Notes on Exercises

Exercises are numbered using a two-part system, where the first number represents the lecture number and the second number represents the exercise number. For example:

• 1.1 refers to the first exercise in Lecture 1.
• 2.3 refers to the third exercise in Lecture 2.

Students are encouraged to complete these exercises as they follow the lecture content to deepen their understanding.

Exercise 1.1

Level: ** (Moderate)

Exercise Types: Novel

Each exercise you contribute should fall into one of the following categories:

• Novel: Preferred – An original exercise created by you.
• Modified: Valued – An exercise adapted or significantly altered from an existing source.
• Copied: Permissible – An exercise reproduced exactly as it appears in the source.

References: Source: (e.g., book or other resources, if a webpage has its URL), Chapter,Page Number.

Question

Prove that the Perceptron Learning Algorithm converges in a finite number of steps if the dataset is linearly separable.

Hint:Note: exc Assume that the dataset [math]\displaystyle{ \{(\mathbf{x}_i, y_i)\}_{i=1}^N }[/math] is linearly separable, where [math]\displaystyle{ \mathbf{x}_i \in \mathbb{R}^d }[/math] are the input vectors, and [math]\displaystyle{ y_i \in \{-1, 1\} }[/math] are their corresponding labels. Show that there exists a weight vector [math]\displaystyle{ \mathbf{w}^* }[/math] and a bias [math]\displaystyle{ b^* }[/math] such that [math]\displaystyle{ y_i (\mathbf{w}^* \cdot \mathbf{x}_i + b^*) \gt 0 }[/math] for all [math]\displaystyle{ i }[/math], and use this assumption to bound the number of updates made by the algorithm.

Solution

Step 1: Linear Separability Assumption

If the dataset is linearly separable, there exists a weight vector [math]\displaystyle{ \mathbf{w}^* }[/math] and a bias [math]\displaystyle{ b^* }[/math] such that: [math]\displaystyle{ y_i (\mathbf{w}^* \cdot \mathbf{x}_i + b^*) \gt 0 \quad \forall i = 1, 2, \dots, N. }[/math] Without loss of generality, let [math]\displaystyle{ \| \mathbf{w}^* \| = 1 }[/math] (normalize [math]\displaystyle{ \mathbf{w}^* }[/math]).

Step 2: Perceptron Update Rule

The Perceptron algorithm updates the weight vector [math]\displaystyle{ \mathbf{w} }[/math] and bias [math]\displaystyle{ b }[/math] as follows:

• Initialize [math]\displaystyle{ \mathbf{w}_0 = 0 }[/math] and [math]\displaystyle{ b_0 = 0 }[/math].
• For each misclassified point [math]\displaystyle{ (\mathbf{x}_i, y_i) }[/math], update:

[math]\displaystyle{ \mathbf{w} \leftarrow \mathbf{w} + y_i \mathbf{x}_i, \quad b \leftarrow b + y_i. }[/math]

Define the margin [math]\displaystyle{ \gamma }[/math] of the dataset as: [math]\displaystyle{ \gamma = \min_{i} \frac{y_i (\mathbf{w}^* \cdot \mathbf{x}_i + b^*)}{\| \mathbf{x}_i \|}. }[/math] Since the dataset is linearly separable, [math]\displaystyle{ \gamma \gt 0 }[/math].

Step 3: Bounding the Number of Updates

Let [math]\displaystyle{ \mathbf{w}_t }[/math] be the weight vector after [math]\displaystyle{ t }[/math]-th update. Define: [math]\displaystyle{ M = \max_i \| \mathbf{x}_i \|^2, }[/math] the maximum squared norm of any input vector.

Growth of [math]\displaystyle{ \| \mathbf{w}_t \|^2 }[/math]

After [math]\displaystyle{ t }[/math] updates, the norm of [math]\displaystyle{ \mathbf{w}_t }[/math] satisfies: [math]\displaystyle{ \| \mathbf{w}_{t+1} \|^2 = \| \mathbf{w}_t + y_i \mathbf{x}_i \|^2 = \| \mathbf{w}_t \|^2 + 2 y_i (\mathbf{w}_t \cdot \mathbf{x}_i) + \| \mathbf{x}_i \|^2. }[/math] Since the point is misclassified, [math]\displaystyle{ y_i (\mathbf{w}_t \cdot \mathbf{x}_i) \lt 0 }[/math]. Thus: [math]\displaystyle{ \| \mathbf{w}_{t+1} \|^2 \leq \| \mathbf{w}_t \|^2 + \| \mathbf{x}_i \|^2 \leq \| \mathbf{w}_t \|^2 + M. }[/math] By induction, after [math]\displaystyle{ t }[/math] updates: [math]\displaystyle{ \| \mathbf{w}_t \|^2 \leq tM. }[/math]

Lower Bound on [math]\displaystyle{ \mathbf{w}_t \cdot \mathbf{w}^* }[/math]

Let [math]\displaystyle{ \mathbf{w}_t }[/math] be the weight vector after [math]\displaystyle{ t }[/math]-th update. Each update increases [math]\displaystyle{ \mathbf{w}_t \cdot \mathbf{w}^* }[/math] by at least [math]\displaystyle{ \gamma }[/math]: [math]\displaystyle{ \mathbf{w}_{t+1} \cdot \mathbf{w}^* = (\mathbf{w}_t + y_i \mathbf{x}_i) \cdot \mathbf{w}^* = \mathbf{w}_t \cdot \mathbf{w}^* + y_i (\mathbf{x}_i \cdot \mathbf{w}^*). }[/math] Since [math]\displaystyle{ y_i (\mathbf{x}_i \cdot \mathbf{w}^*) \geq \gamma }[/math], we have: [math]\displaystyle{ \mathbf{w}_{t+1} \cdot \mathbf{w}^* \geq \mathbf{w}_t \cdot \mathbf{w}^* + \gamma. }[/math] By induction: [math]\displaystyle{ \mathbf{w}_t \cdot \mathbf{w}^* \geq t \gamma. }[/math]

Combining the Results

The Cauchy-Schwarz inequality gives: [math]\displaystyle{ \mathbf{w}_t \cdot \mathbf{w}^* \leq \| \mathbf{w}_t \| \| \mathbf{w}^* \| = \| \mathbf{w}_t \|. }[/math] Thus: [math]\displaystyle{ t \gamma \leq \| \mathbf{w}_t \| \leq \sqrt{tM}. }[/math] Squaring both sides: [math]\displaystyle{ t^2 \gamma^2 \leq tM. }[/math] Dividing through by [math]\displaystyle{ t }[/math] (assuming [math]\displaystyle{ t \gt 0 }[/math]): [math]\displaystyle{ t \leq \frac{M}{\gamma^2}. }[/math]

Step 4: Conclusion

The Perceptron Learning Algorithm converges after at most [math]\displaystyle{ \frac{M}{\gamma^2} }[/math] updates, which is finite. This proves that the algorithm terminates when the dataset is linearly separable.

Exercise 1.2

Level: * (Easy)

Exercise Types: Modified

References: Simon J.D. Prince. Understanding Deep learning. 2024

This problem generalized Problem 4.10 in this textbook to [math]\displaystyle{ N }[/math] inputs and [math]\displaystyle{ M }[/math] outputs.

Question

(a) Consider a deep neural network with a single input, a single output, and [math]\displaystyle{ K }[/math] hidden layers, each containing [math]\displaystyle{ D }[/math] hidden units. How many parameters does this network have in total?

(b) Now, generalize the problem: if the number of inputs is [math]\displaystyle{ N }[/math] and the number of outputs is [math]\displaystyle{ M }[/math], how many parameters does this network have in total?

Solution

(a) Total number of parameters when there is a single input and output:

For the first layer, the input size is [math]\displaystyle{ 1 }[/math] and the output size is [math]\displaystyle{ D }[/math]. Therefore, the number of weights is [math]\displaystyle{ 1D }[/math], and the number of biases is [math]\displaystyle{ D }[/math].

Number of parameters: [math]\displaystyle{ D + D = 2D }[/math]

For hidden layers [math]\displaystyle{ i \longrightarrow i+1,i\in1,...,K-1 }[/math]: Each hidden layer connects [math]\displaystyle{ D }[/math] units to another [math]\displaystyle{ D }[/math] units. Therefore, for each layer, the number of weights is [math]\displaystyle{ D^2 }[/math], and the number of biases is [math]\displaystyle{ D }[/math].

Number of parameters for all [math]\displaystyle{ K-1 }[/math] hidden layers: [math]\displaystyle{ (K-1)(D^2 + D) }[/math]

For the output layer, the number of weights is [math]\displaystyle{ D }[/math], and the number of biases is [math]\displaystyle{ 1 }[/math].

Number of parameters: [math]\displaystyle{ D + 1 }[/math]

Therefore, the total number of parameters is [math]\displaystyle{ 2D + (K-1)(D^2 + D) + D + 1 }[/math].

(b) Total number of parameters for [math]\displaystyle{ N }[/math] inputs and [math]\displaystyle{ M }[/math] outputs:

In this case, the number of parameters for the first layer becomes [math]\displaystyle{ ND+D }[/math], while the number of parameters for the output layer becomes [math]\displaystyle{ DM+M }[/math].

Therefore, in total, the number of parameters is [math]\displaystyle{ ND+D+(K-1)(D^2+D)+MD+M }[/math]

Exercise 1.3

Level: * (Easy)

Exercise Types: Modified

References: Simon J.D. Prince. Understanding Deep learning. MIT Press, 2023

This problem modified from the background mathematics problem chap01 Question1.

Question

A single linear equation with three inputs associates a value [math]\displaystyle{ y }[/math] with each point in a 3D space [math]\displaystyle{ (x_1,x_2,x_3) }[/math]. Is it possible to visualize this? What value is at position [math]\displaystyle{ (0,0,0) }[/math]?

We add an inverse problem: If [math]\displaystyle{ y, \omega_1, \omega_2, \omega_3 }[/math] and [math]\displaystyle{ \beta }[/math] are known, derive a system of equations to solve for the input values [math]\displaystyle{ x_1, x_2, x_3 }[/math] that produce a specific output value of [math]\displaystyle{ y }[/math]. Under what conditions is this problem solvable?

Solution

A single linear equation with three inputs is of the form:

[math]\displaystyle{ y = \beta + \omega_1 x_1 + \omega_2 x_2 + \omega_3 x_3 }[/math]

where [math]\displaystyle{ \beta }[/math] is the offset, and [math]\displaystyle{ \omega_1, \omega_2, \omega_3 }[/math] are weights for the inputs [math]\displaystyle{ x_1, x_2, x_3 }[/math].

We can define the code as follows:

def linear_function_3D(x1, x2, x3, beta, omega1, omega2, omega3):
    y = beta + omega1 * x1 + omega2 * x2 + omega3 * x3
    return y

Given [math]\displaystyle{ \beta = 0.5, \omega_1 = -1.0, \omega_2 = 0.4 }[/math] and [math]\displaystyle{ \omega_3 = -0.3 }[/math],

[math]\displaystyle{ y = \beta + \omega_1 \cdot 0 + \omega_2 \cdot 0 + \omega_3 \cdot 0 }[/math]

Thus, [math]\displaystyle{ y(0, 0, 0) = 0.5. }[/math]

To visualize, we can fix [math]\displaystyle{ x_3 = 0 }[/math] and let [math]\displaystyle{ x_1, x_2 }[/math] vary, and generate the [math]\displaystyle{ y }[/math]-values using the equation.

Here is the code:

import numpy as np
import matplotlib.pyplot as plt

# Generate grid for x1 and x2, fix x3 = 0
x1 = np.linspace(-10, 10, 100)
x2 = np.linspace(-10, 10, 100)
x1, x2 = np.meshgrid(x1, x2)
x3 = 0  

# Define coefficients
beta = 0.5
omega1 = -1.0
omega2 = 0.4
omega3 = -0.3

# Compute y-values
y = linear_function_3D(x1, x2, x3, beta, omega1, omega2, omega3)

# Visualization
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x1, x2, y, cmap='viridis')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('y')
plt.title('3D Linear Function with Fixed x3=0')
plt.show()

The plot is shown below:

Visualize a single linear equation with three inputs associates a value y with each point in a 3D space.

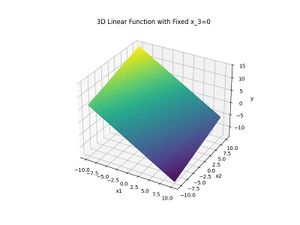
For the inverse problem, given [math]\displaystyle{ y, \beta, \omega_1, \omega_2, \omega_3, }[/math] we can solve [math]\displaystyle{ x_1, x_2, x_3 }[/math]as follows:

[math]\displaystyle{ \begin{bmatrix} \omega_1 & \omega_2 & \omega_3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = y - \beta }[/math]

The problem is solvable if [math]\displaystyle{ \omega }[/math] is not a zero vector, ensuring at least one weight contributes to the equation.

y = 10.0  
beta = 1.0
omega = [2, -1, 0.5]
rhs = y - beta

# Solve using least squares
x_vec = np.linalg.lstsq(np.array([omega]), [rhs], rcond=None)[0]
print(f"Solution for x: {x_vec}")

Exercise 1.4

Level: * (Easy)

Exercise Types: Novel

Question

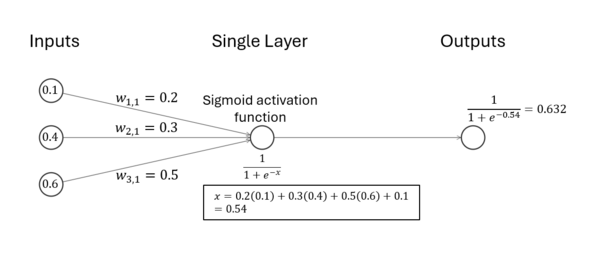
Thinking about feedforward model with sigmoid activation, compute the output of a single-layer neural network with 3 inputs and 1 output.

Assuming:

- Input vector: [math]\displaystyle{ x = (0.1, 0.4, 0.6) }[/math]

- weights: [math]\displaystyle{ w = (0.2, 0.3, 0.5) }[/math]

- Bias: [math]\displaystyle{ b = 0.1 }[/math]

- a). Sigmoid activation function: [math]\displaystyle{ f(z) = \frac{1}{1 + e^{-z}} }[/math]

- b). ReLU activation function: [math]\displaystyle{ f(z) = \max(0, z) }[/math]

- c). Tanh activation function: [math]\displaystyle{ f(z) = \tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}} }[/math]

Solution

1. Compute the weighted sum: [math]\displaystyle{ z = w \cdot x + b = (0.2)(0.1) + (0.3)(0.4) + (0.5)(0.6) + 0.1 }[/math]

Breaking this down step-by-step: [math]\displaystyle{ z = 0.02 + 0.12 + 0.3 + 0.1 = 0.54 }[/math]

2. a). Apply the sigmoid activation function: [math]\displaystyle{ f(z) = \frac{1}{1 + e^{-z}} }[/math]

Substituting [math]\displaystyle{ z = 0.54 }[/math]: [math]\displaystyle{ f(z) = \frac{1}{1 + e^{-0.54}} \approx \frac{1}{1 + 0.582} \approx 0.632 }[/math]

Thus, the final output is 0.632.

b). Similarly, apply the ReLU activation function: [math]\displaystyle{ f(z) = \max(0, z) }[/math]

Substituting [math]\displaystyle{ z = 0.54 }[/math]: [math]\displaystyle{ f(z) = \max(0, 0.54) = 0.54 }[/math]

c). Finally, apply the Tanh activation function: [math]\displaystyle{ f(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}} }[/math]

Substituting [math]\displaystyle{ z = 0.54 }[/math]: [math]\displaystyle{ f(z) = \frac{e^{0.54} - e^{-0.54}}{e^{0.54} + e^{-0.54}} \approx \frac{1.716 - 0.583}{1.716 + 0.583} \approx \frac{1.133}{2.299} \approx 0.493 }[/math]

Exercise 1.5

Level: * (Esay)

Exercise Types: Novel

Question

1.2012: ________'s ImageNet victory brings mainstream attention.

2.2016: Google's ________ uses deep learning to defeat a Go world champion.

3.2017: ________ architecture revolutionizes Natural Language Processing.

Solution

1. AlexNet

2. AlphaGo

3. Transformer

Key Milestones in Deep Learning

•2006: Deep Belief Networks – The modern era of deep learning begins.

•2012: AlexNet's ImageNet victory brings mainstream attention.

•2014-2015: Introduction of Generative Adversarial Networks (GANs).

•2016: Google's AlphaGo uses deep learning to defeat a Go world champion.

•2017: Transformer architecture revolutionizes Natural Language Processing.

•2018-2019: BERT and GPT-2 set new benchmarks in NLP.

•2020: GPT-3 demonstrates advanced language understanding and generation.

•2021: AlphaFold 2 achieves breakthroughs in protein structure prediction.

•2021-2022: Diffusion Models (e.g., DALL-E 2, Stable Diffusion) achieve state-of-the-art in image and video generation.

•2022: ChatGPT popularizes conversational AI and large language models (LLMs).

Exercise 1.6

Level: * (Easy)

Exercise Type: Novel

Question

a) What are some common examples of first-order search strategies in neural network optimization, and why are first-order methods generally preferred over second-order methods?

b) What is the difference between a deep neural network and a shallow neural network, and how many hidden layers does each typically have?

c) Prove that a perceptron cannot converge for the XOR problem.

Solution

a)

Common examples of first-order search strategies in neural network optimization include Gradient Descent (GD), Stochastic Gradient Descent (SGD), Momentum, and Adam. These methods rely on gradients (first derivatives) of the loss function to update model parameters, making them computationally efficient and scalable. First-order methods are preferred due to their efficiency, scalability to large datasets, and lower memory requirements compared to second-order methods. While second-order methods can converge faster, first-order methods like Adam balance performance and resource usage well, especially in large-scale networks.

b)

A deep neural network typically has more than 2 hidden layers, allowing it to learn complex, abstract features at each layer. A shallow neural network usually has 1 or 2 hidden layers. Therefore, networks with more than 2 hidden layers are considered deep, while those with fewer layers are considered shallow.

c)

Step 1: XOR Dataset

The XOR problem has the following data points and labels:

XOR Data

x₁	x₂	y
0	0	0
0	1	1
1	0	1
1	1	0

Step 2: Perceptron Decision Boundary

The perceptron decision boundary is defined as:

[math]\displaystyle{ z = w₁ ⋅ x₁ + w₂ ⋅ x₂ + b }[/math]

A point is classified as:

• y = 1 if z > 0
• y = 0 if z < 0

For the XOR dataset, we derive inequalities for each data point.

Step 3: Derive Inequalities

1. For (x₁, x₂) = (0, 0), y = 0:

  b < 0

2. For (x₁, x₂) = (0, 1), y = 1:

  w₂ + b > 0

3. For (x₁, x₂) = (1, 0), y = 1:

  w₁ + b > 0

4. For (x₁, x₂) = (1, 1), y = 0:

  w₁ + w₂ + b < 0

Step 4: Attempt to Solve

From the inequalities:

1. [math]\displaystyle{ b \lt 0 }[/math]

2. [math]\displaystyle{ w₂ + b \gt 0 \Rightarrow w₂ \gt -b }[/math]

3. [math]\displaystyle{ w₁ + b \gt 0 \Rightarrow w₁ \gt -b }[/math]

4. [math]\displaystyle{ w₁ + w₂ + b \lt 0 \Rightarrow w₁ + w₂ \lt -b }[/math]

Now, add inequalities (2) and (3):

[math]\displaystyle{ w₁ + w₂ \gt -2b }[/math]

But compare this with inequality (4):

[math]\displaystyle{ w₁ + w₂ \lt -b }[/math]

This leads to a contradiction because [math]\displaystyle{ -2b \lt -b }[/math] cannot be true if [math]\displaystyle{ b \lt 0 }[/math].

Therefore, the XOR dataset is not linearly separable, and the perceptron cannot converge for the XOR problem.

Exercise 1.7

Level: * (Easy)

Exercise Type: Novel

Question

The sigmoid activation function is defined as: [math]\displaystyle{ \sigma(x) = \frac{1}{1 + e^{-x}}. }[/math]

(a) Derive the derivative of [math]\displaystyle{ \sigma(x) }[/math] with respect to [math]\displaystyle{ x }[/math], and show that: [math]\displaystyle{ \sigma'(x) = \sigma(x)(1 - \sigma(x)). }[/math]

(b) Use this property to explain why sigmoid activation is suitable for modeling probabilities in binary classification tasks.

Solution

(a) Derivative: Starting with [math]\displaystyle{ \sigma(x) = \frac{1}{1 + e^{-x}} }[/math]: [math]\displaystyle{ \sigma'(x) = \frac{d}{dx} \left( \frac{1}{1 + e^{-x}} \right) = \frac{e^{-x}}{(1 + e^{-x})^2}. }[/math] Simplifying using [math]\displaystyle{ \sigma(x) = \frac{1}{1 + e^{-x}} }[/math] and [math]\displaystyle{ 1 - \sigma(x) = \frac{e^{-x}}{1 + e^{-x}} }[/math], we find: [math]\displaystyle{ \sigma'(x) = \sigma(x)(1 - \sigma(x)). }[/math]

(b) The sigmoid function outputs values in the range [math]\displaystyle{ (0, 1) }[/math], making it ideal for modeling probabilities. The derivative [math]\displaystyle{ \sigma'(x) = \sigma(x)(1 - \sigma(x)) }[/math] ensures that gradient updates during optimization are proportional to the confidence of the prediction, preventing drastic updates for very confident predictions. Here, we want to mention that softmax function is also suitable for binary classification problem.

Exercise 1.8

Level: * (Easy)

Exercise Types: Novel

Question

In classification, it is possible to minimize the number of misclassifications directly by using:

[math]\displaystyle{ \sum_{i=1}^n \mathbf{1}\Bigl(\text{sign}(\boldsymbol{\beta}^T \mathbf{x}_i + \beta_0) \neq y_i\Bigr) }[/math]

where [math]\displaystyle{ \mathbf{1}(\cdot) }[/math] is the indicator function, [math]\displaystyle{ \boldsymbol{\beta} }[/math] is the weight vector, and [math]\displaystyle{ \beta_0 }[/math] is the bias term. So, the loss function gives 1 for each incorrect response and 0 for each correct one.

(a) Why is this approach not commonly used in practice?

(b) Name and give formulas for two differentiable loss functions commonly employed in practice for binary classification tasks, explaining why they are more popular.

Solution

(a): The expression [math]\displaystyle{ \mathbf{1}\left(\text{sign}(\boldsymbol{\beta}^T \mathbf{x}_i + \beta_0) \neq y_i \right) }[/math] gives only 0 or 1. Small changes in [math]\displaystyle{ \boldsymbol{\beta} }[/math] or [math]\displaystyle{ \beta_0 }[/math] can suddenly change the loss function for a sample from 0 to 1 (or vice versa). Because the loss function is discrete, the gradient with respect to [math]\displaystyle{ \boldsymbol{\beta} }[/math] or [math]\displaystyle{ \beta_0 }[/math] does not exist. Standard optimization techniques like gradient descent rely on differentiable, continuous loss function where partial derivatives can use to update the parameters.

(b): Two alternative loss functions:

Hinge Loss: [math]\displaystyle{ \sum_{i=1}^n \max(0, 1 - y_i (\boldsymbol{\beta}^T \mathbf{x}_i + \beta_0)) }[/math]

The hinge loss is often used in Support Vector Machines (SVMs) and works well when the data is linearly separable.

Logistic (Cross-Entropy) Loss: [math]\displaystyle{ \sum_{i=1}^n \log\left( 1 + \exp(-y_i (\boldsymbol{\beta}^T \mathbf{x}_i + \beta_0)) \right) }[/math]

The logistic loss (or cross-entropy loss) is commonly used in logistic regression and neural networks. It is differentiable so it works well for gradient-based optimization methods.

Exercise 1.9

Level: ** (Easy)

Exercise Types: Novel

Question

How are neural networks modeled?

Solution

Neural networks are modeled from biological neurons. A neural network consists of layers of interconnected neurons where each connection has associated weights. The input layer receives the data features, and each neuron corresponds to one feature from the dataset. The hidden layer consists of multiple neurons that transform the input data into intermediate representations, using a combination of weights, biases, and activation functions which allows the network to learn complex patterns, like the Sigmoid function [math]\displaystyle{ S(x) = \frac {1}{1+e^{-x}} }[/math]. The output layer generates the final prediction, such as probabilities for classification or continuous values for regression. Neural networks learn to map inputs to outputs by adjusting weights during training to minimize the error between predicted and actual outputs.

For example, in the lecture note, inputs [math]\displaystyle{ x_1 = 0.5 , x_2 = 0.9, x_3 = -0.3 }[/math] are passed through a hidden layer with specific weights:

[math]\displaystyle{ H_1 ~ weight = (1.0,-2.0,2.0) }[/math],

[math]\displaystyle{ H_2 ~ weight= (2.0,1.0 -4.0) }[/math],

[math]\displaystyle{ H_3 ~ weight = (1.0,-1.0,0.0) }[/math].

The computations yield hidden neuron values of

[math]\displaystyle{ H_1 = 0.5\times1.0 + 0.9\times -2.0 + -0.3 \times 2.0= 0.13 }[/math],

[math]\displaystyle{ H_2 = 0.5\times 2.0 + 0.9\times 1.0 + -0.3\times -4.0= 0.96 }[/math],

[math]\displaystyle{ H_3 = 0.5\times 1.0 + 0.9\times -1.0+ -0.3\times 0.0 = 0.40 }[/math],

which are then processed by the output layer to produce predictions.

Exercise 1.10

Level: ** (Moderate)

Exercise Types: Novel

Question

Biological neurons in the human brain have the following characteristics:

1. A neuron fires an electrical signal only when its membrane potential exceeds a certain threshold. Otherwise, it remains inactive.

2. Neurons are connected to one another through dendrites (input) and axons (outputs), forming a highly interconnected network.

3. The intensity of the signal passed between neurons depends on the strength of the connection, which can change over time due to learning and adaptation.

Considering the above points, answer the following questions:

Explain how these biological properties of neurons might inspire the design and functionality of nodes in artificial neural networks.

Solution

1. Threshold Behavior: The concept of a neuron firing only when its membrane potential exceeds a threshold is mirrored in neural networks through activation functions. These functions decide whether a node "fires" by producing a significant output.

2. Connectivity: The connections between biological neurons via dendrites and axons inspire the weighted connections in artificial neural networks. Each node receives inputs, processes them, and sends weighted outputs to subsequent node, similar how to signals propagate in the brain.

3. Learning and Adaptation: Biological neurons strengthen or weaken their connections based on experience (neuroplasticity). This is similar to how artificial networks adjust weights during training using backpropagation and optimization algorithms. The dynamic modification of weights allows artificial networks to learn from data.

Exercise 1.11

Level: * (Easy)

Exercise Type: Novel

Question

If the pre-activation is 20, what are the outputs of the following activation functions: ReLU, Leaky ReLU, logistic, and hyperbolic?

Choose the correct answer:
a) 20, 20, 1, 1
b) 20, 0, 1, 1
c) 20, -20, 1, 1
d) 20, 20, -1, 1
e) 20, -20, 1, -1

Solution

The correct answer is a): 20, 20, 1, 1.

Calculation

[math]\displaystyle{ \text{ReLU}(20) = \max(0, 20) = 20 }[/math]

[math]\displaystyle{ \text{LeakyReLU}(20) = \begin{cases} 20 & \text{if } 20 \geq 0 \\ \alpha \cdot 20 & \text{if } 20 \lt 0 \end{cases} = 20 }[/math] where [math]\displaystyle{ \alpha }[/math] is a small constant (typically [math]\displaystyle{ 0.01 }[/math]).

[math]\displaystyle{ \sigma(20) = \frac{1}{1 + e^{-20}} \approx 1 }[/math]

[math]\displaystyle{ \tanh(20) = \frac{e^{20} - e^{-20}}{e^{20} + e^{-20}} = 1 }[/math]

Exercise 1.12

Level: * (Easy)

Exercise Type: Novel

Question

Imagine a simple feedforward neural network with a single hidden layer. The network structure is as follows: - linear activation function - The input layer has 2 neurons. - The hidden layer has 2 neurons. - The output layer has 1 neuron. - There are no biases in the network.

If the weights from the input layer to the hidden layer are given by: [math]\displaystyle{ W^{(1)} = \begin{bmatrix} 0.5 & -0.6 \\ 0.1 & 0.8 \end{bmatrix} }[/math] and the weights from the hidden layer to the output layer are given by: [math]\displaystyle{ W^{(2)} = \begin{bmatrix} 0.3 \\ -0.2 \end{bmatrix} }[/math]

Calculate the output of the network for the input vector [math]\displaystyle{ \mathbf{x} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} }[/math] using a linear activation function for all neurons.

Hint

- The output of each layer is calculated by multiplying the input of that layer by the layer's weight matrix. - Use matrix multiplication to compute the outputs step-by-step.

Solution

• • Step 1: Calculate Hidden Layer Output**

The input to the hidden layer is the initial input [math]\displaystyle{ \mathbf{x} }[/math]: [math]\displaystyle{ h^{(1)} = W^{(1)} \times \mathbf{x} = \begin{bmatrix} 0.5 & -0.6 \\ 0.1 & 0.8 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0.5 \\ 0.1 \end{bmatrix} }[/math]

• • Step 2: Calculate Output Layer Output**

The input to the output layer is the output from the hidden layer: [math]\displaystyle{ y = W^{(2)} \times h^{(1)} = \begin{bmatrix} 0.3 \\ -0.2 \end{bmatrix} \times \begin{bmatrix} 0.5 \\ 0.1 \end{bmatrix} = 0.3 \times 0.5 + (-0.2) \times 0.1 = 0.15 - 0.02 = 0.13 }[/math]

Thus, the output of the network for the input vector [math]\displaystyle{ \mathbf{x} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} }[/math] is [math]\displaystyle{ 0.13 }[/math].

Exercise 1.13

Level: * (Easy)

Exercise Types: Novel

Question

Explain whether this is a classification, regression, or clustering task each time. If the task is either classification or regression, also comment on whether the focus is prediction or explanation.

1. **Stock Market Trends:**

  A financial analyst wants to predict the future stock prices of a company based on historical trends, economic indicators, and company performance metrics.

2. **Customer Segmentation:**

  A retail company wants to group its customers based on their purchasing behaviour, including transaction frequency, product categories, and total spending, to design targeted marketing campaigns.

3. **Medical Diagnosis:**

  A hospital wants to develop a model to determine whether a patient has a specific disease based on symptoms, medical history, and lab test results.

4. **Predicting Car Fuel Efficiency:**

  An automotive researcher wants to understand how engine size, weight, and aerodynamics affect a car's fuel efficiency (miles per gallon).

Solution

**1. Stock Market Trends**

• • Task Type:** Regression
  • Focus:** Prediction
  • Reasoning:** Stock prices are continuous numerical values, making this a regression task. The goal is to predict future prices rather than explain past fluctuations.

**2. Customer Segmentation**

• • Task Type:** Clustering
  • Focus:** —
  • Reasoning:** Customers are grouped based on their purchasing behaviour without predefined labels, making this a clustering task.

**3. Medical Diagnosis**

• • Task Type:** Classification
  • Focus:** Prediction
  • Reasoning:** The disease status is a categorical outcome (Has disease: Yes/No), making this a classification problem. The goal is to predict a diagnosis for future patients.

**4. Predicting Car Fuel Efficiency**

• • Task Type:** Regression
  • Focus:** Explanation
  • Reasoning:** Fuel efficiency (miles per gallon) is a continuous variable. The researcher is interested in understanding how different factors influence efficiency, so the focus is on explanation.

Summary

Task	Type	Focus	Reasoning
Stock Market Trends	Regression	Prediction	Predict future stock prices (continuous variable).
Customer Segmentation	Clustering	—	Group customers based on purchasing behaviour.
Medical Diagnosis	Classification	Prediction	Determine if a patient has a disease (Yes/No).
Predicting Car Fuel Efficiency	Regression	Explanation	Understand how factors affect fuel efficiency.

Exercise 1.14

Level: ** (Easy)

Exercise Types: Novel

Question

You are given a set of real-world scenarios. Your task is to identify the most suitable fundamental machine learning approach for each scenario and justify your choice.

• • Scenarios:**

1. **Loan Default Prediction:**

  A bank wants to predict whether a loan applicant will default on their loan based on their credit history, income, and employment status.

2. **House Price Estimation:**

  A real estate company wants to estimate the price of a house based on features such as location, size, and number of bedrooms.

3. **User Grouping for Advertising:**

  A social media platform wants to group users with similar interests and online behavior for targeted advertising.

4. **Dimensionality Reduction in Medical Data:**

  A medical researcher wants to reduce the number of variables in a dataset containing hundreds of patient health indicators while retaining the most important information.

• • Tasks:**

- For each scenario, classify the problem into one of the four fundamental categories: Classification, Regression, Clustering, or Dimensionality Reduction. - Explain why you selected that category for each scenario. - Suggest a possible algorithm that could be used to solve each problem.

Solution

• • 1. Loan Default Prediction**
  • Task Type:** Classification
  • Reasoning:** The target variable (loan default) is categorical (Yes/No), making this a classification problem. The goal is to predict whether an applicant will default based on their financial history.
  • Possible Algorithm:** Logistic Regression, Random Forest, or Gradient Boosting.

• • 2. House Price Estimation**
  • Task Type:** Regression
  • Reasoning:** House prices are continuous numerical values, making this a regression task. The goal is to estimate a house's price based on features like location and size.
  • Possible Algorithm:** Linear Regression, Decision Trees, or XGBoost.

• • 3. User Grouping for Advertising**
  • Task Type:** Clustering
  • Reasoning:** The goal is to group users based on their behavior without predefined labels, making this a clustering task.
  • Possible Algorithm:** K-Means, DBSCAN, or Hierarchical Clustering.

• • 4. Dimensionality Reduction in Medical Data**
  • Task Type:** Dimensionality Reduction
  • Reasoning:** The goal is to reduce the number of variables while preserving essential information, making this a dimensionality reduction task.
  • Possible Algorithm:** Principal Component Analysis (PCA), t-SNE, or Autoencoders.

Exercise 1.15

Level: ** (Easy)

Exercise Types: Novel

Question

Define what machine learning is and how it is different from classical statistics. Provide the three learning methods used in machine learning, briefly define each and give an example of where each of them can be used. Include some common algorithms for each of the learning methods.

Solution

• • Machine learning Definition**

– Machine Learning is the ability to teach a computer without explicitly programming it

– Examples are used to train computers to perform tasks that would be difficult to program

The difference between classical statistics and machine learning is the size of the data that they infer information from. In classical statistics, this is usually done from a small dataset(not enough data) while in machine learning it is done from a large dataset(Too many data).

• • Supervised learning**

Supervised learning is a type of machine learning where the model is trained on a labeled dataset, meaning each training example has input features and a corresponding correct output. The algorithm learns the relationship between inputs and outputs to make predictions on new, unseen data.

Examples: Predicting house prices based on location, size, and other features (Regression). Identifying whether an email is spam or not (Classification).

Common Algorithms: Linear Regression, Logistic Regression, Decision Trees, Random Forest, Support Vector Machines (SVM), Neural Networks.

• • Unsupervised Learning**

Unsupervised learning involves training a model on data without labeled outputs. The algorithm attempts to discover patterns, structures, or relationships within the data.

Examples: Grouping customers with similar purchasing behaviors for targeted marketing (Clustering). Identifying important features in a high-dimensional dataset (Dimensionality Reduction).

Common Algorithms: K-Means, Hierarchical Clustering, DBSCAN (Clustering). Principal Component Analysis (PCA), t-SNE, Autoencoders (Dimensionality Reduction).

• • Reinforcement Learning**

Reinforcement learning (RL) is a type of machine learning where an agent learns to make decisions by performing actions in an environment to maximize cumulative rewards. The agent interacts with the environment, receives feedback in the form of rewards or penalties, and improves its strategy over time.

Examples: Training a robot to walk by rewarding successful movements. Teaching an AI to play chess or video games by rewarding wins and penalizing losses.

Common Algorithms: Q-Learning, Deep Q Networks (DQN), Policy Gradient Methods, Proximal Policy Optimization (PPO).

Summary

Aspect	Supervised Learning	Unsupervised Learning	Reinforcement Learning
Definition	Learning from labeled data where inputs are paired with outputs.	Learning patterns or structures from unlabeled data.	Learning by interacting with an environment to maximize cumulative rewards.
Key Characteristics	Trains on known inputs and outputs to predict outcomes for unseen data.	No predefined labels; discovers hidden structures in the data.	Agent learns through trial and error by receiving rewards or penalties for its actions.
Examples	- Predicting house prices (Regression). - Classifying emails as spam or not (Classification).	- Grouping customers by behavior (Clustering). - Reducing variables in large datasets (Dimensionality Reduction).	- Training robots to walk. - Teaching AI to play chess or video games.
Common Algorithms	- Linear Regression - Logistic Regression - Decision Trees - Random Forest - SVM - Neural Networks	- K-Means - Hierarchical Clustering - PCA - t-SNE - Autoencoders	- Q-Learning - Deep Q Networks (DQN) - Policy Gradient Methods - Proximal Policy Optimization (PPO)

Exercise 1.16

Level: * (Easy)

Exercise Types: Novel

Question

Categorize each of these machine learning scenarios into supervised learning, unsupervised learning, or reinforcement learning. Justify your reasoning for each case.

(a) A neural network is trained to classify handwritten digits using the MNIST dataset, which contains 60 000 images of handwritten digits, along with the correct answer for each image.

(b) A robot is programmed to learn how to play a video game. It does not have access to the game’s rules, but it can observe its current score after each action. Over time, it learns to play better by maximizing its score.

(c) A deep learning model is designed to segment medical images into different sections corresponding to specific organs. The training data consists of medical scans that have been annotated by experts to mark the boundaries of the organs.

(d) A machine learning model is given 100 000 astronomical images of unknown stars and galaxies. Using dimensionality reduction techniques, it groups similar-looking objects based on their features, such as size and shape.

Solution

(a) Supervised learning: The model is trained with labeled data, where each image has a corresponding digit label.

(b) Reinforcement learning: The model learns by interacting with an environment and receiving feedback in the form of rewards or penalties. It explores different actions to maximize cumulative rewards over time.

(c) Supervised learning: The model uses labeled data where professionals annotated each region of the image.

(d) Unsupervised learning: The model works with unlabeled data to find patterns and group similar objects.

Exercise 1.17

Level: * (Easy)

Exercise Types: Novel

Question

How does the introduction of ReLU as an activation function address the vanishing gradient problem observed in early deep learning models using sigmoid or tanh functions?

Solution

The vanishing gradient problem occurs when activation functions like sigmoid or tanh compress their inputs into small ranges, resulting in gradients that become very small during backpropagation. This hinders learning, particularly in deeper networks.

The ReLU (Rectified Linear Unit), defined as [math]\displaystyle{ f(x) = \max(0, x) }[/math], addresses this issue effectively:

(a) Non-Saturating Gradients: For positive input values, ReLU's gradient remains constant (equal to 1), preventing gradients from vanishing.

(b) Efficient Computation: The simplicity of the ReLU function makes it computationally faster than the sigmoid or tanh functions, which involve more complex exponential calculations.

(c) Sparse Activations: ReLU outputs zero for negative inputs, leading to sparse activations, which can improve computational efficiency and reduce overfitting.

However, ReLU can experience the "dying ReLU" problem, where neurons output zero for all inputs and effectively become inactive. Variants like Leaky ReLU and Parametric ReLU address this by allowing small, non-zero gradients for negative inputs, ensuring neurons remain active.

Exercise 2.1

Level: * (Easy)

Exercise Types: Novel

References: Calin, Ovidiu. Deep learning architectures: A mathematical approach. Springer, 2020

This problem is coincidentally similar to Exercise 5.10.1 (page 163) in this textbook, although that exercise was not used as the basis for this question.

Question

This problem is about using perceptrons to implement logic functions. Assume a dataset of the form [math]\displaystyle{ x_1, x_2 \in \{0, 1\} }[/math], and a perceptron defined as: [math]\displaystyle{ y = H(\beta_0 + \beta_1 x_1 + \beta_2 x_2), }[/math] where [math]\displaystyle{ H }[/math] is the Heaviside step function, defined as: [math]\displaystyle{ H(z) = \begin{cases} 1, & \text{if } z \geq 0, \\ 0, & \text{if } z \lt 0. \end{cases} }[/math]

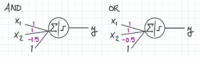
(a)* Find weights [math]\displaystyle{ \beta_1, \beta_2 }[/math] and bias [math]\displaystyle{ \beta_0 }[/math] for a single perceptron that implements the AND function.

(b)* Find the weights [math]\displaystyle{ \beta_1, \beta_2 }[/math] and bias [math]\displaystyle{ \beta_0 }[/math] for a single perceptron that implements the OR function.

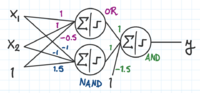
(c)** Given the truth table for the XOR function:

[math]\displaystyle{ \begin{array}{|c|c|c|} \hline x_1 & x_2 & x_1 \oplus x_2 \\ \hline 0 & 0 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\ \hline \end{array} }[/math]

Show that it cannot be learned by a single perceptron. Find a small neural network of multiple perceptrons that can implement the XOR function. (Hint: a hidden layer with 2 perceptrons).

Solution

(a) A perceptron that implements the AND function:

[math]\displaystyle{ y = H(-1.5 + x_1 + x_2). }[/math]

Here:

[math]\displaystyle{ \beta_0 = -1.5, \quad \beta_1 = 1, \quad \beta_2 = 1. }[/math]. This works because the AND function returns 1 only when both inputs are 1. For a perceptron, the condition for activation is: [math]\displaystyle{ \beta_0 + \beta_1 x_1 + \beta_2 x_2 \geq 0. }[/math] This must hold for (1, 1) but fail for all other combinations. Substituting values leads to the choice of [math]\displaystyle{ \beta_0 = -1.5 }[/math] and [math]\displaystyle{ \beta_1 = \beta_2 = 1 }[/math].

(b) A perceptron that implements the OR function:

[math]\displaystyle{ y = H(-0.5 + x_1 + x_2). }[/math]

Here:

[math]\displaystyle{ \beta_0 = -0.5, \quad \beta_1 = 1, \quad \beta_2 = 1. }[/math] This works because the OR function returns 1 if either or both inputs are 1. Using similar logic to the AND case, the decision boundary conditions lead to these parameters.

Perceptrons that implement the AND and OR functions respectively.

(c) XOR is not linearly separable, so it cannot be implemented by a single perceptron.

The XOR function returns 1 when the following are true:

• Either [math]\displaystyle{ x_1 }[/math] or [math]\displaystyle{ x_2 }[/math] are 1. In other words, the expression [math]\displaystyle{ x_1 }[/math] OR [math]\displaystyle{ x_2 }[/math] returns 1.
• [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math] are not both 1. In other words, the expression [math]\displaystyle{ x_1 }[/math] NAND [math]\displaystyle{ x_2 }[/math] returns 1.

To implement this, the outputs of an OR and a NAND perceptron can be taken as inputs to an AND perceptron. (The NAND perceptron was derived by multiplying the weights and bias of the AND perceptron by -1.)

Neural network that implements the XOR function.

Why can't the perceptron converge in the case of linear non-separability?

In linearly separable data, there exists a weight vector [math]\displaystyle{ w }[/math] and bias [math]\displaystyle{ b }[/math] such that:

[math]\displaystyle{ y_i(w \cdot x_i + b) \gt 0 \quad \forall i }[/math]

But in the case of linear non-separability, w and b satisfying this condition do not exist, so the perceptron cannot satisfy the convergence condition.

Exercise 2.2

Level: * (Easy)

Exercise Types: Novel

Question

1.How do feedforward neural networks utilize backpropagation to adjust weights and improve the accuracy of predictions during training?

2. How would the training process be affected if the learning rate in optimization algorithm were too high or too low?

Solution

1. After a forward pass where inputs are processes to generate an output, the error between the prediction and actual values is calculated. This error is then propagated backward through the network, and the gradients of the loss function with respect to the weights are computed. Using these gradients, the weights are updated with an optimization algorithm like stochastic gradient descent, gradually minimizing the error and improving the networks' performance.

2. If the learning rate is too high, the weights might overshoot the optimal values, leading to oscillations or divergence. If it's too low, the training process might become very slow and stuck in local minimum.

Calculations

Step 1: Forward Propagation

Each neuron computes:

[math]\displaystyle{ z = W \cdot x + b }[/math]

[math]\displaystyle{ a = f(z) }[/math]

where:

• W = weights, b = bias
• f(z) = activation function (e.g., sigmoid, ReLU)
• a = neuron’s output

Step 2: Compute Loss

The error between predicted [math]\displaystyle{ \hat{y} }[/math] and actual [math]\displaystyle{ y }[/math] is calculated using a loss function, such as **Mean Squared Error (MSE)**:

[math]\displaystyle{ L = \frac{1}{n} \sum (y - \hat{y})^2 }[/math]

For classification, **Cross-Entropy Loss** is commonly used.

Step 3: Backward Propagation

Using the **chain rule**, gradients are computed:

[math]\displaystyle{ \frac{\partial L}{\partial W} = \frac{\partial L}{\partial a} \cdot \frac{\partial a}{\partial z} \cdot \frac{\partial z}{\partial W} }[/math]

These gradients guide weight updates to minimize loss.

Step 4: Weight Update using Gradient Descent

Weights are updated using:

[math]\displaystyle{ W = W - \alpha \frac{\partial L}{\partial W} }[/math]

where [math]\displaystyle{ \alpha }[/math] is the **learning rate**.

Exercise 2.3

Level: * (Easy)

Exercise Types: Modified

References: Simon J.D. Prince. Understanding Deep learning. 2024

This problem comes from Problem 3.5 in this textbook. In addition to the proof, I explained why this property is important to learning neural networks.

Question

Prove that the following property holds for [math]\displaystyle{ \alpha \in \mathbb{R}^+ }[/math]:

[math]\displaystyle{ \text{ReLU}[\alpha \cdot z] = \alpha \cdot \text{ReLU}[z] }[/math]

Explain why this property is important in neural networks.

Solution

This is known as the non-negative homogeneity property of the ReLU function.

Recall the definition of the ReLU function:

[math]\displaystyle{ \text{ReLU}(z) = \begin{cases} z & \text{if } z \geq 0, \\ 0 & \text{if } z \lt 0. \end{cases} }[/math]

We prove the property by considering the two possible cases for [math]\displaystyle{ z }[/math].

Case 1: [math]\displaystyle{ z \geq 0 }[/math]

If [math]\displaystyle{ z \geq 0 }[/math], then by the definition of the ReLU function:

[math]\displaystyle{ \text{ReLU}(z) = z }[/math]

Therefore:

[math]\displaystyle{ \text{ReLU}(\alpha \cdot z) = \alpha \cdot z }[/math]

and:

[math]\displaystyle{ \alpha \cdot \text{ReLU}(z) = \alpha \cdot z }[/math]

Hence, in this case:

[math]\displaystyle{ \text{ReLU}(\alpha \cdot z) = \alpha \cdot \text{ReLU}(z) }[/math]

Case 2: [math]\displaystyle{ z\lt 0 }[/math]

If [math]\displaystyle{ z \lt 0 }[/math], then [math]\displaystyle{ \alpha \cdot z \lt 0 }[/math].

Therefore:

[math]\displaystyle{ \text{ReLU}(\alpha \cdot z) = \text{ReLU}(z) = 0 }[/math]

and:

[math]\displaystyle{ \alpha \cdot \text{ReLU}(z) = \alpha \cdot 0 = 0 }[/math]

Hence, in this case:

[math]\displaystyle{ \text{ReLU}(\alpha \cdot z) = \alpha \cdot \text{ReLU}(z) }[/math]

Since the property holds in both cases, this completes the proof.

Why is this property important in neural networks?

In a neural network, the input to a neuron is often a linear combination of the weights and inputs.

When training neural networks, scaling the inputs or weights can affect the activations of neurons. However, because ReLU satisfies the homogeneity property, the output of the ReLU function scales proportionally with the input. This means that scaling the inputs by a positive constant (like a learning rate or normalization factor) does not change the overall pattern of activations — it only scales them. This stability in scaling is important during optimization because it makes the network's output more predictable and ensures that scaling transformations don't break the network's functionality.

Additionally, because of the non-negative homogeneity property, the gradients also scale proportionally, the scale of the gradient changes proportionally with the input scale, which ensures that the optimization process remains stable. It helps prevent exploding gradients when the inputs are scaled by large positive values.

The homogeneity property of ReLU also helps the network to perform well on different types of data. By keeping the scaling of activations consistent, it helps maintain the connection between inputs and outputs during training, even when the data is adjusted or scaled. This makes ReLU useful when input values vary a lot, and it simplifies the network's response to changes in input distributions, which is especially valuable when transferring a trained model to new data or domains.

Exercise 2.4

Level: * (Easy)

Exercise Types: Novel

Question

Train a perceptron on the given dataset using the following initial settings, and ensure it classifies all data points correctly.

• Initial weights: [math]\displaystyle{ w_0 = 0, w_1 = 0, w_2 = 0 }[/math]
• Learning rate: [math]\displaystyle{ \eta = 0.1 }[/math]
• Training dataset:

  (x₁ = 1, x₂ = 2, y = 1)
  (x₁ = -1, x₂ = -1, y = -1)
  (x₁ = 2, x₂ = 1, y = 1)

[math]\displaystyle{ y = 1 }[/math] if the output [math]\displaystyle{ z = w_1 \cdot x_1 + w_2 \cdot x_2 + w_0 \geq 0 }[/math], otherwise [math]\displaystyle{ y = -1 }[/math].

Solution

Iteration 1

1. First data point (x₁ = 1, x₂ = 2) with label 1:

• Weighted sum: [math]\displaystyle{ \hat{y} = w_0 + w_1 x_1 + w_2 x_2 = 0 + 0(1) + 0(2) = 0 }[/math]
• Predicted label: [math]\displaystyle{ \hat{y} = 1 }[/math]
• Actual label: 1 → No misclassification

2. Second data point (x₁ = -1, x₂ = -1) with label -1:

• Weighted sum: [math]\displaystyle{ \hat{y} = w_0 + w_1 x_1 + w_2 x_2 = 0 + 0(-1) + 0(-1) = 0 }[/math]
• Predicted label: [math]\displaystyle{ \hat{y} = 1 }[/math]
• Actual label: -1 → Misclassified

3. Third data point (x₁ = 2, x₂ = 1) with label 1:

• Weighted sum: [math]\displaystyle{ \hat{y} = w_0 + w_1 x_1 + w_2 x_2 = 0 + 0(2) + 0(1) = 0 }[/math]
• Predicted label: [math]\displaystyle{ \hat{y} = 1 }[/math]
• Actual label: 1 → No misclassification

Update Weights (using the Perceptron rule with the cost as the distance of all misclassified points)

For the misclassified point (x₁ = -1, x₂ = -1):

• Updated weights:
• [math]\displaystyle{ w_0 = w_0 + \eta y = 0 + 0.1(-1) = -0.1 }[/math]
• [math]\displaystyle{ w_1 = w_1 + \eta y x_1 = 0 + 0.1(-1)(-1) = 0.1 }[/math]
• [math]\displaystyle{ w_2 = w_2 + \eta y x_2 = 0 + 0.1(-1)(-1) = 0.1 }[/math]

Updated weights after first iteration: [math]\displaystyle{ w_0 = -0.1, w_1 = 0.1, w_2 = 0.1 }[/math]

Iteration 2

1. First data point (x₁ = 1, x₂ = 2) with label 1:

• Weighted sum: [math]\displaystyle{ \hat{y} = -0.1 + 0.1(1) + 0.1(2) = -0.1 + 0.1 + 0.2 = 0.2 }[/math]
• Predicted label: [math]\displaystyle{ \hat{y} = 1 }[/math]
• Actual label: 1 → No misclassification

2. Second data point (x₁ = -1, x₂ = -1) with label -1:

• Weighted sum: [math]\displaystyle{ \hat{y} = -0.1 + 0.1(-1) + 0.1(-1) = -0.1 - 0.1 - 0.1 = -0.3 }[/math]
• Predicted label: [math]\displaystyle{ \hat{y} = -1 }[/math]
• Actual label: -1 → No misclassification

3. Third data point (x₁ = 2, x₂ = 1) with label 1:

• Weighted sum: [math]\displaystyle{ \hat{y} = -0.1 + 0.1(2) + 0.1(1) = -0.1 + 0.2 + 0.1 = 0.2 }[/math]
• Predicted label: [math]\displaystyle{ \hat{y} = 1 }[/math]
• Actual label: 1 → No misclassification

Since there are no misclassifications in the second iteration, the perceptron has converged!

Final Result

• Weights after convergence: [math]\displaystyle{ w_0 = -0.1, w_1 = 0.1, w_2 = 0.1 }[/math]
• Total cost after convergence: [math]\displaystyle{ Cost = 0 }[/math], since no misclassified points.

Exercise 2.5

Level: * (Moderate)

Exercise Types: Novel

Question

Consider a Feed-Forward Neural Network (FFN) with one or more hidden layers. Answer the following questions:

(a) Describe how does the Feed-Forward Neural Network (FFN) work in general. Describe the component of the Network.

(b) How does the forward pass work ? Provide the relevant formulas for each step.

(c) How does the backward pass (backpropagation) ? Explain and provide the formulas for each step.

Solution

(a): A Feed-Forward Neural Network (FFN) consists of an input layer, one or more hidden layers, and one output layer. Each layer transforms the input data, with each neuron's output being fed to the next layer as input. Each neuron in a layer is a perceptron, which is a basic computational unit that contains weights, bias and an activation function. The perceptron computes a weighted sum of its inputs, adds a bias term, and passes the result through an activation function. In this structure, each layer transforms the data as it passes through, with each neuron's output being fed to the next layer. The final output is the network’s prediction, then the loss function use the prediction and the true label of the data to calculate the loss. The backward pass computes the gradients of the loss with respect to each weight and bias in the network, and then update the weights and biases to minimize the loss. This process is repeated for each sample (or mini-batch) of data until the loss converges and the weights are optimized.

(b): The forward pass involves computing the output for each layer in the network. For each layer, the algorithm performs the following steps:

1. Compute the weighted sum of inputs to the layer:

[math]\displaystyle{ z^{(l)} = W^{(l)} a^{(l-1)} + b^{(l)} }[/math]

2. Use the activation function to calculate the output of the layer:

[math]\displaystyle{ \hat{y} = a^{(L)} = \sigma(z^{(L)}) }[/math]

3. Repeat these steps for each layer, until getting to the output layer

(c): The backward pass (backpropagation) updates the gradients of the loss function with respect to each weight and bias, and then use the gradient descents to update the weights.

1. Calculate the errors for each layer:

Error at the output layer: The error term at the output layer has this formula:

[math]\displaystyle{ \delta^{(L)} = \frac{\partial \mathcal{L}}{\partial a^{(L)}} \cdot \sigma'(z^{(L)}) }[/math]

Error for the hidden layers: The error for each hidden layer is:

[math]\displaystyle{ \delta^{(l)} = \left( W^{(l+1)} \right)^T \delta^{(l+1)} \cdot \sigma'(z^{(l)}) }[/math]

3. Gradient of the loss with respect to weights and biases. Compute the gradients for the weights and biases:

The gradient for weights is:

[math]\displaystyle{ \frac{\partial \mathcal{L}}{\partial W^{(l)}} = a^{(l-1)} \cdot (\delta^{(l)})^T }[/math]

The gradient is for biases is:

[math]\displaystyle{ \frac{\partial \mathcal{L}}{\partial b^{(l)}} = \delta^{(l)} }[/math]

4. Update the weights and biases using gradient descent:

[math]\displaystyle{ W^{(l)} \leftarrow W^{(l)} - \rho \cdot \frac{\partial \mathcal{L}}{\partial W^{(l)}} }[/math]

Where [math]\displaystyle{ \rho }[/math] is the learning rate.

[math]\displaystyle{ b^{(l)} \leftarrow b^{(l)} - \rho \cdot \frac{\partial \mathcal{L}}{\partial b^{(l)}} }[/math]

Repeat these steps for each layers from output layer to input layers to update all the weights and biases

Exercise 2.6

Level: * (Easy)

Exercise Types: Novel

Question

A single neuron takes an input vector [math]\displaystyle{ x=[2,-3] }[/math], with weights [math]\displaystyle{ w=[0.4,-0.6] }[/math]. The target output is [math]\displaystyle{ y_{\text{true}}=1 }[/math].

1. Calculate the weighted sum [math]\displaystyle{ z = w \cdot x }[/math].

2. Compute the squared error loss: [math]\displaystyle{ L = 0.5 \cdot (z - y_{\text{true}})^2 }[/math]

3. Find the gradient of the loss with respect to the weights [math]\displaystyle{ w }[/math] and perform one step of gradient descent with a learning rate [math]\displaystyle{ \eta = 0.01 }[/math].

4.Provide the updated weights and the error after the update.

5. Compare the result of the previous step with the case of a learning rate of [math]\displaystyle{ \eta = 0.1 }[/math]

Solution

1. [math]\displaystyle{ z = w \cdot x = (0.4 \cdot 2) + (-0.6 \cdot -3) = 0.8 + 1.8 = 2.6 }[/math]

2. [math]\displaystyle{ L = 0.5 \cdot (z - y_{\text{true}})^2 = 0.5 \cdot (2.6 - 1)^2 = 0.5 \cdot (1.6)^2 = 0.5 \cdot 2.56 = 1.28 }[/math]

3. The gradient of the loss with respect to [math]\displaystyle{ w_i }[/math] is: [math]\displaystyle{ \frac{\partial L}{\partial w_i} = (z - y_{\text{true}}) \cdot x_i }[/math]

For [math]\displaystyle{ w_1 }[/math] (associated with [math]\displaystyle{ x_1 = 2 }[/math]): [math]\displaystyle{ \frac{\partial L}{\partial w_1} = (2.6 - 1) \cdot 2 = 1.6 \cdot 2 = 3.2 }[/math]

For [math]\displaystyle{ w_2 }[/math] (associated with [math]\displaystyle{ x_2 = -3 }[/math]): [math]\displaystyle{ \frac{\partial L}{\partial w_2} = (2.6 - 1) \cdot (-3) = 1.6 \cdot -3 = -4.8 }[/math] The updated weights are: [math]\displaystyle{ w_i = w_i - \eta \cdot \frac{\partial L}{\partial w_i} }[/math]

For [math]\displaystyle{ w_1 }[/math]: [math]\displaystyle{ w_1 = 0.4 - 0.01 \cdot 3.2 = 0.4 - 0.032 = 0.368 }[/math]

For [math]\displaystyle{ w_2 }[/math]: [math]\displaystyle{ w_2 = -0.6 - 0.01 \cdot (-4.8) = -0.6 + 0.048 = -0.552 }[/math]

4. Recalculate [math]\displaystyle{ z }[/math] with updated weights: [math]\displaystyle{ z = (0.368 \cdot 2) + (-0.552 \cdot -3) = 0.736 + 1.656 = 2.392 }[/math]

Recalculate the error: [math]\displaystyle{ L = 0.5 \cdot (z - y_{\text{true}})^2 = 0.5 \cdot (2.392 - 1)^2 = 0.5 \cdot (1.392)^2 = 0.5 \cdot 1.937 = 0.968 }[/math]

5. Compare the result of the previous step with the case of a learning rate of [math]\displaystyle{ \eta = 0.1 }[/math]:

For [math]\displaystyle{ w_1 }[/math]: [math]\displaystyle{ w_1 = 0.4 - 0.1 \cdot 3.2 = 0.4 - 0.032 = 0.08 }[/math]

For [math]\displaystyle{ w_2 }[/math]: [math]\displaystyle{ w_2 = -0.6 - 0.1 \cdot (-4.8) = -0.6 + 0.048 = -0.12 }[/math]

Recalculate [math]\displaystyle{ z }[/math] with the updated weights: [math]\displaystyle{ z = (0.08 \cdot 2) + (-0.12 \cdot -3) = 0.16 + 0.36 = 0.52 }[/math]

Recalculate the error: [math]\displaystyle{ L = 0.5 \cdot (z - y_{\text{true}})^2 = 0.5 \cdot (0.52 - 1)^2 = 0.5 \cdot (-0.48)^2 = 0.5 \cdot 0.2304 = 0.1152 }[/math]

Comparison:

- With a learning rate of [math]\displaystyle{ \eta = 0.01 }[/math], the error after one update is [math]\displaystyle{ L = 0.968 }[/math].

- With [math]\displaystyle{ \eta = 0.1 }[/math], the error after one update is [math]\displaystyle{ L = 0.1152 }[/math].

The error is much lower when using a larger learning rate [math]\displaystyle{ \eta = 0.1 }[/math] compared to a smaller learning rate [math]\displaystyle{ \eta = 0.01 }[/math]. However, large learning rates can sometimes cause overshooting of the optimal solution, so care must be taken when selecting a learning rate.

Exercise 2.7

Level: * (Easy)

Exercise Types: Copied

References: https://www.uni-weimar.de/fileadmin/user/fak/medien/professuren/Webis/teaching/ws13/ml/exercises-en-neural-networks.pdf

This problem comes from Exercise 2 : Perceptron Learning.

Question

Given two single perceptrons [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] each of which defined by the inequality [math]\displaystyle{ w_0 + w_1x_1 + w_2x_2 ≥ 0 }[/math], perceptron [math]\displaystyle{ a }[/math] has the weights [math]\displaystyle{ w_0 = 1 }[/math], [math]\displaystyle{ w_1 = 2 }[/math], [math]\displaystyle{ w_2 = 1 }[/math], perceptron [math]\displaystyle{ b }[/math] has the weights [math]\displaystyle{ w_0 = 0 }[/math], [math]\displaystyle{ w_1 = 2 }[/math], [math]\displaystyle{ w_2 = 1 }[/math]. Is perceptron [math]\displaystyle{ a }[/math] more general than perceptron [math]\displaystyle{ b }[/math]?

Solution

To determine whether perceptron [math]\displaystyle{ a }[/math] is more general than perceptron [math]\displaystyle{ b }[/math], we need to examine their decision boundaries and the regions they classify as "positive" (where [math]\displaystyle{ w_0 + w_1x_1 + w_2x_2 \geq 0 }[/math]).

The decision boundaries for both perceptrons are defined by: [math]\displaystyle{ w_0 + w_1x_1 + w_2x_2 = 0 }[/math].

For Perceptron [math]\displaystyle{ a }[/math]: [math]\displaystyle{ 1 + 2x_1 + x_2 \geq 0 }[/math]; the decision boundary is: [math]\displaystyle{ x_2 = -2x_1 - 1 }[/math].

For Perceptron [math]\displaystyle{ b }[/math]: [math]\displaystyle{ 2x_1 + x_2 \geq 0 }[/math]; the decision boundary is: [math]\displaystyle{ x_2 = -2x_1 }[/math].

We want to clarify what does more general mean. If perceptron [math]\displaystyle{ a }[/math] classifies every point classified positively by perceptron [math]\displaystyle{ b }[/math] as positive, then [math]\displaystyle{ a }[/math] is at least as general as [math]\displaystyle{ b }[/math]. If in addition, [math]\displaystyle{ a }[/math] classifies points as positive that [math]\displaystyle{ b }[/math] does not, then [math]\displaystyle{ a }[/math] is strictly more general.

Apparently perceptron [math]\displaystyle{ a }[/math]'s positive region includes all points that satisfy [math]\displaystyle{ x_2 \geq -2x_1 - 1 }[/math], which is strictly larger than [math]\displaystyle{ b }[/math]'s region because [math]\displaystyle{ -2x_1 - 1 \lt -2x_1 }[/math] for all [math]\displaystyle{ x_1 }[/math]; perceptron [math]\displaystyle{ b }[/math]'s positive region includes all points that satisfy [math]\displaystyle{ x_2 \geq -2x_1 }[/math], which is a subset of [math]\displaystyle{ a }[/math]'s region.

Therefore, perceptron [math]\displaystyle{ a }[/math] is more general than perceptron [math]\displaystyle{ b }[/math] because all points classified as positive by [math]\displaystyle{ b }[/math] are also classified as positive by [math]\displaystyle{ a }[/math], and [math]\displaystyle{ a }[/math] classifies additional points (where [math]\displaystyle{ -2x_1 - 1 \leq x_2 \lt -2x_1 }[/math]) as positive that [math]\displaystyle{ b }[/math] does not.

Exercise 2.10

Level: * (Easy)

Exercise Type: Novel

Question

In a simple linear regression

a). Derive the vectorized form of the SSE (loss function) in terms of [math]\displaystyle{ Y }[/math], [math]\displaystyle{ X }[/math] and [math]\displaystyle{ \theta }[/math].

b). Find the equation which minimizes [math]\displaystyle{ \theta }[/math] (Recall that this is the weights of the linear regression).

Solution

a).

[math]\displaystyle{ \begin{align*} SSE &= (Y - \hat{Y})^2 \\ &= (Y - \hat{Y})^T (Y - \hat{Y}) \\ &= Y^TY - Y^TX\theta - (X\theta)^T Y + (X\theta)^T(X\theta) \\ &= Y^TY - 2Y^TX\theta + (X\theta)^T(X\theta) \\ \end{align*} }[/math]

b).

[math]\displaystyle{ \begin{align*} 0 &= \frac{\partial SSE}{\partial \theta} \\ 0 &= \frac{\partial}{\partial \theta} \Big[ Y^TY - 2Y^TX\theta + (X\theta)^T(X\theta)\Big] \\ 0 &= 0 - 2YX^T + 2X^TX\theta \\ 2X^TX\theta &= 2YX^T \\ \theta &= (YX^T)(X^TX)^{-1} \end{align*} }[/math]

Exercise 2.11

Level: Moderate

Exercise Types: Novel

Question

Deep learning models often face challenges during training due to the vanishing gradient problem, especially when using sigmoid or tanh activation functions.

(a) Describe the vanishing gradient problem and its impact on the training of deep networks.

(b) Explain how the introduction of ReLU (Rectified Linear Unit) activation function mitigates this problem.

(c) Discuss one potential downside of using ReLU and propose an alternative activation function that addresses this limitation.

Solution

(a) Vanishing Gradient Problem: The vanishing gradient problem occurs when the gradients of the loss function become extremely small as they are propagated back through the layers of a deep network. This leads to:

Slow or stagnant weight updates in early layers. Difficulty in effectively training deep models. This issue is particularly pronounced with activation functions like sigmoid and tanh, where gradients approach zero as inputs saturate.

(b) Role of ReLU in Mitigation: ReLU, defined as [math]\displaystyle{ f(x) = \max(0, x) }[/math], mitigates the vanishing gradient problem by:

Producing non-zero gradients for positive inputs, maintaining effective weight updates. Introducing sparsity, as neurons deactivate (output zero) for negative inputs, which improves model efficiency.

(c) Downside of ReLU and Alternatives: One downside of ReLU is the "dying ReLU" problem, where neurons output zero for all inputs, effectively becoming inactive. This can happen when weights are poorly initialized or during training.

Alternative: Leaky ReLU allows a small gradient for negative inputs, defined as [math]\displaystyle{ f(x) = x }[/math] for [math]\displaystyle{ x \gt 0 }[/math] and [math]\displaystyle{ f(x) = \alpha x }[/math] for [math]\displaystyle{ x \leq 0 }[/math], where [math]\displaystyle{ \alpha }[/math] is a small positive constant. This prevents neurons from dying, ensuring all neurons contribute to learning.

Exercise 3.1

Level: ** (Moderate)

Exercise Type: Novel

Implement the perceptron learning algorithm with momentum for the AND function. Plot the decision boundary after 10 epochs of training with a learning rate of 0.1 and a momentum of 0.9.

Solution

import numpy as np
import matplotlib.pyplot as plt

# Dataset
data = np.array([
    [0, 0, -1],
    [0, 1, -1],
    [1, 0, -1],
    [1, 1, 1]
])

# Initialize weights, learning rate, and momentum
weights = np.random.rand(3)
learning_rate = 0.1
momentum = 0.9
epochs = 10
previous_update = np.zeros(3)

# Add bias term to data
X = np.hstack((np.ones((data.shape[0], 1)), data[:, :2]))
y = data[:, 2]

# Training loop
for epoch in range(epochs):
    for i in range(len(X)):
        prediction = np.sign(np.dot(weights, X[i]))
        if prediction != y[i]:
            update = learning_rate * y[i] * X[i] + momentum * previous_update
            weights += update
            previous_update = update

# Plot final decision boundary
x_vals = np.linspace(-0.5, 1.5, 100)
y_vals = -(weights[1] * x_vals + weights[0]) / weights[2]
plt.plot(x_vals, y_vals, label='Final Decision Boundary')

# Plot dataset
for point in data:
    color = 'blue' if point[2] == 1 else 'red'
    plt.scatter(point[0], point[1], color=color)

plt.title('Perceptron with Momentum')
plt.legend()
plt.show()

Final decision boundary.

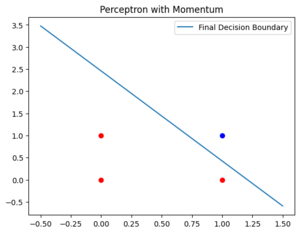
Exercise 3.2

Level: ** (Moderate)

Exercise Types: Novel

Question

Write a python program showing how the back propagation algorithm work with a 2 inputs 2 hidden layer and 1 output layer neural network. Train the network on the XOR problem:

• Input[0,0] -> Output 0
• Input [0,1] -> Output 1
• Input [1,0] -> Output 1
• Input [1,1] -> Output 0

Use the sigmoid activation function. Use Mean Square Error as the loss function.

Solution

import numpy as np

# -------------------------
# 1. Define Activation Functions
# -------------------------

def sigmoid(x):
    """
    Sigmoid activation function.
    """
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    """
    Derivative of the sigmoid function.
    Here, 'x' is assumed to be sigmoid(x), 
    meaning x is already the output of the sigmoid.
    """
    return x * (1 - x)


# -------------------------
# 2. Prepare the Training Data (XOR)
# -------------------------
# Input data (4 samples, each with 2 features)
X = np.array([
    [0, 0],
    [0, 1],
    [1, 0],
    [1, 1]
])

# Target labels (4 samples, each is a single output)
y = np.array([
    [0],
    [1],
    [1],
    [0]
])

# -------------------------
# 3. Initialize Network Parameters
# -------------------------
# Weights for input -> hidden (shape: 2x2)
W1 = np.random.randn(2, 2)
# Bias for hidden layer (shape: 1x2)
b1 = np.random.randn(1, 2)

# Weights for hidden -> output (shape: 2x1)
W2 = np.random.randn(2, 1)
# Bias for output layer (shape: 1x1)
b2 = np.random.randn(1, 1)

# Hyperparameters
learning_rate = 0.1
num_epochs = 10000

# -------------------------
# 4. Training Loop
# -------------------------
for epoch in range(num_epochs):
    # 4.1. Forward Pass
    #   - Compute hidden layer output
    hidden_input = np.dot(X, W1) + b1  # shape: (4, 2)
    hidden_output = sigmoid(hidden_input)
    
    #   - Compute final output
    final_input = np.dot(hidden_output, W2) + b2  # shape: (4, 1)
    final_output = sigmoid(final_input)
    
    # 4.2. Compute Loss (Mean Squared Error)
    error = y - final_output  # shape: (4, 1)
    loss = np.mean(error**2)
    
    # 4.3. Backpropagation
    #   - Gradient of loss w.r.t. final_output
    d_final_output = error * sigmoid_derivative(final_output)  # shape: (4, 1)
    
    #   - Propagate error back to hidden layer
    error_hidden_layer = np.dot(d_final_output, W2.T)  # shape: (4, 2)
    d_hidden_output = error_hidden_layer * sigmoid_derivative(hidden_output)  # shape: (4, 2)
    
    # 4.4. Gradient Descent Updates
    #   - Update W2, b2
    W2 += learning_rate * np.dot(hidden_output.T, d_final_output)  # shape: (2, 1)
    b2 += learning_rate * np.sum(d_final_output, axis=0, keepdims=True)  # shape: (1, 1)
    
    #   - Update W1, b1
    W1 += learning_rate * np.dot(X.T, d_hidden_output)  # shape: (2, 2)
    b1 += learning_rate * np.sum(d_hidden_output, axis=0, keepdims=True)  # shape: (1, 2)
    
    # Print loss every 1000 epochs
    if epoch % 1000 == 0:
        print(f"Epoch {epoch}, Loss: {loss:.6f}")

# -------------------------
# 5. Testing / Final Outputs
# -------------------------
print("\nTraining complete.")
print("Final loss:", loss)

# Feedforward one last time to see predictions
hidden_output = sigmoid(np.dot(X, W1) + b1)
final_output = sigmoid(np.dot(hidden_output, W2) + b2)

print("\nOutput after training:")
for i, inp in enumerate(X):
    print(f"Input: {inp} -> Predicted: {final_output[i][0]:.4f} (Target: {y[i][0]})")

Output:

Epoch 0, Loss: 0.257193
Epoch 1000, Loss: 0.247720
Epoch 2000, Loss: 0.226962
Epoch 3000, Loss: 0.191367
Epoch 4000, Loss: 0.162169
Epoch 5000, Loss: 0.034894
Epoch 6000, Loss: 0.012459
Epoch 7000, Loss: 0.007127
Epoch 8000, Loss: 0.004890
Epoch 9000, Loss: 0.003687

Training complete.
Final loss: 0.0029435579049382756

Output after training:
Input: [0 0] -> Predicted: 0.0598 (Target: 0)
Input: [0 1] -> Predicted: 0.9461 (Target: 1)
Input: [1 0] -> Predicted: 0.9506 (Target: 1)
Input: [1 1] -> Predicted: 0.0534 (Target: 0)

Exercise 3.3

Level: * (Easy)

Exercise Types: Novel

Question

Implement 4 iterations of gradient descent with and without momentum for the function [math]\displaystyle{ f(x) = x^2 + 2 }[/math] with learning rate [math]\displaystyle{ \eta=0.1 }[/math], momentum [math]\displaystyle{ \gamma=0.9 }[/math], starting value of [math]\displaystyle{ x_0=2 }[/math], starting velocity of [math]\displaystyle{ v_0=0 }[/math]. Comment on the differences.

Solution

Note that [math]\displaystyle{ f'(x) = 2x }[/math]

Without momentum:

Iteration 1: [math]\displaystyle{ x_1 = x_0 - \eta* f'(x_0) = 2 - 0.1*2*2 = 1.6 }[/math]

Iteration 2: [math]\displaystyle{ x_2 = x_1 - \eta* f'(x_1) = 1.6 - 0.1*2*1.6 = 1.28 }[/math]

Iteration 3: [math]\displaystyle{ x_3 = x_2 - \eta* f'(x_2) = 1.28 - 0.1*2*1.28 = 1.024 }[/math]

Iteration 4: [math]\displaystyle{ x_4 = x_3 - \eta* f'(x_3) =1.024 - 0.1*2*1.024 = 0.8192 }[/math]

With momentum:

Iteration 1: [math]\displaystyle{ v_1 = \gamma*v_0 + \eta * f'(x_0) = 0.9*0 + 0.1*2*2 = 0.4, x_1 = x_0-v_1 = 2-0.4 = 1.6 }[/math]

Iteration 2: [math]\displaystyle{ v_2 = \gamma*v_1 + \eta * f'(x_1) = 0.9*0.4+0.1*2*1.6 = 0.68, x_2 = x_1-v_2 = 1.6-0.68 = 0.92 }[/math]

Iteration 3: [math]\displaystyle{ v_3 = \gamma*v_2 + \eta * f'(x_2) = 0.9*0.68 + 0.1*2*0.92 = 0.796, x_3 = x_2-v_3 = 0.92-0.796 = 0.124 }[/math]

Iteration 4: [math]\displaystyle{ v_4 = \gamma*v_3 + \eta * f'(x_3) = 0.9*0.796 + 0.1*2*0.124 = 0.7412, x_4 = x_3-v_4 = 0.124 - 0.7412 = -0.6172 }[/math]

By observation, we know that the minimum of [math]\displaystyle{ f(x)=x^2+2 }[/math] occurs at [math]\displaystyle{ x=0 }[/math]. We can see that with momentum, the algorithm moves towards the minimum much faster than without momentum as past gradients are accumulated, leading to larger steps. However, we also can see that momentum can cause the algorithm to overshoot the minimum since we are taking larger steps.

Benefits for momentum: Momentum is a technique used in optimization to accelerate convergence. Inspired by physical momentum, it helps in navigating the optimization landscape.

By remembering the direction of previous gradients, which are accumulated into a running average (the velocity), momentum helps guide the updates more smoothly, leading to faster progress. This running average allows the optimizer to maintain a consistent direction even if individual gradients fluctuate. Additionally, momentum can help the algorithm escape from shallow local minima by carrying the updates through flat regions. This prevents the optimizer from getting stuck in small, unimportant minima and helps it continue moving toward a better local minimum.

Additional Comment: It is important to note that the use of running average is only there to help with intuition. At time t, while the velocity is a linear sum of previous gradients, the weight of the gradient decreases as time get further away. That is, the [math]\displaystyle{ \nabla Q(w_0) }[/math] term will have a coefficient of [math]\displaystyle{ (1-\gamma)^{t} }[/math].

Exercise 3.4

Level: ** (Moderate)

Exercise Types: Novel

Question

Perform one iteration of forward pass and backward propagation for the following network:

• Input layer: 2 neurons (x₁, x₂)
• Hidden layer: 2 neurons (h₁, h₂)
• Output layer: 1 neuron (ŷ)

• Input-to-Hidden Layer:

 w₁₁¹ = 0.15, w₂₁¹ = 0.20, w₁₂¹ = 0.25, w₂₂¹ = 0.30
 Bias: b¹ = 0.35
 Activation function: sigmoid

• Hidden-to-Output Layer:

 w₁₁² = 0.40, w₂₁² = 0.45
 Bias: b² = 0.60
 Activation function: sigmoid

Input:

• x₁ = 0.05, x₂ = 0.10
• Target output: y = 0.01
• Learning rate: η = 0.5

Solution

Step 1: Forward Pass

1. Hidden Layer Outputs

For neuron h₁:

• [math]\displaystyle{ z₁¹ = w₁₁¹ \cdot x₁ + w₂₁¹ \cdot x₂ + b¹ = 0.15(0.05) + 0.20(0.10) + 0.35 = 0.3775 }[/math]
• [math]\displaystyle{ h₁ = \sigma(z₁¹) = \frac{1}{1 + e^{-0.3775}} \approx 0.5933 }[/math]

For neuron h₂:

• [math]\displaystyle{ z₂¹ = w₁₂¹ \cdot x₁ + w₂₂¹ \cdot x₂ + b¹ = 0.25(0.05) + 0.30(0.10) + 0.35 = 0.3925 }[/math]
• [math]\displaystyle{ h₂ = \sigma(z₂¹) = \frac{1}{1 + e^{-0.3925}} \approx 0.5968 }[/math]

2. Output Layer

• [math]\displaystyle{ z² = w₁₁² \cdot h₁ + w₂₁² \cdot h₂ + b² = 0.40(0.5933) + 0.45(0.5968) + 0.60 = 1.1051 }[/math]
• [math]\displaystyle{ \hat{y} = \sigma(z²) = \frac{1}{1 + e^{-1.1051}} \approx 0.7511 }[/math]

Step 2: Compute Error

• [math]\displaystyle{ E = \frac{1}{2} (\hat{y} - y)^2 = \frac{1}{2} (0.7511 - 0.01)^2 \approx 0.2738 }[/math]

Step 3: Backpropagation

3.1: Gradients for Output Layer

1. Gradient w.r.t. output neuron:

• [math]\displaystyle{ \delta² = (\hat{y} - y) \cdot \hat{y} \cdot (1 - \hat{y}) }[/math]
• [math]\displaystyle{ \delta² = (0.7511 - 0.01) \cdot 0.7511 \cdot (1 - 0.7511) = 0.1381 }[/math]

2. Update weights and bias for hidden-to-output layer:

• [math]\displaystyle{ w₁₁² = w₁₁² - \eta \cdot \delta² \cdot h₁ = 0.40 - 0.5 \cdot 0.1381 \cdot 0.5933 = 0.359 }[/math]
• [math]\displaystyle{ w₂₁² = w₂₁² - \eta \cdot \delta² \cdot h₂ = 0.45 - 0.5 \cdot 0.1381 \cdot 0.5968 = 0.409 }[/math]
• [math]\displaystyle{ b² = b² - \eta \cdot \delta² = 0.60 - 0.5 \cdot 0.1381 = 0.53095 }[/math]

3.2: Gradients for Hidden Layer

1. Gradients for hidden layer neurons:

For h₁:

• [math]\displaystyle{ \delta₁ = \delta² \cdot w₁₁² \cdot h₁ \cdot (1 - h₁) }[/math]
• [math]\displaystyle{ \delta₁ = 0.1381 \cdot 0.40 \cdot 0.5933 \cdot (1 - 0.5933) = 0.0138 }[/math]

For h₂:

• [math]\displaystyle{ \delta₂ = \delta² \cdot w₂₁² \cdot h₂ \cdot (1 - h₂) }[/math]
• [math]\displaystyle{ \delta₂ = 0.1381 \cdot 0.45 \cdot 0.5968 \cdot (1 - 0.5968) = 0.0148 }[/math]

2. Update weights and bias for input-to-hidden layer:

For w₁₁¹:

• [math]\displaystyle{ w₁₁¹ = w₁₁¹ - \eta \cdot \delta₁ \cdot x₁ = 0.15 - 0.5 \cdot 0.0138 \cdot 0.05 = 0.14965 }[/math]

For w₂₁¹:

• [math]\displaystyle{ w₂₁¹ = w₂₁¹ - \eta \cdot \delta₁ \cdot x₂ = 0.20 - 0.5 \cdot 0.0138 \cdot 0.10 = 0.19931 }[/math]

For b¹:

• [math]\displaystyle{ b¹ = b¹ - \eta \cdot (\delta₁ + \delta₂) = 0.35 - 0.5 \cdot (0.0138 + 0.0148) = 0.3347 }[/math]

This completes one iteration of forward and backward propagation.

Exercise 3.5

Level: * (Easy)

Exercise Types: Novel

Question

Consider the loss function [math]\displaystyle{ Q(w) = w^2 + 2w + 1 }[/math]. Compute the gradient of [math]\displaystyle{ Q(w) }[/math]. Starting from [math]\displaystyle{ w_0 = 2 }[/math], perform two iterations of stochastic gradient descent using a learning rate [math]\displaystyle{ \rho = 0.1 }[/math].

Solution

Compute the gradient at [math]\displaystyle{ w_0 }[/math]:[math]\displaystyle{ \nabla Q(w_0) = \frac{d}{dw_0}(w_0^2 + 2w_0 + 1) = 2w_0 + 2 = 2(2) + 2 = 4 + 2 = 6 }[/math]

Update the weight using SGD: [math]\displaystyle{ w_1 = w_0 - \rho \cdot \nabla Q(w_0) = 2 - 0.1 \cdot 6 = 2 - 0.6 = 1.4 }[/math]

Compute the gradient at [math]\displaystyle{ w_1 }[/math]: [math]\displaystyle{ \nabla Q(w_1) = \frac{d}{dw_1}(w_1^2 + 2w_1 + 1) = 2w_1 + 2 = 2(1.4) + 2 = 2.8 + 2 = 4.8 }[/math]

Update the weight again: [math]\displaystyle{ w_2 = w_1 - \rho \cdot \nabla Q(w_1) = 1.4 - 0.1 \cdot 4.8 = 1.4 - 0.48 = 0.92 }[/math]

Gradient Path Figure:

Gradient Descent Path on Loss Function

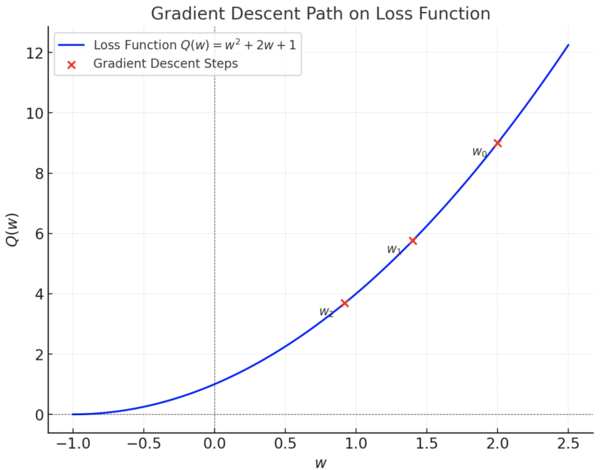
Exercise 3.6

Level: * (Easy)

Exercise Types: Novel

Question

What is the prediction of the following MLP for [math]\displaystyle{ x = \begin{bmatrix} 2 \\ 2 \\ 1 \end{bmatrix} }[/math]?

Diagram of the MLP

Both layers are using sigmoid activation. The weight matrices connecting the input and hidden layer, and the hidden layer and output are respectively: [math]\displaystyle{ V = \begin{bmatrix} 1 & 0 & 1 \\ 1 & -1 & 0 \end{bmatrix}, \quad W = \begin{bmatrix} 0 & 1 \end{bmatrix}. }[/math]

Choose the correct answer:
a) [math]\displaystyle{ \sigma(0) }[/math]
b) [math]\displaystyle{ \sigma(\sigma(0)) }[/math]
c) [math]\displaystyle{ \sigma(-1) }[/math]
d) [math]\displaystyle{ \sigma(\sigma(0)) }[/math]

Solution

The correct answer is b): [math]\displaystyle{ \sigma(\sigma(0)) }[/math].

Calculation

Step 1: Compute the hidden layer output [math]\displaystyle{ h }[/math].
[math]\displaystyle{ h = \sigma(Vx) = \begin{bmatrix} \sigma(3) \\ \sigma(0) \end{bmatrix} }[/math]

Step 2: Compute the output layer prediction [math]\displaystyle{ y }[/math].
[math]\displaystyle{ y = \sigma(Wh) = \sigma(\sigma(0)) }[/math]

Thus, the prediction of the MLP is [math]\displaystyle{ \sigma(\sigma(0)) }[/math].

Exercise 3.7

Level: * (Easy)

Exercise Types: Novel

Question

Feedforward Neural Networks (FNNs) are one of the commonly used model in deep learning. In the context of training such networks, there are some important parameters we can choose.

1. (a): Give three commonly used activation functions, along with their formulas and when to use them.
2. (b): Write down a widely used loss function for classification and why it is popular.
3. (c): Explain what is adaptive learning methods and how they help optimize and speed up network training.

Solution

(a)

1. Sigmoid Activation Function

   [math]\displaystyle{ f(z) = \frac{1}{1 + e^{-z}} }[/math]

   Usage: Output ranges from 0 to 1, suitable for estimating probabilities.

2. ReLU (Rectified Linear Unit) Activation Function

   [math]\displaystyle{ f(z) = \max(0, z) }[/math]

   Outputs zero or a positive number, enabling some weights to be set to 0, promoting sparse representation

(b)

Cross-Entropy Loss
[math]\displaystyle{ \mathcal{L}_{\text{CE}} = -\sum_{i=1}^{n} \bigl[\, y_i \log\bigl(y_{\text{pred},i}\bigr)\ +\ (1 - y_i)\,\log\bigl(1 - y_{\text{pred},i}\bigr) \bigr] }[/math]

It provides a smooth and continuous gradient, and it penalizes the incorrect predictions more when the predictions are made with confidence. It is well suited for multi-class classification, especially when used with softmax function together.

(c)

Some variants of SGD adjust the learning rate during the training process based on the gradients' magnitudes, helping accelerate convergence and manage gradients more effectively.

Exercise 3.8

Level: * (Easy)

Exercise Types: Novel

Question

Consider a Feedforward Neural Network (FNN) with a single neuron, where the loss function is given by: [math]\displaystyle{ L(w)=(w-3)^2 }[/math]. Compute the gradient of [math]\displaystyle{ L(w) }[/math]. Starting from [math]\displaystyle{ w_{0}=0 }[/math] perform two iterations of Stochastic Gradient Descent (SGD) using a learning rate [math]\displaystyle{ \eta = 0.5 }[/math]

Solution

Gradient of [math]\displaystyle{ L(w) }[/math]:
[math]\displaystyle{ \frac{dL}{dw}=2(w-3) }[/math]
[math]\displaystyle{ w_{0}=0 }[/math]
[math]\displaystyle{ w_{1}=w_{0}-\eta \frac{dL}{dw}=3 }[/math]
[math]\displaystyle{ w_{2}=w_{1}-\eta \frac{dL}{dw}=3 }[/math]
So, after 2 iterations, [math]\displaystyle{ w_{2}=3 }[/math].

Exercise 3.9

Level: ** (Moderate)

Exercise Types: Modified

References: Source: Schonlau, M., Applied Statistical Learning. With Case Studies in Stata, Springer. ISBN 978-3-031-33389-7 (Chapter 14, page 318).

Question

Consider the feedforward neural network with initial weights shown in Figure 3.9 (For simplicity, there are no biases). Use sigmoid activation functions for both the hidden and the output layers. Use a learning rate of [math]\displaystyle{ \rho= 0.5 }[/math].

Figure 3.9

(a): Compute a forward pass through the network for the observation (y,x1,x2,x3) = (1,3,-2,5). That is, compute the predicted probability [math]\displaystyle{ p_1 }[/math].

(b): Using the result from (a), make a backward pass to compute the revised w7 and w1. Use squared error loss: [math]\displaystyle{ E = 0.5 * (y-p_1)^2 }[/math], where [math]\displaystyle{ y\in \{0,1\} }[/math] is the true value of the response and [math]\displaystyle{ p_1 }[/math] is the predicted probability.

Solution

(a)

[math]\displaystyle{ z_A = x_1w_1 + x_2w_2 + x_3w_3 = 3*0.8+(-2)*(-1)+5*0.1=4.9 }[/math]

[math]\displaystyle{ z_B = x_1w_4 + x_2w_5 + x_3w_6 = 3*0.3+(-2)*0.5+5*(-0.2)=-1.1 }[/math]

[math]\displaystyle{ out_A = \frac{1}{1+e^{-z_A}} = \frac{1}{1+e^{-4.9}} = 0.9926 }[/math]

[math]\displaystyle{ out_B = \frac{1}{1+e^{-z_B}} = \frac{1}{1+e^{1.1}} = 0.2497 }[/math]

[math]\displaystyle{ z_1 = out_Aw_7+out_Bw_8=0.9926*1.3+0.2497*0.4=1.3903 }[/math]

[math]\displaystyle{ p_1 = \frac{1}{1+e^{-z_1}} = \frac{1}{1+e^{-1.3903}} =0.8006 }[/math]

(b)

[math]\displaystyle{ \frac{\partial{E}}{\partial{w_7}}=\frac{\partial{E}}{\partial{p_1}}\frac{\partial{p_1}}{\partial{z_1}}\frac{\partial{z_1}}{\partial{w_7}}=(p_1-y)*p_1*(1-p_1)*out_A=-0.0317 }[/math]

[math]\displaystyle{ w_7^{new} = 1.3-0.5*(-0.0317)=1.3159 }[/math]

[math]\displaystyle{ \frac{\partial{E}}{\partial{w_1}}=\frac{\partial{E}}{\partial{p_1}}\frac{\partial{p_1}}{\partial{z_1}}\frac{\partial{z_1}}{\partial{out_A}}\frac{\partial{out_A}}{\partial{z_A}}\frac{\partial{z_A}}{\partial{w_1}}=(p_1-y)*p_1*(1-p_1)*w_7*out_A*(1-out_A)*x_1=-0.0091 }[/math]

[math]\displaystyle{ w_1^{new} = 0.8-0.5*(-0.0091)=0.8046 }[/math]

Exercise 3.10

Level: ** (Easy)

Exercise Types: (Novel)

Question

What is vanishing gradient and how is it caused? What is the solution that fixes vanishing gradient?

Answer

The vanishing gradient problem occurs when the gradients used to update weights in a neural network become extremely small as they propagate backward through the layers. This happens because activation functions compress their inputs into a narrow output range. Consequently, their derivatives are very small, particularly for inputs far from zero, causing gradients to shrink exponentially in deeper layers. As a result, in modern computing, the gradient will be the result of multiplying multiple epsilon sized gradients where the resulting update is 0. To fix this, we use the relu activation function where the gradient is either 0 or 1. This ensures that the update value will not vanish due to small gradients. This is because ReLU does not squash its outputs into a narrow range. For positive inputs, the gradient of ReLU is constant and equal to 1, ensuring that gradients remain significant during backpropagation. Unlike other functions that lead to exponentially small gradients, ReLU’s piecewise linear nature avoids the compounding effect of small derivatives across layers. By maintaining larger gradient values, ReLU ensures that weight updates are not hindered, making it an effective solution to the vanishing gradient problem, especially in deep networks.

Exercise 3.11

Level: ** (Moderate)

Exercise Types: Novel

Question

Given a two-layer neural network with the following specifications:

Inputs: Represented as [math]\displaystyle{ \mathbf{x} = [x_1, x_2]^T }[/math], a [math]\displaystyle{ 2\times1 }[/math] column vector.

Weights: First layer weight matrix: [math]\displaystyle{ W_1 }[/math], a [math]\displaystyle{ 2\times2 }[/math] matrix; Second layer weight vector: [math]\displaystyle{ W_2 }[/math], a [math]\displaystyle{ 1\times2 }[/math] row vector.

Activations: The activation function for all layers is the sigmoid function, defined as: [math]\displaystyle{ \sigma(z) = \frac{1}{1 + e^{-z}} }[/math].

Loss Function: The cross-entropy loss, given by [math]\displaystyle{ L = -y \log(\hat{y}) - (1 - y) \log(1 - \hat{y}) }[/math] where [math]\displaystyle{ y }[/math] is the true label (0 or 1) and [math]\displaystyle{ \hat{y} }[/math] is the predicted output.

(a). Write out the forward propagation steps.

(b). Calculate the derivative of the loss with respect to weights in [math]\displaystyle{ W_1 }[/math] and [math]\displaystyle{ W_2 }[/math] using the chain rule.

Solution

(a). Forward Propagation Steps:

For the first layer pre-activation: [math]\displaystyle{ \mathbf{z}_1 = W_1 \cdot \mathbf{x} }[/math] where [math]\displaystyle{ \mathbf{z}_1 }[/math] is a [math]\displaystyle{ 2\times1 }[/math] column vector.

For the first layer activation: [math]\displaystyle{ \mathbf{a}_1 = \sigma(\mathbf{z}_1) }[/math] where the sigmoid function is applied element-wise, resulting in [math]\displaystyle{ \mathbf{a}_1 }[/math], a [math]\displaystyle{ 2\times1 }[/math] column vector.

For the second layer pre-activation: [math]\displaystyle{ z_2 = W_2 \cdot \mathbf{a}_1 }[/math] where [math]\displaystyle{ z_2 }[/math] is a scalar value.

For the second layer activation (output): [math]\displaystyle{ \hat{y} = \sigma(z_2) }[/math] where [math]\displaystyle{ \hat{y} }[/math] represents the predicted probability.

For the loss calculation: [math]\displaystyle{ L = -y \log(\hat{y}) - (1 - y) \log(1 - \hat{y}) }[/math].

(b). Derivative of the Loss

Gradients for the Second Layer [math]\displaystyle{ W_2 }[/math]: using the chain rule: [math]\displaystyle{ \frac{\partial L}{\partial W_2} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_2} \cdot \frac{\partial z_2}{\partial W_2}. }[/math]

For the loss gradient w.r.t. output:[math]\displaystyle{ \frac{\partial L}{\partial \hat{y}} = -\frac{y}{\hat{y}} + \frac{1 - y}{1 - \hat{y}}. }[/math]

For the gradient of sigmoid output w.r.t. pre-activation:[math]\displaystyle{ \frac{\partial \hat{y}}{\partial z_2} = \hat{y} (1 - \hat{y}). }[/math]

For the gradient of pre-activation w.r.t. weights:[math]\displaystyle{ \frac{\partial z_2}{\partial W_2} = \mathbf{a}_1. }[/math]

For the combine terms:[math]\displaystyle{ \frac{\partial L}{\partial W_2} = (\hat{y} - y) \cdot \mathbf{a}_1. }[/math]

Gradients for the First Layer [math]\displaystyle{ W_1 }[/math]: using the chain rule:[math]\displaystyle{ \frac{\partial L}{\partial W_1} = \frac{\partial L}{\partial \mathbf{a}_1} \cdot \frac{\partial \mathbf{a}_1}{\partial \mathbf{z}_1} \cdot \frac{\partial \mathbf{z}_1}{\partial W_1}. }[/math]

For the gradient of loss w.r.t. first layer activation:[math]\displaystyle{ \frac{\partial L}{\partial \mathbf{a}_1} = \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial \mathbf{a}_1} }[/math]; from the second layer:[math]\displaystyle{ \frac{\partial L}{\partial z_2} = (\hat{y} - y), \quad \frac{\partial z_2}{\partial \mathbf{a}_1} = W_2^T. }[/math] So:[math]\displaystyle{ \frac{\partial L}{\partial \mathbf{a}_1} = (\hat{y} - y) \cdot W_2^T. }[/math]

For the gradient of activation w.r.t. pre-activation: [math]\displaystyle{ \frac{\partial \mathbf{a}_1}{\partial \mathbf{z}_1} = \mathbf{a}_1 \odot (1 - \mathbf{a}_1), }[/math] where [math]\displaystyle{ \odot }[/math] denotes element-wise multiplication.

For the gradient of pre-activation w.r.t. first layer weights: [math]\displaystyle{ \frac{\partial \mathbf{z}_1}{\partial W_1} = \mathbf{x}^T. }[/math]

For the combine terms: [math]\displaystyle{ \frac{\partial L}{\partial W_1} = \left[ (\hat{y} - y) \cdot W_2^T \right] \odot \left[ \mathbf{a}_1 \odot (1 - \mathbf{a}_1) \right] \cdot \mathbf{x}^T. }[/math]

Exercise 3.12

Level: ** (Moderate)

Exercise Types: Novel

Question

Consider the **Bent Identity loss function**, a smooth approximation of the absolute loss, defined as:

[math]\displaystyle{ l(y, \hat{y}) = \sqrt{1 + (\hat{y} - y)^2} - 1 }[/math]

The following identities may be useful:

[math]\displaystyle{ \frac{d}{dx} \sqrt{1 + x^2} = \frac{x}{\sqrt{1 + x^2}}, \quad \frac{\partial y}{\partial x} = \frac{\partial y}{\partial u} \frac{\partial u}{\partial x}. }[/math]

where [math]\displaystyle{ y }[/math] is the true response, and [math]\displaystyle{ \hat{y} = w^T x + b }[/math] is the predicted response for a feature vector [math]\displaystyle{ x }[/math] given model parameters [math]\displaystyle{ w }[/math] and [math]\displaystyle{ b }[/math].

Part (a): Compute the Gradient

Find the gradient of the loss function with respect to [math]\displaystyle{ w }[/math] and [math]\displaystyle{ b }[/math].

Part (b): Implement Gradient Descent

Using your result from Part (a), write the update rules for **gradient descent** and implement the iterative optimization process.

Solution

Step 1: Computing the Gradient

We differentiate the loss function:

[math]\displaystyle{ l(y, \hat{y}) = \sqrt{1 + (\hat{y} - y)^2} - 1. }[/math]

Differentiating with respect to [math]\displaystyle{ w }[/math] and [math]\displaystyle{ b }[/math], we obtain:

[math]\displaystyle{ \nabla_w l = \frac{(\hat{y} - y) x}{\sqrt{1 + (\hat{y} - y)^2}} }[/math]

[math]\displaystyle{ \nabla_b l = \frac{\hat{y} - y}{\sqrt{1 + (\hat{y} - y)^2}} }[/math]

Step 2: Gradient Descent Update Rules

We update the parameters using gradient descent:

[math]\displaystyle{ w_{t+1} = w_t - \eta \nabla_w l }[/math]

[math]\displaystyle{ b_{t+1} = b_t - \eta \nabla_b l }[/math]

where [math]\displaystyle{ \eta }[/math] is the learning rate.

Step 3: Algorithm Implementation

Initialize w, b randomly
Set learning_rate η
For t = 1 to max_iterations:
    Compute predicted value: y_hat = w^T * x + b
    Compute gradients:
        grad_w = ((y_hat - y) / sqrt(1 + (y_hat - y)^2)) * x
        grad_b = (y_hat - y) / sqrt(1 + (y_hat - y)^2)
    Update parameters:
        w = w - η * grad_w
        b = b - η * grad_b
    Check for convergence

Exercise 3.13

Level: ** (Difficult)

Exercise Types: Novel

Question

Consider training a deep neural network with momentum-based SGD on a quadratic approximation of the loss near a local minimum, [math]\displaystyle{ L(\theta) = \tfrac{1}{2}\theta^\top H ,\theta }[/math], where [math]\displaystyle{ H }[/math] is the Hessian. Explain how the momentum term modifies the effective condition number of [math]\displaystyle{ H }[/math], and why this can speed convergence in directions with small curvature while controlling overshoot in directions with large curvature. Provide a brief analysis of the discrete iteration dynamics that illustrates this effect.

Solution

Let [math]\displaystyle{ \theta_t }[/math] be the parameters at iteration [math]\displaystyle{ t }[/math], and [math]\displaystyle{ v_t }[/math] be the velocity term. The momentum-based SGD updates for a quadratic loss can be written as:

[math]\displaystyle{ v_{t+1} = \beta\,v_t + \eta\,H\,\theta_t, \quad \theta_{t+1} = \theta_t - v_{t+1}, }[/math]

where [math]\displaystyle{ \beta }[/math] is the momentum coefficient and [math]\displaystyle{ \eta }[/math] is the learning rate.

In the eigenbasis of [math]\displaystyle{ H }[/math], let [math]\displaystyle{ \lambda_i }[/math] be an eigenvalue and [math]\displaystyle{ u_i }[/math] the corresponding eigenvector.

Projecting the iteration onto the direction [math]\displaystyle{ u_i }[/math] yields a scalar recurrence of the form:

[math]\displaystyle{ \theta_{t+1}^{(i)} \;=\; \theta_t^{(i)} \;-\; \bigl[\beta\,v_t^{(i)} \;+\;\eta\,\lambda_i\,\theta_t^{(i)}\bigr]. }[/math]

Because [math]\displaystyle{ v_t^{(i)} }[/math] itself depends on past gradients, the combined effect of [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \eta,\lambda_i }[/math] modifies the “effective” eigenvalue seen in that direction. Specifically:

Small [math]\displaystyle{ \lambda_i }[/math] (Flat Directions)

When [math]\displaystyle{ \lambda_i }[/math] is small, repeated gradient directions are reinforced by [math]\displaystyle{ \beta }[/math], accelerating convergence compared to vanilla SGD. Effectively, momentum increases the update step in directions that change slowly.

Large [math]\displaystyle{ \lambda_i }[/math] (Steep Directions)

If [math]\displaystyle{ \lambda_i }[/math] is large, the term [math]\displaystyle{ \beta,v_t^{(i)} }[/math] moderates the sudden jumps, helping to avoid overshooting. The velocity “remembers” past updates, dampening abrupt swings caused by steep curvature.

Overall, momentum alters the eigenvalues of [math]\displaystyle{ H }[/math] into a more favorable spectrum, reducing the effective condition number. In practice, this translates into faster convergence along flat directions and controlled progress in steep directions, both of which are crucial in the highly non-convex landscapes typical of deep neural networks.

Exercise 4.1

Level: * (Easy)

Exercise Types: Novel

Question

Explain why SURE is rarely used in large-scale deep learning in practice.

Solution

Note that to compute the model complexity part of the SURE estimator, we have to compute the divergence term:

[math]\displaystyle{ 2\sigma^2 \sum_{i=1}^{n} D_i }[/math]

where

[math]\displaystyle{ D_i=\frac{\partial \hat{f}_i(y)}{\partial y_i} }[/math]

For modern deep learning frameworks, both the number of parameters (weights) and the number of data dimensions are huge (in million or billions). This makes the computation of the divergence term extremely expensive. Note that using stochastic gradient descent the estimation of the weights is the result of an iterative process. If we include an inner loop to compute all the divergence, the computation complexity is growing exponentially.

Additionally, the high-dimensional nature of deep learning models means that computing the divergence requires handling large matrices or tensors, making the task even more resource-intensive. Even though parallel computation techniques like GPU acceleration can reduce the time for individual gradient calculations, the divergence computation still adds significant overhead when applied across all data points and iterations. Moreover, the computational complexity becomes even more challenging when dealing with large-scale datasets and real-time training, where the time needed to calculate divergence can slow down the training process substantially. This makes methods like SURE impractical for real-time or large-scale applications compared to simpler and more efficient alternatives like cross-validation, which does not require computing high-dimensional divergence and is easy to implement, making it a more suitable approach in practice.

However, SURE gives very good insight about the behaviour of the true error, and the divergence term is considered a regularization term. For simpler models such as linear regression, the divergence term can be easy to compute, and perturbing a trained data point would not change the estimated function by much. However in more complex models such as deep learning frameworks, perturbing a trained data point can result in large changes in our estimated function, meaning that the divergence term will be larger. Often times, we add a regularization term to our loss function that mimics the behaviour of the divergence term, such that the loss function increases the more complex our model is. Techniques such as adding weight decay or penalties on gradient magnitudes are often used to improve generalization.

Exercise 4.2

Level: * (Easy)

Exercise Types: Novel

Question

Use SURE to analyze how the bias-variance tradeoff is reflected in the risk of an estimator. Consider two scenarios:

• A high-bias, low-variance estimator (e.g., a constant estimate [math]\displaystyle{ \hat{f}(y) = c }[/math] for all [math]\displaystyle{ y }[/math]).
• A high-variance, low-bias estimator (e.g., [math]\displaystyle{ \hat{f}(y) = y }[/math]).
• For the estimator defined by the equation:

[math]\displaystyle{ \hat{f}(y) = cy + d }[/math],

where c and d are constants:

a. Derive the divergence [math]\displaystyle{ \text{D}(\hat{f}). }[/math],

b. Use the derived divergence to compute the SURE formula for the risk.

Show how the SURE formula quantifies the risk in both cases.

Solution

High-bias, low-variance estimator:

• Since [math]\displaystyle{ \hat{f}(y) = c }[/math], the divergence [math]\displaystyle{ \text{D}(\hat{f}) = 0 }[/math] (no dependence on [math]\displaystyle{ y }[/math]).
• The SURE risk simplifies to [math]\displaystyle{ \text{Risk} = (c - y)^2 + 2\sigma^2 \cdot 0 }[/math].
• The expected risk is influenced entirely by the choice of [math]\displaystyle{ c }[/math] relative to [math]\displaystyle{ f }[/math] (bias).

High-variance, low-bias estimator:

• For [math]\displaystyle{ \hat{f}(y) = y }[/math], the divergence [math]\displaystyle{ \text{D}(\hat{f}) = 1 }[/math] (derivative of [math]\displaystyle{ y }[/math] w.r.t. itself is 1).
• The SURE risk becomes [math]\displaystyle{ \text{Risk} = |y - y|^2 + 2\sigma^2 \cdot 1 = 2\sigma^2 }[/math].
• The risk reflects only the variance, as bias is negligible.

Divergence and SURE formula: a. The divergence is [math]\displaystyle{ \text{D}(\hat{f}) = c }[/math] because the derivative of cy + d with respect to y is c.

b. The SURE formula for the risk becomes:

[math]\displaystyle{ \text{Risk} = \mathbb{E}\left[(cy + d - y)^2\right] + 2\sigma^2 \cdot c = \mathbb{E}\left[(c - 1)^2 y^2 + 2(c - 1)d y + d^2\right] + 2\sigma^2 \cdot c }[/math].

Exercise 4.3

Level: ** (Moderate)

Exercise Types: Novel

Question

How does SURE explain why cross-validation and regularization are effective for estimating true error?
Hint: Consider the cases when a data point is not in the training set and when it is included in the training set.

Solution

Let’s first recall the SURE (Stein's Unbiased Risk Estimate) formula:

[math]\displaystyle{ E[(\hat{y_0}-y_0)^2] = E[(\hat{f_0} - f_0)^2] + E[\epsilon_0^2] - 2 E[\epsilon_0 (\hat{f_0} - f_0)] }[/math]

Case 1: Data Point Not in the Training Set

When the data point is not in the training set, the covariance term [math]\displaystyle{ E[\epsilon_0 (f_0 - f_0)] }[/math] becomes zero, since the model does not have access to that particular point during training. This simplifies the formula to:

[math]\displaystyle{ E[(\hat{y_0}-y_0)^2] = E[(\hat{f_0} - f_0)^2] + E[\epsilon_0^2] }[/math]

Now, when summing over all [math]\displaystyle{ m }[/math] points, we obtain:

[math]\displaystyle{ \sum_{i=1}^{m} (\hat{y_i} - y_i)^2 = \sum_{i=1}^{m} (\hat{f_i} - f_i)^2 + m \sigma^2 }[/math]

Where [math]\displaystyle{ \sigma^2 }[/math] is noise. The total error ([math]\displaystyle{ Err }[/math]) can be written as:

[math]\displaystyle{ Err = err - m \sigma^2 }[/math]

Here, [math]\displaystyle{ m \sigma^2 }[/math] is a constant, which means the true error differs from the empirical error by a constant value only. Therefore, the empirical error ([math]\displaystyle{ err }[/math]) provides a good estimate of the true error ([math]\displaystyle{ Err }[/math]) when the point is not in the training set.

This explains why cross-validation is effective. Cross-validation essentially evaluates the model on data points that were not part of the training set, and since the empirical error is only offset by a constant, it provides a reliable estimate of the true error.

Case 2: Data Point in the Training Set

When the data point is part of the training set, the covariance term [math]\displaystyle{ E[\epsilon_0 (f_0 - f_0)] }[/math] is no longer zero. We have:

[math]\displaystyle{ \sum_{i=1}^{m} (\hat{y_i} - y_i)^2 = \sum_{i=1}^{n} (\hat{f_i} - f_i)^2 + n \sigma^2 - 2 \sigma^2 \sum_{i=1}^{n} D_i }[/math]

Where [math]\displaystyle{ D_i }[/math] represents the bias introduced by the model. This equation can be further simplified to:

[math]\displaystyle{ Err = err - n \sigma^2 + 2 \sigma \sum_{i=1}^{n} D_i }[/math]

In this case, the additional term [math]\displaystyle{ \sum_{i=1}^{n} D_i }[/math] reflects the model’s complexity. The complexity term increases with the capacity of the model and is often difficult to calculate directly. To handle this, instead of directly calculating the complexity term, we can use a function that increases with respect to model capacity, and treat it as the regularization term. The regularization term penalizes model complexity to avoid overfitting, thus helping to prevent the model from fitting noise in the training set.

This explains the need for regularization techniques. Regularization helps to control model complexity and ensures that the model generalizes better to unseen data, improving the estimation of the true error.

Thus, both cross-validation and regularization are grounded in the same principle of improving the estimation of true error by adjusting for complexity and noise.

(Note: the formulas are all from Lecture 4 content, STAT 940)

Exercise 4.4

Level: ** (Moderate)

Exercise Types: Novel

Question

Assume there is a point set [math]\displaystyle{ (x_i,y_i) }[/math] satisfying [math]\displaystyle{ y_i=2x_i+3sin(x_i)+n_i }[/math], where [math]\displaystyle{ n_is }[/math] are i.i.d Gaussian with 0 mean and variance of 4.
Now we fit the relationship between y and x, using polynomial linear models with order from 1 to 10. Show the MSE of models of different complexity.

Solution

library(ggplot2)
x <- seq(0, 10, length.out = 100)
y <- 2 * x + 3 * sin(x) + rnorm(100, mean = 0, sd = 2)
data <- data.frame(x = x, y = y)

degrees <- 1:10
mse_values <- numeric(length(degrees))

for (i in seq_along(degrees)) {
  degree <- degrees[i]
  
  model <- lm(y ~ poly(x, degree), data = data)

  predicted <- predict(model, data)
  
  mse_values[i] <- mean((data$y - predicted)^2)
}

mse_results <- data.frame(Degree = degrees, MSE = mse_values)
print(mse_results)

ggplot(mse_results, aes(x = Degree, y = MSE)) +
  geom_line(color = "blue") +
  geom_point(size = 3, color = "red") +
  labs(title = "MSE vs. Model Complexity",
       x = "Polynomial Degree",
       y = "Mean Squared Error (MSE)") +
  theme_minimal()

ggplot(data, aes(x = x, y = y)) +
  geom_point(color = "black", alpha = 0.6) +
  geom_smooth(method = "lm", formula = y ~ poly(x, 1), color = "red", se = FALSE) +
  geom_smooth(method = "lm", formula = y ~ poly(x, 3), color = "blue", se = FALSE) +
  geom_smooth(method = "lm", formula = y ~ poly(x, 10), color = "green", se = FALSE) +
  labs(title = "Polynomial Regression Fits",
       x = "x",
       y = "y") +
  theme_minimal()

Output:

Additional Comment: This graph clearly shows the importance in choosing a good space for your model candidates. When allowing your model to have too much complexity, we see that there is not a lot of reduction in the MSE after 4 polynomial degrees. But there is a big difference from 3 to 4, so based on the graph, it would be best to pick the polynomial of degree 4 as the model as it performed good on the testing dataset while being more robust than models of higher polynomial order.

Exercise 4.5

Level: ** (Easy)

Exercise Types: Novel

Question

Use the SURE equation to explain the difference of using data in the training dataset vs outside of the training dataset in estimating the true error using emperical error (of same size of dataset).

Answer

The Key is in the term [math]\displaystyle{ 2 \sigma^2 \sum_{i=1}^{n} D_i }[/math]. There are overall 2 main terms that contributes to this value ---the number of samples and the variance of the error. If the variance is sufficiently small and the sammple is not too large, the difference between using training datapoints vs testing datapoints would not be as significant. So if the complexity of the model is not very high (low [math]\displaystyle{ D_i }[/math]) with low sample size, using the training dataset to estimate true error will not be extremely different from using a separate dataset.

Exercise 4.6

Level: * (Easy)

Exercise Types: Novel

Question

For a momentum factor [math]\displaystyle{ \beta }[/math], explain the impact of increasing or decreasing [math]\displaystyle{ \beta }[/math] (e.g., [math]\displaystyle{ \beta = 0.9 }[/math] vs. [math]\displaystyle{ \beta = 0.5 }[/math]) on the learning process.

Solution

The momentum factor [math]\displaystyle{ \beta }[/math] determines how much of the velocity contributes to the current step during gradient descent.

When [math]\displaystyle{ \beta }[/math] is high (e.g., [math]\displaystyle{ \beta = 0.9 }[/math]), momentum retains most of the previous velocity, resulting in smoother and more consistent updates. In situations where gradients do not change direction significantly, high [math]\displaystyle{ \beta }[/math] accelerates convergence as momentum accumulates in the correct direction. However, on highly non-convex surfaces or steep gradients, high [math]\displaystyle{ \beta }[/math] may cause oscillations or overshooting as the momentum term dominates gradient changes.

When [math]\displaystyle{ \beta }[/math] is low (e.g., [math]\displaystyle{ \beta = 0.5 }[/math]), the updates rely more heavily on the current gradient rather than accumulated momentum, which can introduce more noise into the updates. In flat regions or long valleys, low [math]\displaystyle{ \beta }[/math] leads to slower progress as previous updates fade quickly. However, a lower [math]\displaystyle{ \beta }[/math] adapts better to situations where the loss landscape changes direction frequently, reducing the risk of overshooting.

Exercise 4.7

Level: ** (Moderate)

Exercise Types: Novel

Question

Suppose we have a linear regression model [math]\displaystyle{ y = X \beta + \varepsilon }[/math] with [math]\displaystyle{ \varepsilon \sim \mathcal{N}\bigl(0, \sigma^2 I\bigr) }[/math]. We use a ridge estimator with penalty [math]\displaystyle{ \lambda }[/math]:

[math]\displaystyle{ \hat{\beta}_\lambda = \bigl(X^\top X + \lambda I\bigr)^{-1} X^\top y, \quad \hat{y}_\lambda = X\,\hat{\beta}_\lambda. }[/math] Write down the form of Stein’s Unbiased Risk Estimator (SURE) for this ridge estimator in terms of [math]\displaystyle{ \hat{y}_\lambda }[/math] and the hat matrix. Briefly explain why the term involving the trace of the hat matrix [math]\displaystyle{ H_\lambda }[/math] adjusts for overfitting, and how that adjustment depends on [math]\displaystyle{ \lambda }[/math]. Describe how you would use SURE to select an optimal value of [math]\displaystyle{ \lambda }[/math].

Solution

1. SURE for the Ridge Estimator Define the hat matrix for ridge regression as:

[math]\displaystyle{ H_\lambda = X \bigl(X^\top X + \lambda I\bigr)^{-1} X^\top, \quad \hat{y}_\lambda = H_\lambda\,y. }[/math] Stein’s Unbiased Risk Estimator (SURE) for this setting is:

[math]\displaystyle{ \mathrm{SURE}(\lambda) = \|y - \hat{y}_\lambda\|^2 + 2\,\sigma^2 \,\mathrm{trace}\bigl(H_\lambda\bigr). }[/math] Here, [math]\displaystyle{ |y - \hat{y}\lambda|^2 }[/math] represents the (in-sample) residual sum of squares, and [math]\displaystyle{ \mathrm{trace}(H\lambda) }[/math] measures the effective degrees of freedom used by the ridge estimator.

2. Role of the Hat Matrix Trace

The matrix [math]\displaystyle{ H_\lambda }[/math] maps the observed data [math]\displaystyle{ y }[/math] to the fitted values [math]\displaystyle{ \hat{y}\lambda }[/math]. Its trace, [math]\displaystyle{ \mathrm{trace}(H\lambda) }[/math], indicates how sensitive the fitted values are to the observed data. Larger [math]\displaystyle{ \mathrm{trace}(H_\lambda) }[/math] means the model is using more degrees of freedom and risks overfitting, causing the naive residual sum of squares [math]\displaystyle{ |y - \hat{y}_\lambda|^2 }[/math] to underestimate true prediction error. As [math]\displaystyle{ \lambda }[/math] increases, the estimator shrinks coefficients more aggressively and [math]\displaystyle{ \mathrm{trace}(H_\lambda) }[/math] typically decreases, reflecting a simpler (less flexible) model. 3. Using SURE to Select [math]\displaystyle{ \lambda }[/math] To choose an optimal [math]\displaystyle{ \lambda }[/math] from the perspective of unbiased risk estimation, one can:

Compute [math]\displaystyle{ \mathrm{SURE}(\lambda) }[/math] over a grid of possible [math]\displaystyle{ \lambda }[/math] values. Select the [math]\displaystyle{ \lambda }[/math] that minimizes [math]\displaystyle{ \mathrm{SURE}(\lambda) }[/math]. Because SURE includes the penalty [math]\displaystyle{ 2,\sigma^2,\mathrm{trace}(H_\lambda) }[/math], it corrects for the bias introduced by fitting the same data used in the residual calculation. This makes SURE a more reliable guide to out-of-sample error than just looking at [math]\displaystyle{ |y - \hat{y}_\lambda|^2 }[/math].

Exercise 5.1

Level: * (Easy)

Exercise Type: Novel

Question

1) Which of the following options can be used to regularize an MLP (choose all that apply)?

a) Add noise to data
b) Use full batch gradient descent
c) Add dropout
d) Use early stopping

2) Using Stochastic Gradient Descent with a small minibatch when training an MLP helps with generalization:

a) True
b) False

Solution

1) The correct answers are a), c), and d).
- a) Adding noise to data is a regularization technique that can improve generalization by forcing the model to learn robust patterns.
- c) Dropout randomly deactivates neurons during training, reducing overfitting.
- d) Early stopping prevents overfitting by halting training once the validation error stops improving.

b) is incorrect because using full batch gradient descent does not help regularize the model.

2) The correct answer is a) True.
Using Stochastic Gradient Descent with a small minibatch size introduces noise into the optimization process, which can act as a form of regularization and improve generalization.

Exercise 5.2

Level: * (Easy)

Exercise Type: Novel

Question

Derive the gradient of the loss function with respect to the weights [math]\displaystyle{ \mathbf{w} }[/math] for the following regularized quadratic loss:

[math]\displaystyle{ L(\mathbf{w}) = \frac{1}{2n} \sum_{i=1}^n \left( y_i - \mathbf{w}^T \mathbf{x}_i \right)^2 + \frac{\lambda}{2} \|\mathbf{w}\|^2 }[/math]

where [math]\displaystyle{ \lambda \gt 0 }[/math] is the regularization parameter.

Solution

The gradient of the loss function [math]\displaystyle{ L(\mathbf{w}) }[/math] with respect to [math]\displaystyle{ \mathbf{w} }[/math] can be computed as follows:

[math]\displaystyle{ \nabla_{\mathbf{w}} L(\mathbf{w}) = \nabla_{\mathbf{w}} \left( \frac{1}{2n} \sum_{i=1}^n \left( y_i - \mathbf{w}^T \mathbf{x}_i \right)^2 \right) + \nabla_{\mathbf{w}} \left( \frac{\lambda}{2} \|\mathbf{w}\|^2 \right) }[/math]

For the first term: [math]\displaystyle{ \nabla_{\mathbf{w}} \left( \frac{1}{2n} \sum_{i=1}^n \left( y_i - \mathbf{w}^T \mathbf{x}_i \right)^2 \right) = -\frac{1}{n} \sum_{i=1}^n \left( y_i - \mathbf{w}^T \mathbf{x}_i \right) \mathbf{x}_i }[/math]

For the second term: [math]\displaystyle{ \nabla_{\mathbf{w}} \left( \frac{\lambda}{2} \|\mathbf{w}\|^2 \right) = \lambda \mathbf{w} }[/math]

Combining both terms: [math]\displaystyle{ \nabla_{\mathbf{w}} L(\mathbf{w}) = -\frac{1}{n} \sum_{i=1}^n \left( y_i - \mathbf{w}^T \mathbf{x}_i \right) \mathbf{x}_i + \lambda \mathbf{w} }[/math]

Exercise 5.3

Level: ** (Moderate)

Exercise Types: Novel

Question

What are the mathematical formulas for Ridge Regression and Lasso Regression, including their respective penalty terms? Additionally, write a Python script that visualizes the effect of these regularization techniques on a selected loss function (e.g., Mean Squared Error) for a simple linear regression model. Once you have the graph, interpret the graph by explaining how the shapes show the differences between Lasso and ridge regression.

Solution

Ridge Regression and Lasso Regression are both forms of linear regression with regularization to prevent overfitting.

Ridge regression minimizes the following objective function:

[math]\displaystyle{ \hat{\beta} = \arg\min_{\beta} \sum_{i=1}^{n} (y_i - X_i \beta)^2 + \lambda \sum_{j=1}^{p} \beta_j^2 }[/math]

where:

• [math]\displaystyle{ y_i }[/math] are the target values,
• [math]\displaystyle{ X_i }[/math] represents the input features,
• [math]\displaystyle{ \beta }[/math] are the regression coefficients,
• [math]\displaystyle{ \lambda }[/math] is the regularization parameter controlling the strength of the penalty.

The penalty term [math]\displaystyle{ \lambda \sum_{j=1}^{p} \beta_j^2 }[/math] ensures that coefficients are shrunk towards zero, reducing overfitting but not setting any coefficients exactly to zero.

Lasso regression introduces an L1 penalty term:

[math]\displaystyle{ \hat{\beta} = \arg\min_{\beta} \sum_{i=1}^{n} (y_i - X_i \beta)^2 + \lambda \sum_{j=1}^{p} |\beta_j| }[/math]

where the L1 penalty term [math]\displaystyle{ \lambda \sum_{j=1}^{p} |\beta_j| }[/math] encourages sparsity in the coefficients. Some coefficients will be set exactly to zero, making Lasso useful for feature selection.

visualization

The following Python script visualizes the impact of Ridge and Lasso regularization by plotting the contours of the Mean Squared Error (MSE) loss function along with the constraint regions imposed by Ridge (L2 ball) and Lasso (L1 diamond):

import numpy as np
import matplotlib.pyplot as plt

# Define the loss function
def mse_loss(beta1, beta2):
    return beta1**2 + beta2**2  # Simplified MSE (for visualization)

# Generate grid for visualization
beta1_vals = np.linspace(-2, 2, 100)
beta2_vals = np.linspace(-2, 2, 100)
B1, B2 = np.meshgrid(beta1_vals, beta2_vals)
Loss = mse_loss(B1, B2)

# Plot contours of the loss function
plt.figure(figsize=(10, 6))
contour = plt.contour(B1, B2, Loss, levels=20, cmap='viridis')
plt.colorbar(contour)

# Plot Ridge constraint (L2 ball)
ridge_circle = plt.Circle((0, 0), radius=1.2, color='red', fill=False, linestyle='dashed', label="Ridge Constraint (L2)")

# Plot Lasso constraint (L1 diamond)
lasso_diamond = np.array([[1, 0], [0, 1], [-1, 0], [0, -1], [1, 0]]) * 1.2
plt.plot(lasso_diamond[:, 0], lasso_diamond[:, 1], 'b--', label="Lasso Constraint (L1)")

# Add constraints to the plot
ax = plt.gca()
ax.add_patch(ridge_circle)
plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)

# Labels and legend
plt.xlabel(r'$\beta_1$')
plt.ylabel(r'$\beta_2$')
plt.title("Effect of Ridge and Lasso Regularization on Loss Function")
plt.legend()
plt.grid(True)
plt.show()

Output:

1. Ridge Regression (L2) – Red Circle

   Ridge regression enforces a circular constraint on the coefficients (β1,β2β1​,β2​).
   The solution is found where the contours of the loss function (MSE) first touch this L2 constraint region.
   Since the constraint is smooth (no sharp corners), the coefficients are shrunk gradually towards zero but rarely exactly zero.
   This means Ridge keeps all features in the model but reduces their impact by shrinking their values.

2. Lasso Regression (L1) – Blue Diamond

   Lasso regression imposes a diamond-shaped constraint on the coefficients.
   The sharp corners of the L1 constraint (at the axes) make it more likely that the optimal solution lies exactly on one of these axes.
   This means Lasso sets some coefficients to exactly zero, effectively performing feature selection by eliminating less important variables.
   The reason for this behavior is that the contours of the loss function often first touch the constraint at the corners, leading to sparsity in the solution.

Conclusion

Ridge Regression (L2) shrinks coefficients continuously but keeps all variables. Lasso Regression (L1) forces some coefficients to exactly zero, performing automatic feature selection.

Exercise 5.4

Level: ** (Moderate)

Exercise Types: Novel

Question

Label smoothing modifies the standard one-hot ground truth labels in multi-class classification by assigning a small amount of probability mass to incorrect classes. Suppose we replace each one-hot label [math]\displaystyle{ y }[/math] with a “smoothed” label [math]\displaystyle{ \tilde{y} }[/math] that assigns [math]\displaystyle{ 1 - \alpha }[/math] to the true class and [math]\displaystyle{ \alpha / (C-1) }[/math] to each of the other [math]\displaystyle{ C - 1 }[/math] classes, where [math]\displaystyle{ C }[/math] is the total number of classes and [math]\displaystyle{ \alpha }[/math] is a small constant.

Write the modified cross-entropy loss using [math]\displaystyle{ \tilde{y} }[/math] and a predicted probability vector [math]\displaystyle{ p }[/math]. Explain how this modification helps reduce model overconfidence and potentially improves calibration. Give an example scenario (e.g., large-scale image classification) where label smoothing has been shown to be particularly beneficial.

Solution

Modified Cross-Entropy Loss Standard cross-entropy for one-hot labels [math]\displaystyle{ y }[/math] and predicted probabilities [math]\displaystyle{ p }[/math] is [math]\displaystyle{ -\sum_{c=1}^C y_c \log p_c. }[/math] With label smoothing, each target label becomes [math]\displaystyle{ \tilde{y}_c }[/math]. Hence, the loss is:

[math]\displaystyle{ \ell_{\mathrm{smooth}} = - \sum_{c=1}^C \tilde{y}_c \,\log p_c, \quad \text{where} \quad \tilde{y}_c = \begin{cases} 1 - \alpha, & \text{for the correct class},\\ \frac{\alpha}{C - 1}, & \text{for other classes}. \end{cases} }[/math] Reduction of Overconfidence and Improved Calibration

In a one-hot scheme, the model is strongly penalized if it does not put near-total probability mass on the correct class. Label smoothing distributes a fraction [math]\displaystyle{ \alpha }[/math] of the probability across incorrect classes, preventing the model from becoming overly confident. By avoiding extreme outputs (probabilities close to 0 or 1), the model tends to produce more calibrated predictions, often generalizing better to unseen data. Example Scenario In large-scale image classification (e.g., ImageNet), label smoothing has demonstrated notable gains:

Models converge more smoothly, especially when data is abundant but still noisy in certain classes. Overconfidence is reduced, leading to improved validation accuracy and calibration metrics.

Regularization in Deep Learning

Introduction

Regularization is a fundamental concept in machine learning, particularly in deep learning, where models with a high number of parameters are prone to overfitting. Overfitting occurs when a model learns the noise in the training data rather than the underlying distribution, leading to poor generalization on unseen data. Regularization techniques aim to constrain the model’s capacity, thus preventing overfitting and improving generalization. This chapter will explore various regularization methods in detail, complete with mathematical formulations, intuitive explanations, and practical implementations.

L2 Parameter Regularization (Weight Decay)

Overview

L2 parameter regularization, commonly known as weight decay, is a technique used to prevent overfitting in machine learning models by penalizing large weights. This penalty helps in constraining the model's complexity.

The regularization term is given by:

[math]\displaystyle{ \mathcal{R}(w) = \frac{\lambda}{2} \|w\|_2^2 }[/math]

where:

• [math]\displaystyle{ \lambda }[/math] is the regularization strength (a hyperparameter),
• [math]\displaystyle{ w }[/math] represents the model weights,
• [math]\displaystyle{ \|w\|_2 }[/math] denotes the L2 norm of the weight vector.

Gradient of the Total Objective Function

The gradient of the total objective function, which includes both the loss and the regularization term, is given by:

[math]\displaystyle{ \nabla_w \mathcal{L}_{\text{total}}(w; X, y) = \lambda w + \nabla_w \mathcal{L}(w; X, y) }[/math]

The weight update rule with L2 regularization using gradient descent is:

[math]\displaystyle{ w := w - \eta (\lambda w + \nabla_w \mathcal{L}(w; X, y)) }[/math]

where [math]\displaystyle{ \eta }[/math] is the learning rate.

Quadratic Approximation to the Objective Function

Consider a quadratic approximation to the objective function:

[math]\displaystyle{ \mathcal{L}(w) \approx \mathcal{L}(w^*) + \frac{1}{2} (w - w^*)^\top H (w - w^*) }[/math]

where:

• [math]\displaystyle{ w^* }[/math] is the optimum weight vector,
• [math]\displaystyle{ H }[/math] is the Hessian matrix of second derivatives.

The modified gradient equation becomes:

[math]\displaystyle{ \lambda w + H (w - w^*) = 0 }[/math]

Solving for [math]\displaystyle{ w }[/math], we get:

[math]\displaystyle{ w = (H + \lambda I)^{-1} H w^* }[/math]

where [math]\displaystyle{ I }[/math] is the identity matrix.

Eigenvalue Decomposition

Assume [math]\displaystyle{ H = Q \Lambda Q^\top }[/math] where [math]\displaystyle{ Q }[/math] is the orthogonal matrix of eigenvectors and [math]\displaystyle{ \Lambda }[/math] is the diagonal matrix of eigenvalues.

Then the weight vector can be expressed as:

[math]\displaystyle{ w = Q(\Lambda + \lambda I)^{-1} \Lambda Q^\top w^* }[/math]

The effect of weight decay is to rescale the coefficients of the eigenvectors. The [math]\displaystyle{ i }[/math]-th component is rescaled by a factor of [math]\displaystyle{ \frac{\lambda_i}{\lambda_i + \lambda} }[/math], where [math]\displaystyle{ \lambda_i }[/math] is the [math]\displaystyle{ i }[/math]-th eigenvalue.

• If [math]\displaystyle{ \lambda_i \gt \lambda }[/math], the effect of regularization is relatively small.
• Components with [math]\displaystyle{ \lambda_i \lt \lambda }[/math] will be shrunk to have nearly zero magnitude.

Effective Number of Parameters

Directions along which the parameters contribute significantly to reducing the objective function are preserved. A small eigenvalue of the Hessian indicates that movement in this direction will not significantly increase the gradient.

The effective number of parameters can be defined as:

[math]\displaystyle{ \text{Effective Number of Parameters} = \sum_i \frac{\lambda_i}{\lambda_i + \lambda} }[/math]

As [math]\displaystyle{ \lambda }[/math] increases, the effective number of parameters decreases, which reduces the model's complexity.

(Placeholder for Image) (Include an image illustrating the effect of weight decay on the eigenvalues and the effective number of parameters)

Dataset Augmentation

Overview

Dataset augmentation is a technique used to improve the generalization ability of machine learning models by artificially increasing the size of the training dataset. This is particularly useful when the amount of available data is limited. The idea is to create new, synthetic data by applying various transformations to the original dataset.

• Key Idea: The best way to make a machine learning model generalize better is to train it on more data. When the amount of available data is limited, creating synthetic data (e.g., by applying transformations like rotation, translation, and noise addition) and adding it to the training set can be effective.

• Practical Example: Operations like translating training images a few pixels in each direction can greatly improve generalization. Another approach is to train neural networks with random noise applied to their inputs, which also serves as a form of dataset augmentation. This technique can be applied not only to the input layer but also to hidden layers, effectively performing dataset augmentation at multiple levels of abstraction.

---

Noise Injection

Overview

Noise injection is a regularization strategy that can be applied in two main ways:

1. Adding Noise to the Input: This method can be interpreted as a form of dataset augmentation and also has a direct connection to traditional regularization methods. 2. Adding Noise to the Weights: This method is primarily used in the context of recurrent neural networks and can be viewed as a stochastic implementation of Bayesian inference over the weights.

Mathematical Proof for Injecting Noise at the Input

Consider a regression setting where we have an input-output pair \( (x, y) \) and the goal is to minimize the expected loss function:

[math]\displaystyle{ J = \mathbb{E}_{x, y} \left[(f(x) - y)^2\right] }[/math]

Now, suppose we inject noise into the input \( x \), where the noise \( \epsilon \) is drawn from a distribution with mean zero (e.g., Gaussian noise \( \epsilon \sim \mathcal{N}(0, \sigma^2) \)). The modified objective function with noise-injected inputs becomes:

[math]\displaystyle{ J_{\text{noise}} = \mathbb{E}_{x, y, \epsilon} \left[(f(x + \epsilon) - y)^2\right] }[/math]

To understand the effect of noise injection, we can expand the function \( f(x + \epsilon) \) around \( x \) using a Taylor series:

[math]\displaystyle{ f(x + \epsilon) = f(x) + \epsilon^\top \nabla_x f(x) + \frac{1}{2} \epsilon^\top \nabla_x^2 f(x) \epsilon + \mathcal{O}(\|\epsilon\|^3) }[/math]

Since the expectation of the noise \( \epsilon \) is zero:

[math]\displaystyle{ \mathbb{E}[\epsilon] = 0 }[/math]

and assuming that the noise is isotropic with covariance matrix \( \sigma^2 I \), the expectation of the second-order term becomes:

[math]\displaystyle{ \mathbb{E}[\epsilon \epsilon^\top] = \sigma^2 I }[/math]

Substituting the Taylor expansion into the objective function:

[math]\displaystyle{ J_{\text{noise}} = \mathbb{E}_{x, y} \left[(f(x) - y)^2\right] + \frac{\sigma^2}{2} \mathbb{E}_{x, y} \left[\|\nabla_x f(x)\|^2\right] + \mathcal{O}(\sigma^4) }[/math]

This shows that the objective function with noise injection is equivalent to the original objective function plus a regularization term that penalizes large gradients of the function \( f(x) \). Specifically, the added term [math]\displaystyle{ \frac{\sigma^2}{2} \mathbb{E}_{x, y} \left[\|\nabla_x f(x)\|^2\right] }[/math] reduces the sensitivity of the network's output to small variations in its input.

Key Result:

For small noise variance \( \sigma^2 \), the minimization of the loss function with noise-injected input is equivalent to minimizing the original loss function with an additional regularization term that penalizes large gradients:

[math]\displaystyle{ J_{\text{noise}} \approx J + \frac{\sigma^2}{2} \mathbb{E}_{x, y} \left[\|\nabla_x f(x)\|^2\right] }[/math]

This regularization term effectively reduces the sensitivity of the output with respect to small changes in the input \( x \), which is beneficial in avoiding overfitting.

Connection to Weight Decay:

In linear models, where \( f(x) = w^\top x \), the gradient \( \nabla_x f(x) \) is simply the weight vector \( w \). Therefore, the regularization term becomes:

[math]\displaystyle{ \frac{\sigma^2}{2} \|w\|^2 }[/math]

which is equivalent to L2 regularization or weight decay.

Manifold Tangent Classifier

Overview

The Manifold Tangent Classifier (MTC) is a classification technique that leverages the idea that data often lies on a lower-dimensional manifold within the high-dimensional input space. The key assumption is that examples on the same manifold share the same category, and the classifier should be invariant to local factors of variation that correspond to movements on the manifold.

• Key Idea: The classifier should be invariant to variations along the manifold while being sensitive to changes that move the data off the manifold.

Tangent Propagation Algorithm

One approach to achieve invariance to manifold variations is to use the Tangent-Prop algorithm (Simard et al., 1992). The main idea is to add a penalty to the loss function that encourages the neural network's output to be locally invariant to known factors of variation. This is achieved by requiring the gradient of the output with respect to the input to be orthogonal to the known manifold tangent vectors \( v_i \) at each point \( x \).

The regularization term can be expressed as:

[math]\displaystyle{ \text{Regularizer} = \lambda \sum_{i} \left(\frac{\partial f(x)}{\partial x} \cdot v_i \right)^2 }[/math]

where:

• \( \frac{\partial f(x)}{\partial x} \) is the gradient of the neural network output with respect to the input,
• \( v_i \) are the known tangent vectors of the manifold,
• \( \lambda \) is the regularization strength.

This regularization ensures that the directional derivative of \( f(x) \) in the directions \( v_i \) is small, promoting invariance along the manifold.

Manifold Tangent Classifier (MTC)

A more recent approach, introduced by Rifai et al. (2011), eliminates the need to know the tangent vectors a priori. The Manifold Tangent Classifier automatically learns these tangent vectors during training, making it more flexible and applicable to a wider range of problems.

---

Early Stopping as a Form of Regularization

Overview

Early stopping is one of the most commonly used forms of regularization in deep learning. Instead of running the optimization algorithm until it reaches a local minimum of the training error, early stopping involves monitoring the validation error during training and halting the process when the validation error stops improving.

• Key Idea: During training, whenever the error on the validation set improves, a copy of the model parameters is stored. The training is stopped when the validation error has not improved for a predetermined amount of time, and the best model parameters (those that resulted in the lowest validation error) are returned.

Mathematical Formulation

Assume that \( w \) represents the model weights (ignoring bias parameters). We take a quadratic approximation to the objective function \( J(w) \) around the empirically optimal value of the weights \( w^* \):

[math]\displaystyle{ J(w) \approx J(w^*) + \frac{1}{2} (w - w^*)^\top H (w - w^*) }[/math]

where:

• \( H \) is the Hessian matrix of second derivatives.

The gradient of the objective function is:

[math]\displaystyle{ \nabla_w J(w) = H(w - w^*) }[/math]

During training, the parameter vector is updated according to:

[math]\displaystyle{ w^{(t+1)} = w^{(t)} - \eta \nabla_w J(w^{(t)}) }[/math]

Substituting the expression for the gradient:

[math]\displaystyle{ w^{(t+1)} - w^* = (I - \eta H) (w^{(t)} - w^*) }[/math]

where \( \eta \) is the learning rate. If we assume that the initial weights are zero (i.e., \( w^{(0)} = 0 \)), we can express the weight update after \( t \) iterations as:

[math]\displaystyle{ w^{(t)} - w^* = (I - \eta H)^t (w^{(0)} - w^*) }[/math]

If we perform an eigenvalue decomposition of \( H \), we get:

[math]\displaystyle{ H = Q \Lambda Q^\top }[/math]

where \( Q \) is the orthogonal matrix of eigenvectors, and \( \Lambda \) is the diagonal matrix of eigenvalues. The weight update can then be rewritten as:

[math]\displaystyle{ w^{(t)} - w^* = Q (I - \eta \Lambda)^t Q^\top (w^{(0)} - w^*) }[/math]

Assuming \( w^{(0)} = 0 \) and that \( |1 - \eta \lambda_i| < 1 \) for all eigenvalues \( \lambda_i \), after \( t \) training updates, we have:

[math]\displaystyle{ Q^\top w^{(t)} \approx [I - (1 - \eta \Lambda)^t] Q^\top w^* }[/math]

Taking the logarithm and using the series expansion for \( \log(1 + x) \), it can be shown that the number of training iterations \( t \) plays a role inversely proportional to the L2 regularization parameter \( \lambda \), and the inverse of \( t \) plays the role of the weight decay coefficient.

Key Insight:

This result shows that early stopping can be interpreted as a form of implicit regularization, where the number of training iterations controls the effective complexity of the model.

Early Stopping as a Form of Regularization

Overview

Early stopping is one of the most commonly used forms of regularization in deep learning. Instead of running the optimization algorithm until it reaches a local minimum of the training error, early stopping involves monitoring the validation error during training and halting the process when the validation error stops improving.

• Key Idea: During training, whenever the error on the validation set improves, a copy of the model parameters is stored. The training is stopped when the validation error has not improved for a predetermined amount of time, and the best model parameters (those that resulted in the lowest validation error) are returned.

Mathematical Formulation

Assume that \( w \) represents the model weights (ignoring bias parameters). We take a quadratic approximation to the objective function \( J(w) \) around the empirically optimal value of the weights \( w^* \):

[math]\displaystyle{ J(w) \approx J(w^*) + \frac{1}{2} (w - w^*)^\top H (w - w^*) }[/math]

where:

\( H \) is the Hessian matrix of second derivatives.

The gradient of the objective function is:

[math]\displaystyle{ \nabla_w J(w) = H(w - w^*) }[/math]

During training, the parameter vector is updated according to:

[math]\displaystyle{ w^{(t+1)} = w^{(t)} - \eta \nabla_w J(w^{(t)}) }[/math]

Substituting the expression for the gradient:

[math]\displaystyle{ w^{(t+1)} - w^* = (I - \eta H) (w^{(t)} - w^*) }[/math]

where \( \eta \) is the learning rate. If we assume that the initial weights are zero (i.e., \( w^{(0)} = 0 \)), we can express the weight update after \( t \) iterations as:

[math]\displaystyle{ w^{(t)} - w^* = (I - \eta H)^t (w^{(0)} - w^*) }[/math]

If we perform an eigenvalue decomposition of \( H \), we get:

[math]\displaystyle{ H = Q \Lambda Q^\top }[/math]

where \( Q \) is the orthogonal matrix of eigenvectors, and \( \Lambda \) is the diagonal matrix of eigenvalues. The weight update can then be rewritten as:

[math]\displaystyle{ w^{(t)} - w^* = Q (I - \eta \Lambda)^t Q^\top (w^{(0)} - w^*) }[/math]

Assuming \( w^{(0)} = 0 \) and that \( |1 - \eta \lambda_i| < 1 \) for all eigenvalues \( \lambda_i \), after \( t \) training updates, we have:

[math]\displaystyle{ Q^\top w^{(t)} \approx [I - (1 - \eta \Lambda)^t] Q^\top w^* }[/math]

Taking the logarithm and using the series expansion for \( \log(1 + x) \), it can be shown that the number of training iterations \( t \) plays a role inversely proportional to the L2 regularization parameter \( \lambda \), and the inverse of \( t \) plays the role of the weight decay coefficient.

Key Insight:

This result shows that early stopping can be interpreted as a form of implicit regularization, where the number of training iterations controls the effective complexity of the model.

Label Smoothing

Label smoothing is a technique to prevent a model from becoming over-confident on a specific class by not forcing the model to fit the data exactly. This approach provides more flexibility and generalization abilities.

Suppose the predicted output is [math]\displaystyle{ y = [0, 1, 0] }[/math], then after applying label smoothing, it becomes [math]\displaystyle{ y = [0.033, 0.933, 0.033] }[/math].

The formula for label smoothing is:

[math]\displaystyle{ y_{\text{smooth}} = (1 - a) \cdot y + \frac{a}{k} }[/math]

where:

• [math]\displaystyle{ a }[/math] is the smoothing factor,
• [math]\displaystyle{ y }[/math] is the original label,
• [math]\displaystyle{ k }[/math] is the number of classes.

The reason for using label smoothing:

• Prevents overfitting: By preventing the model from becoming too confident in its predictions, label smoothing reduces the likelihood of overfitting.
• Improves generalization: Label smoothing can help the model generalize better to unseen data, as it discourages overconfidence in training.

Bagging/Ensemble

Bagging (short for bootstrap aggregating) is a machine learning ensemble technique for reducing generalization error by combining several models (Breiman, 1994)

Explanation: Aggregating is to ombine the predictions of each model, often using voting (for classification) or averaging (for regression).

It works by training several different models separately, and then have all of the models vote on the output for test examples. For example, random forest, which is a popular bagging algorithm that builds multiple decision trees on different bootstrap samples of the data and aggregates their predictions.

The reason why bagging works:

• Variance reduction: By training multiple models on different data subsets, bagging reduces the variance of the predictions. This means that it helps models generalize better to new, unseen data.
• Handling overfitting: Bagging is particularly useful for high-variance models (e.g., decision trees) as it helps reduce overfitting.

While bagging is highly useful for traditional machine learning models, it is less commonly used in deep learning because modern neural networks are already highly expressive. Instead, other ensemble methods, such as model ensembling or dropout, are used.

Code Sample:

from sklearn.ensemble import RandomForestClassifier

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

- Load a dataset (Iris dataset for example) data = load_iris()

X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.3, random_state=42)

- Train a random forest classifier (bagging technique)

rf_model = RandomForestClassifier(n_estimators=100, random_state=42)

rf_model.fit(X_train, y_train)

- Make predictions

y_pred = rf_model.predict(X_test)

- Evaluate the model

accuracy = rf_model.score(X_test, y_test)

Dropout

Overview

Dropout is one of the techniques for preventing overfitting in deepneural network which contains a large number of parameters.

The key idea is to randomly drop units from the neural networkduring training.

• During training, dropout samples from number of different “thinned” network.
• At test time, we approximate the effect of averaging the predictions of all these thinned networks

Model

Consider a neural network with [math]\displaystyle{ L }[/math] hidden layers:

• Let [math]\displaystyle{ z^{(l)} }[/math] denote the vector inputs into layer [math]\displaystyle{ l }[/math].
• Let [math]\displaystyle{ y^{(l)} }[/math] denote the vector of outputs from layer [math]\displaystyle{ l }[/math].
• Let [math]\displaystyle{ W^{(l)} }[/math] and [math]\displaystyle{ b^{(l)} }[/math] represent the weights and biases at layer [math]\displaystyle{ l }[/math].

With dropout, the feed-forward operation becomes:

[math]\displaystyle{ r^{(l)} \sim \text{Bernoulli}(p) }[/math]

[math]\displaystyle{ y^{(l)} = r^{(l)} \odot y^{(l)} }[/math]

where [math]\displaystyle{ \odot }[/math] denotes element-wise multiplication.

The feed-forward equation for layer [math]\displaystyle{ l+1 }[/math] becomes:

[math]\displaystyle{ z^{(l+1)} = W^{(l+1)} y^{(l)} + b^{(l+1)} }[/math]

[math]\displaystyle{ y^{(l+1)} = f(z^{(l+1)}) }[/math]

where [math]\displaystyle{ f }[/math] is the activation function.

For any layer [math]\displaystyle{ l }[/math], [math]\displaystyle{ r^{(l)} }[/math] is a vector of independent Bernoulli random variables, each of which has a probability [math]\displaystyle{ p }[/math] of being 1. The vector [math]\displaystyle{ y^{(l)} }[/math] is the input after some hidden units are dropped. The rest of the model remains the same as a regular feed-forward neural network.

Training

Dropout neural network can be trained using stochastic gradient descent. The only difference here is that we only back propagate on eachthinned network. The gradient for each parameter are averaged over the training cases in each mini-batch.

Test Time

Use a single neural net without dropout If a unit is retained with probability p during training, the outgoing weights of that unit are multiplied by p at test time. [math]\displaystyle{ p \cdot w }[/math]

Additional Regularization

L1 norm

L1 norm regularization, also known as Lasso, is a technique that adds a penalty equal to the absolute value of the magnitude of coefficients to the loss function. This encourages sparsity in the learned weights, meaning it forces some of the weights to become exactly zero, effectively selecting important features and reducing model complexity.

Mixup

Mixup is a data augmentation technique that creates new training examples by taking convex combinations of pairs of input data and their labels. By blending images and labels together, the model learns smoother decision boundaries and becomes more robust to adversarial examples and noise.

Cutout

Cutout is a form of data augmentation where random square regions are masked out (set to zero) in input images during training. This forces the model to focus on a broader range of features across the image rather than relying on any single part, leading to better generalization and robustness.

Gradient Clipping

Gradient clipping is a technique used to prevent the gradients from becoming too large during training, which can cause the model to diverge. This is done by capping the gradients at a predefined threshold, ensuring that updates remain stable, especially in models like recurrent neural networks (RNNs) where exploding gradients are a common issue.

DropConnect

DropConnect is a variation of Dropout, but instead of dropping neurons, it randomly drops connections (weights) between neurons during training. This prevents the co-adaptation of neurons while allowing individual neurons to contribute to learning.

Data Augmentation (beyond Mixup and Cutout)

• Random Flips and Rotations: Randomly flipping (either vertical or horizontal) or rotating images during training to make the model invariant to certain transformations.
• Color Jittering: Modifying the brightness, contrast, saturation, and hue of images to make the model more robust to variations in color.
• Random Cropping and Scaling: Randomly cropping and scaling images to force the model to learn from different perspectives and contexts within the data.

For PyTorch augmentation, one can refer https://pytorch.org/vision/stable/transforms.html

Generalization Paradox

• Models with many parameters tend to overfit
• However, deep neural network, despite using many parameters, works well with unseen data (look up the Double Descent Curve), the reason remains unknown

This phenomenon is illustrated by the Double Descent Curve, where after reaching a peak in test error (due to overfitting), the error decreases again with further model complexity. The precise reasons remain uncertain, but hypotheses include implicit regularization from optimization methods like SGD, hierarchical feature learning, and the redundancy offered by overparameterization.

Batch Normalization

Overview

Batch normalization is a technique used to improve the training process of deep neural networks by normalizing the inputs of each layer. Despite the initial intuition for the method being somewhat incorrect, it has proven to be highly effective in practice. Batch normalization speeds up convergence, allows for larger learning rates, and makes the model less sensitive to initialization, resulting in more stable and efficient training.

Batch normalization motivated by internal covariate shift (2015 lofee & Szegedy)

Internal Covariance Shift

Batch normalization was originally proposed as a solution to the internal covariance shift problem, where the distribution of inputs to each layer changes during training. This shift complicates training because the model must constantly adapt to new input distributions.

The transformation of layers can be described as:

[math]\displaystyle{ l = F_2(F_1(u, \theta_1), \theta_2) }[/math]

For a mini-batch of activations [math]\displaystyle{ X = \{x_1, x_2, \dots, x_m\} }[/math] from a specific layer, batch normalization proceeds as follows:

1. Compute the mean: [math]\displaystyle{ \mu_B = \frac{1}{m} \sum_{i=1}^{m} x_i }[/math]

2. Compute the variance: [math]\displaystyle{ \sigma_B^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_B)^2 }[/math]

3. Normalize the activations: [math]\displaystyle{ \hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} }[/math]

4. Scale and shift the normalized activations using learned parameters [math]\displaystyle{ \gamma }[/math] (scale) and [math]\displaystyle{ \beta }[/math] (shift): [math]\displaystyle{ y_i = \gamma \hat{x}_i + \beta }[/math]

where:

• [math]\displaystyle{ x_i }[/math] represents the activations in the mini-batch,
• [math]\displaystyle{ \mu_B }[/math] is the mean of the mini-batch,
• [math]\displaystyle{ \sigma_B^2 }[/math] is the variance of the mini-batch,
• [math]\displaystyle{ \epsilon }[/math] is a small constant added for numerical stability,
• [math]\displaystyle{ \hat{x}_i }[/math] is the normalized activation,
• [math]\displaystyle{ \gamma }[/math] and [math]\displaystyle{ \beta }[/math] are learned parameters for scaling and shifting.

The batch normalization improves validation accuracy by removing the dropout and enables higher learning rate

Batch Normalization

As mentioned earlier, the original intuition behind batch normalization was found to be incorrect after further research. A paper by Santurkar, S., Tsipras, D., Ilyas, A., & Madry, A. (NeurIPS 2019) contradicted the original 2015 paper on BatchNorm by highlighting the following points:

• Batch normalization does not fix covariate shift.
• If we fix covariate shift, it doesn't help.
• lf we intentionally increase lCS, it doesn't harm.
• Batch Norm is not the only possible normalization. There are alternatives.

Instead, they argue that Batch normalization works better due to other factors, particularly related to its effect on the optimization process:

1. Reparameterization of the loss function:

• Improved Lipschitzness: Batch normalization improves the Lipschitz continuity of the loss function, meaning that the loss changes at a smaller rate, and the magnitudes of the gradients are smaller. This makes the gradients of the loss more "Lipschitz."
• Better β-smoothness: The loss exhibits significantly better smoothness, which aids in optimization by preventing large, erratic changes in the gradient.

2. Variation of the loss function: BatchNorm reduces the variability of the value of the loss. Consider the variation of the loss function: [math]\displaystyle{ \mathcal{L}(x + \eta \nabla \mathcal{L}(x)) }[/math] where [math]\displaystyle{ \eta \in [0.05, 0.4] }[/math]. A smaller variability of the loss indicates that the steps taken during training are less likely to cause the loss to increase uncontrollably.

3. Gradient predictiveness: BatchNorm enhances the predictiveness of the gradients, meaning the changes in the loss gradient are more stable and predictable. This can be expressed as: [math]\displaystyle{ || \nabla \mathcal{L}(x) - \nabla \mathcal{L}(x + \eta \nabla \mathcal{L}(x)) || }[/math], where [math]\displaystyle{ \eta \in [0.05, 0.4] }[/math]. A good gradient predictiveness implies that the gradient evaluated at a given point remains relevant over longer distances, which allows for larger step sizes during training.

Alternatives to Batch Norm

Weight Normalization: Weight normalization is a technique where the weights, instead of the activations, are normalized. This method reparameterizes the weight vectors to accelerate the training of deep neural networks.

Tim Salimans and Diederik P. Kingma, "Weight Normalization: A Simple Reparameterization to Accelerate Training of Deep Neural Networks," 2016.

ELU (Exponential Linear Unit) and SELU (Scaled Exponential Linear Unit): ELU and SELU are two proposed activation functions that have a decaying slope instead of a sharp saturation. They can be used as alternatives to BatchNorm by providing smoother, non-linear activation without requiring explicit normalization.

Djork-Arné Clevert, Thomas Unterthiner, and Sepp Hochreiter, "Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)," In International Conference on Learning Representations (ICLR), 2016. Günter Klambauer, Thomas Unterthiner, Andreas Mayr, and Sepp Hochreiter, "Self-Normalizing Neural Networks," ICLR, 2017.

Convolutional Neural Network (CNN)

Introduction

Convolutional networks are simply neural networks that use convolution instead of general matrix multiplication in at least one of their layers. CNN is mainly used for image processing.

Convolution

In ML, convolution means dot product

[math]\displaystyle{ h = \sigma(\langle x, w\rangle+b) }[/math]

• Same x, different w -- multi-layer perception (MLP)
• Different x, same w -- CNN (weight sharing)

From class, the following operation is called convolution

[math]\displaystyle{ s(t) = \int x(a)w(t-a)ds }[/math]

The convolution operation is typically denoted with an asterisk:

[math]\displaystyle{ s(t) = (x \ast w)(t) }[/math]

Discrete Convolution

If we now assume that x and w are defined only on integer t, we can define the discrete convolution:

[math]\displaystyle{ s[t] = (x \ast w)(t) = \sum_{a=-\infty}^{\infty} x[a] \, w[t-a] }[/math]

[math]\displaystyle{ w[t-a] }[/math] represents the sequence [math]\displaystyle{ w[t] }[/math] shifted by [math]\displaystyle{ a }[/math] units.

In practice

We often use convolutions over more than one axis at a time.

[math]\displaystyle{ s[i,j] = (I * K)[i,j] = \sum_m \sum_n I[m,n] K[i-m, j-n] }[/math]

• Input: usually a multidimensional array of data.

• Kernel: usually a multidimensional array of parameters that should be learned.

We assume that these functions are zero everywhere but the finite set of points for which we store the values.

We can implement the infinite summation as a summation over a finite number of array elements.

Convolution and Cross-Correlation

Convolution is commutative:

[math]\displaystyle{ s[i,j] = (I * K)[i,j] = \sum_m \sum_n I[i-m, j-n] K[m, n] }[/math]

Cross-correlation:

[math]\displaystyle{ s[i,j] = (I * K)[i,j] = \sum_m \sum_n I[i+m, j+n] K[m, n] }[/math]

Many machine learning libraries implement cross-correlation but call it convolution. In the context of backpropagation in neural networks, cross-correlation simplifies the computation of gradients with respect to the input and kernel.

Visualization of Cross-Correlation and Convolution with Matlab (https://www.youtube.com/v/Ma0YONjMZLI)

Image to Convolved Feature

• Kernel\filter size: weight [math]\displaystyle{ \times }[/math] height, e.g. 3 [math]\displaystyle{ \times }[/math] 3 in below example
• Stride: how many pixels to move the filter each time
• Padding: add zeros (or any other value) around the boundary of the input

Example

The following image illustrates a 2D convolution operation between an input image and a filter to produce a convolved feature map.

Image (Input): The grid on the left represents a 5[math]\displaystyle{ \times }[/math]5 matrix of pixel values. The orange-highlighted 3[math]\displaystyle{ \times }[/math]3 region is part of the image currently being convolved with the filter.

Convolution Operation: The filter values are applied to the selected region in an element-wise multiplication followed by a summation. The operation is as follows:

[math]\displaystyle{ (1 \times 1) + (1 \times 0) + (1 \times 1) + (0 \times 0) + (1 \times 1) + (1 \times 0) + (0 \times 1) + (0 \times 0) + (1 \times 1) = 4 }[/math]

Convolved Feature Map: The result value [math]\displaystyle{ 4 }[/math], is placed in the corresponding position (top-left) of the convolved feature map on the right.

One Convolution Example

This process is repeated as the filter slides across the entire image. The final feature map is shown below.

Final Feature Map

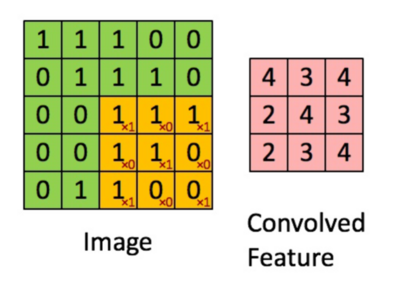
Sparse Interactions

In feed forward neural network every output unit interacts with every input unit.

• When we have [math]\displaystyle{ m }[/math] inputs and [math]\displaystyle{ n }[/math] outputs, then matrix multiplication requires [math]\displaystyle{ (m \times n) }[/math] parameters. and the algorithms used in practice have [math]\displaystyle{ O(m \times n) }[/math] runtime (per example)

Convolutional networks, typically have sparse connectivity (sparse weights). This is accomplished by making the kernel smaller than the input.

• Limit the number of connections each output may have to [math]\displaystyle{ k }[/math], then requires only [math]\displaystyle{ (k \times n) }[/math] parameters and [math]\displaystyle{ O(k \times n) }[/math] runtime

Parameter Sharing

• In a traditional neural net, each element of the weight matrix is multiplied by one element of the input. i.e. It is used once when computing the output of a layer.
• In CNNs, each member of the kernel is used at every position of the input
• Instead of learning a separate set of parameters for every location, we learn only one set

Equivariance

A function [math]\displaystyle{ f(x) }[/math] is equivaraint to a function [math]\displaystyle{ g }[/math] is the following holds:

[math]\displaystyle{ f(g(x)) = g(f(x)) }[/math]

In simple terms: Applying the function [math]\displaystyle{ f }[/math] after [math]\displaystyle{ g }[/math] is equivalent to applying [math]\displaystyle{ g }[/math] after [math]\displaystyle{ f }[/math]

Equivariance

Equivariance in CNNs

• CNNs are naturally equivariant to translation (Covlution = Shift)
• If an input image is shifted, the output feature map shifts correspondingly, preserving spatial structure
• Importance: This property ensures that CNNs can detect features like edges or corners, no matter where they appear in the image

A convolutional layer has equivariance to translation. For example,

[math]\displaystyle{ g(x)[i] = x[i-1] }[/math]

If we apply this transformation to x, then apply convolution, the result will be the same as if we applied convolution to x, then applied the transformation to the output.

For images, convolution creates a 2-D map of where certain features appear in the input. Note that convolution is not equivariant to some other transformations, such as changes in the scale (rescaling) or rotation of an image.

Importance of Data Augmentation

Data augmentation is commonly used to make CNNs robust against variations in scale, rotation, or other transformations. This involves artificially modifying the training data by applying transformations like flipping, scaling, and rotating to expose the network to different variations of the same object.

Convolutional Networks

The first stage (Convolution): The layer performs several convolutions in parallel to produce a set of preactivations. The convolution stage is designed to detect local features in the input image, such as edges and patterns. It does this by applying filters/kernels across the input image.

The second stage (Detector): Each preactivation is run through a nonlinear activation function (e.g. rectified linear). This stage introduces nonlinearity into the model, enabling it to learn complex patterns. Without this nonlinearity, the model would be limited to learning only linear relationships.

The third stage (Pooling) Pooling reduces the spatial dimensions of the feature maps (height and width), helping to make the model more invariant to small translations and distortions in the input image. It also reduces computational load and helps prevent overfitting.

CNN Structure

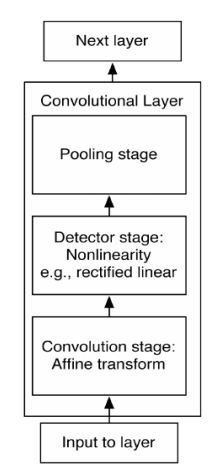
Pooling

Down-sample input size to reduce computation and memory

Popular Pooling functions

• The maximum of a rectangular neighborhood (Max pooling operation)
• The average of a rectangular neighborhood
• The L2 norm of a rectangular neighborhood
• A weighted average based on the distance from the central pixel

Pooling with Downsampling

Max-pooling with a pool width of 3 and a stride between pools of 2. This reduces the representation size by a factor of 2, which reduces the the computational and statistical burden on the next layer.

Pooling and Translations

Pooling helps to make the representation become invariant to small translations of the input. Invariance to local translation can be a very useful property if we care more about whether some feature is present than exactly where it is. For example: In a face, we need not know the exact location of the eyes.

Input of Varying Size

Example: we want to classify images of variable size.

The input to the classification layer must have a fixed size. In the final pooling output (for example) four sets of summary statistics, one for each quadrant of an image, regardless of the image size. Feature after pooling is [math]\displaystyle{ 2 \times 2 }[/math].

It is also possible to dynamically pool features together, for example, by running a clustering algorithm on the locations of interesting features (Boureau et al., 2011).

i.e. a different set of pooling regions for each image.

Learn a single pooling structure that is then applied to all images (Jia et al., 2012)

Convolution and Pooling as an Infinitely Strong Prior

• Weak Prior: a prior distribution that has high entropy, which means there is a high level of uncertainty or spread in the distribution. An example of this would be a Gaussian distribution with high variance
• Strong Prior: has very low entropy, which implies a high level of certainty or concentration in the distribution. An example of this would be a Gaussian distribution with low variance
• Infinitely Strong Prior: places zero probability on some parameters and says a convolutional net is similar to a fully connected net with an infinitely strong prior over its weights

The weights for one hidden unit must be identical to the weights of its neighbor, but shifted in space. The weights must be zero, except for in the small, spatially contiguous receptive field assigned to that hidden unit.

Use of convolution as infinitely strong prior probability distribution over the parameters of a layer. This prior says that the function the layer should learn contains only local interactions and is equivariantto translation.

The use of pooling is infinitely strong prior that each unit should be invariant to small translations. Convolution and pooling can cause underfitting.

Practical Issues

The input is usually not just a grid of real values. It is a grid of vector-valued observations. For example, a color image has a red, green, and blue intensity at each pixel.

When working with images, we usually think of the input and output of the convolution as 3-D tensors. One index into the different channels and two indices into the coordinates of each channel.

Software implementations usually work in batch mode, so they will actually use 4-D tensors, with the fourth axis indexing different examples in the batch.

Training

Suppose we want to train a convolutional network that incorporates convolution of kernel stack [math]\displaystyle{ K }[/math] applied to multi-channel image [math]\displaystyle{ V }[/math] with stride [math]\displaystyle{ s }[/math]:[math]\displaystyle{ c(K; V; s) }[/math]

Suppose we want to minimize some loss function [math]\displaystyle{ J(V; K) }[/math]. During forward propagation, we will need to use [math]\displaystyle{ c }[/math] itself to output [math]\displaystyle{ Z }[/math].

[math]\displaystyle{ Z }[/math] is propagated through the rest of the network and used to compute [math]\displaystyle{ J }[/math].

• During backpropagation, we receive a tensor [math]\displaystyle{ \mathbf{G} }[/math] such that:

[math]\displaystyle{ G_{i,j,k} = \frac{\partial}{\partial Z_{i,j,k}} J(V, K) }[/math]

• To train the network, we compute the derivatives with respect to the weights in the kernel:

[math]\displaystyle{ g(\mathbf{G}, \mathbf{V}, s)_{i,j,k,l} = \frac{\partial}{\partial Z_{i,j,k}} J(V, K) = \sum_{m,n} G_{i,m,n} V_{j,ms+k,ns+l} }[/math]

• If this layer is not the bottom layer of the network, we compute the gradient with respect to [math]\displaystyle{ \mathbf{V} }[/math] to backpropagate the error further:

[math]\displaystyle{ h(\mathbf{K}, \mathbf{G}, s)_{i,j,k} = \frac{\partial}{\partial V_{i,j,k}} J(V, K) = \sum_{l,m \lvert s l + m = j} \sum_{n,p \lvert s n + p = k} \sum_{q} K_{q,i,m,p} G_{i,l,n} }[/math]

Random or Unsupervised Features

The most computationally expensive part of training a convolutional network is learning the features.

• Supervised training with gradient descent requires full forward and backward propagation through the entire network for every gradient update.
• One approach to reduce this cost is to use features that are not learned in a supervised manner, such as random or unsupervised features.

Random Initilizations

Simply initialize the convolution kernels randomly. In high-dimension space, random vectors are almost orthogonal to each other (correlated). Features captured by different kernels are independent.

Unsupervised Learning

Learn the convolution kernels using an unsupervised criterion.

Key insight

Random filters can perform surprisingly well in convolutional networks.

• Layers composed of convolution followed by pooling naturally become frequency-selective and translation-invariant, even with random weights.

Inexpensive architecture selection

• Evaluate multiple convolutional architectures by training only the last layer.
• Choose the best-performing architecture and then fully train it using a more intensive method.

Residual Networks (ResNet)

Overview

Deeper models are harder to train due to vanishing/exploding gradients and can be worse than shallower networks if not properly trained. There are advanced networks to deal with the degradation problem.

ResNet, short for Residual Networks, was introduced by Kaiming He et al. from Microsoft Research in 2015. It brought a significant breakthrough in deep learning by enabling the training of much deeper networks, addressing the vanishing gradient problem.

ResNet Structure

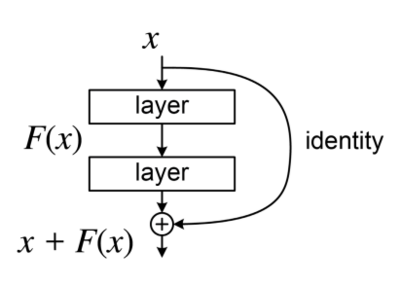
• ResNet introduces the concept of skip connections (or residual connections) that allow the gradient to be directly backpropagated to earlier layers
• Skip connections help in overcoming the degradation problem, where the accuracy saturates and then degrades rapidly as the network depth increases

Variants

Several variants of ResNet have been developed, including ResNet-50, ResNet-101, and ResNet-152, differing in the number of layers.

Application

ResNet has been widely adopted for various computer vision tasks, including image classification, object detection, and facial recognition.

DenseNet

Overview

• DenseNet, short for Densely Connected Networks, was introduced by Gao Huang et al. in 2017.
• It is known for its efficient connectivity between layers, which enhances feature propagation and reduces the number of parameters

DenseNet Structure

Key Feature

The key feature is Dense Connectivity.

• In DenseNet, each layer receives feature maps from all preceding layers and passes its own feature maps to all subsequent layers
• This dense connectivity improves the flow of information and gradients throughout the network, mitigating the vanishing gradient problem

Echo State Network

In RNNs, the ability to capture long-term dependencies is crucial. Set the recurrent and input weights such that the recurrent hidden units do a good job of capturing the history of past inputs, and only learn the output weights. The goal is to access the information from the past implicitly.

The hidden state at time [math]\displaystyle{ t }[/math] can be expressed as:

[math]\displaystyle{ s_t = \sigma(W s_{t-1} + U x_t) }[/math]

where:

• [math]\displaystyle{ W }[/math] represents the recurrent weight matrix, which connects previous hidden states to the current state,
• [math]\displaystyle{ U }[/math] is the input weight matrix, responsible for incorporating the current input [math]\displaystyle{ x_t }[/math],
• [math]\displaystyle{ \sigma }[/math] is an activation function, like a non-linear function such as a sigmoid or tanh.

It is important to control how small changes in the hidden state propagate through time to ensure the network does not become unstable.

If a change [math]\displaystyle{ \Delta s }[/math] in the state at time [math]\displaystyle{ t }[/math] is aligned with an eigenvector [math]\displaystyle{ v }[/math] of the Jacobian [math]\displaystyle{ J }[/math] with eigenvalue [math]\displaystyle{ \lambda \gt 1 }[/math], then the small change [math]\displaystyle{ \Delta s }[/math] becomes [math]\displaystyle{ \lambda \Delta s }[/math] after one-time step, and [math]\displaystyle{ \lambda^t \Delta s }[/math] after [math]\displaystyle{ t }[/math] time steps.

If the largest eigenvalue [math]\displaystyle{ \lambda \lt 1 }[/math], the map from [math]\displaystyle{ t }[/math] to [math]\displaystyle{ t+1 }[/math] is contractive.

The network forgets information about the long-term past.

Set the weights to make the Jacobians slightly contractive. This allows the network to gradually forget irrelevant information while still remembering key long-term dependencies.

Echo State Network

Long Delays

RNNs often fail to capture these dependencies due to the vanishing gradient problem. Long delays use recurrent connections. It knows something from the past, help vanishing gradient - even if gradient get vanished during the path, it still has the direct information from the past.

Long Delays

Leaky Units

In some cases, we do need to forget the path while in some we do not since we do not want to remember redundant information.

Recall that:

[math]\displaystyle{ s_t = \sigma(W s_{t-1} + U x_t) }[/math]

Then consider the following refined form of the equation (convex combination of the current state and previous through a new parameter):

[math]\displaystyle{ s_{t,i} = \left(1 - \frac{1}{\tau_i}\right) s_{t-1} + \frac{1}{\tau_i} \sigma(W s_{t-1} + U x_t) }[/math]

where

• [math]\displaystyle{ 1 \leq \tau_i \leq \infty }[/math]
• [math]\displaystyle{ \tau_i = 1 }[/math] corresponds to an ordinary RNN
• [math]\displaystyle{ \tau_i \gt 1 }[/math] allows gradients to propagate more easily
• [math]\displaystyle{ \tau_i \gg 1 }[/math] means the state changes very slowly, integrating past values associated with the input sequence over a long duration

Infinity means the current state is the previous state while one means completely forgetting the previous steps and only depends on the current observations.

Gated RNNs

Defnition

It might be useful for the neural network to forget the old state in some cases like if we only care about if the current letter is a or b.

Example: [math]\displaystyle{ a\ a\ b\ b\ b\ b\ a\ a\ a\ a\ b\ a\ b }[/math]

It might be useful to keep the memory of the past.

Example:

Instead of manually deciding when to clear the state, we want the neural network to learn to decide when to do it.

Long-Short-Term-Memory (LSTM)

The Long-Short-Term-Memory (LSTM) algorithm was proposed in 1997 (Hochreiter and Schmidhuber, 1997). It is a type of recurrent neural network designed for approaching the vanishing gradient problem.

Several variants of the LSTM are found in the literature:

• Hochreiter and Schmidhuber, 1997
• Graves, 2012
• Graves et al., 2013
• Sutskever et al., 2014

The principle is always to have a linear self-loop through which gradients can flow for a long duration.

Gated Recurrent Units (GRU)

Here is the plain text version of the new image content:

Recent work on gated RNNs, Gated Recurrent Units (GRU), was proposed in 2014.

• Cho et al., 2014
• Chung et al., 2014, 2015
• Jozefowicz et al., 2015
• Chrupala et al., 2015

Standard RNN computes the hidden layer at the next time step directly:

[math]\displaystyle{ s_t = \sigma(W s_{t-1} + U x_t) }[/math]

There are two gates: the update gate and the reset gate. Update gate for the case that we want to keep the information around while reset gate is the case when forgetting. A temporary state locks down some of the values of the current state.

GRU first computes an update gate (another layer) based on the current input vector and hidden state:

[math]\displaystyle{ z_t = \sigma(U^{(z)} x_t + W^{(z)} s_{t-1}) }[/math]

It also computes the reset gate similarly but with different weights:

[math]\displaystyle{ r_t = \sigma(U^{(r)} x_t + W^{(r)} s_{t-1}) }[/math]

New memory content is calculated as:

[math]\displaystyle{ \tilde{s_t} = \tanh(U x_t + r_t \odot W s_{t-1}) }[/math]

which has current observations and forgetting something from the past

If the reset gate is close to 0, this causes the network to ignore the previous hidden state, effectively allowing the model to drop irrelevant information.

The final memory at time step [math]\displaystyle{ t }[/math] is a combination of the current and previous time steps:

[math]\displaystyle{ s_t = z_t \odot s_{t-1} + (1 - z_t) \odot \tilde{s_t} }[/math]

If the reset gate is close to 0, it will ignore the previous hidden state, allowing the model to discard irrelevant information.

The update gate [math]\displaystyle{ z_t }[/math] controls how much of the past state should matter in the current time step. If [math]\displaystyle{ z_t }[/math] is close to 1, then we can effectively copy information from the past state across multiple time steps.

Units that need to capture short-term dependencies often have highly active reset gates.

Cliping Gradients

A simple solution for clipping the gradient. (Mikolov, 2012; Pascanu et al., 2013):

• Clip the parameter gradient from a mini-batch element-wise (Mikolov, 2012) just before the parameter update.
• Clip the norm [math]\displaystyle{ g }[/math] of the gradient [math]\displaystyle{ g }[/math] (Pascanu et al., 2013a) just before the parameter update.

The formula for clipping the gradient is:

[math]\displaystyle{ g' = \min\left(1, \frac{c}{|g|}\right) g }[/math]

where c is a constant.

Attention

The attention mechanism was introduced to improve the performance of the encoder-decoder model for machine translation.

Common Representation

A single 'concept' is universally represented, transcending specific languages or forms.

• Encoder: Processes the word 'elephant' from its original source.
• Output: A universal representation vector (the abstract 'concept' of an elephant).
• Decoders: Translate this concept into various domains or applications.

The 'concept' is an abstract entity that exists independently of any particular language or representation.

For example, if we want to translate from English to Spanish

• Encoder (English Input): The system processes the word "elephant."
• Output (Universal Representation): The system generates an abstract concept or vector representing an "elephant," independent of any specific language.
• Decoder (Spanish Output): The system decodes this concept and outputs the equivalent Spanish word: "elefante."

Common Representation

Sequence-to-Sequence Model

In the sequence-to-sequence model, every word [math]\displaystyle{ x_i }[/math] produces a hidden vector [math]\displaystyle{ h_i }[/math] in the encoder part of the autoencoder. The hidden vector of every word, [math]\displaystyle{ h_i }[/math], is fed to the next hidden vector, [math]\displaystyle{ h_{i+1} }[/math], by a projection matrix [math]\displaystyle{ W }[/math].

In this model, for the whole sequence, there is only one context vector [math]\displaystyle{ c }[/math], which is equal to the last hidden vector of the encoder, i.e., [math]\displaystyle{ c = h_n }[/math].

Sequence-to-Sequence Model

Challenges:

1. Long-range dependencies: As the model processes long sequences, it can struggle to remember and utilize information from earlier steps, especially in cases where long-term context is crucial.

2. Sequential processing: Since these models process data step by step in sequence, they can't take full advantage of parallel processing, which limits the speed and efficiency of training.

These are the core challenges that newer architectures, such as transformers, aim to address.

Attention Definition

The basic idea behind the attention mechanism is directing the focus on important factors when processing data. Attention is a fancy name for weighted average.

Sequence-to-Sequence Model with Attention

• Sequence-to-sequence models:

Multiple RNN units serve as the encoder. They encode information into the context vectors. Multiple RNN units decode the concept in the context vector to different domain information. The limitations of this approach are long-range dependencies and prevention of parallelization.

[math]\displaystyle{ p(y_i | y_1, \ldots, y_{i-1}) = g(y_{i-1}, l_i, c) }[/math]

• Sequence-to-sequence with attention:

Pass multiple context vectors to the decoder.

[math]\displaystyle{ p(y_i | y_1, \ldots, y_{i-1}) = g(y_{i-1}, l_i, c_i) }[/math]

Sequence-to-Sequence Model with Attention

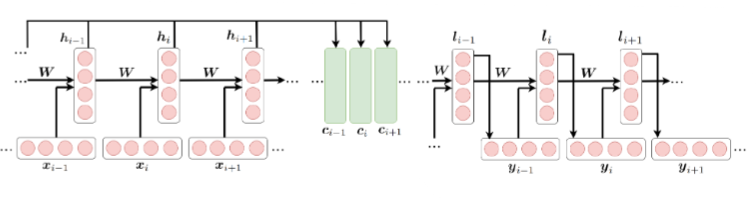
There are some calculations:

1. Similarity score: [math]\displaystyle{ s_{ij} = similarity(l_{i-1}, h_j) }[/math]

2. Attention weight: [math]\displaystyle{ a_{ij} = \frac{e^{s_{ij}}}{\sum_{k=1}^{T} e^{s_{ik}}} }[/math]

The attention weight [math]\displaystyle{ a_{ij} }[/math] is obtained by applying a softmax function to the similarity scores. This normalizes the scores across all encoder hidden states, turning them into a probability distribution.

3. Context vector: [math]\displaystyle{ c_i = \sum_{j=1}^{T} a_{ij} h_j }[/math]

The effectiveness of the correlation between inputs around position [math]\displaystyle{ j }[/math] and the output at position [math]\displaystyle{ i }[/math] is crucial.

This score is determined based on:

• The RNN hidden state [math]\displaystyle{ l_{i-1} }[/math] just before emitting [math]\displaystyle{ y_i }[/math].
• The [math]\displaystyle{ j^{th} }[/math] hidden state [math]\displaystyle{ h_j }[/math] of the input sentence.

Transformer Architecture

The basic concept behind transformers is attention as summarized in the paper by Vaswani et. al 'Attention is all you need'. This paper claims that all you need is attention and with the structure of attentions, basically you can handle the sequential data. It was based on GPT and many other models that we use in LLM and imaging processing. Transformer is an example of an encoder-decoder architecture. Unlike RNNs, Transformers can process sequences in parallel, making them faster to train on large datasets. Transformers have applications beyond NLP, such as Vision Transformers (ViT) in computer vision and protein structure prediction in biology (AlphaFold). Transformers' ability to capture long-range dependencies efficiently has made them the standard for many modern AI models.

Encoder

The encoder consists of two main components: Self Attention and Feed Forward Neural Network. The architecture of the Encoder is given below:

Encoder architecture of the Transformer

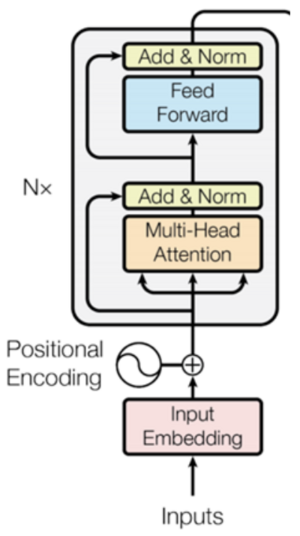
Self Attention

Understanding the individual words in a sentence is not enough to understand the whole sentence and one needs to understand how the words relate to each other. The attention mechanism forms composite representations. We aim to have embeddings of words and embeddings of compositions at the same time in different levels. Unlike word2vec introduced in 2013 by Mikolov et al., which captures the vector representations of words in an embedding space such that words that are similar are represented closer to each other, self-attention aims to capture the similarity between words based on context and in relation to each other. Multiple layers help form complex concept representations. For example, the context of the word "bank" differs based on if the surrounding words involve "money" or "river".

Illustration of word2vec where "King" - "Man" + "Woman" produces a vector close to the word "Queen"

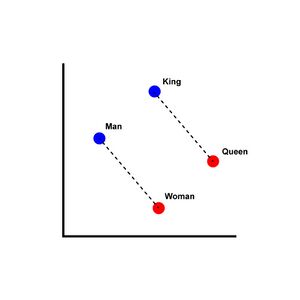
Self-attention is analogous to the fundamental retrieval strategy in databases where given a query, and key-value pairs, we use the query to identify the key and retrieve the corresponding value. The generalized definition for calculating the attention of a target word with respect to the input word: use the Query of the target and the Key of the input and then calculate a matching score. These matching scores act as the weights of the Value vectors.

Then we look at the definition if matrix form. Given an input vector [math]\displaystyle{ \mathbf{x} \in \mathbb{R}^d }[/math], the weights for the query, key, and value transformations are defined as:

• Query weight matrix: [math]\displaystyle{ \mathbf{W}_q \in \mathbb{R}^{d \times p} }[/math]

• Key weight matrix: [math]\displaystyle{ \mathbf{W}_k \in \mathbb{R}^{d \times p} }[/math]

• Value weight matrix: [math]\displaystyle{ \mathbf{W}_v \in \mathbb{R}^{d \times r} }[/math]

The transformations for the query ([math]\displaystyle{ \mathbf{q} }[/math]), key ([math]\displaystyle{ \mathbf{k} }[/math]), and value ([math]\displaystyle{ \mathbf{v} }[/math]) vectors are given by:

• Query vector: [math]\displaystyle{ \mathbf{q} = \mathbf{W}_q^T \mathbf{x} }[/math] where [math]\displaystyle{ \mathbf{q} \in \mathbb{R}^{p \times 1} }[/math], since [math]\displaystyle{ \mathbf{W}_q^T \in \mathbb{R}^{p \times d} }[/math], and [math]\displaystyle{ \mathbf{x} \in \mathbb{R}^{d \times 1} }[/math]

• Key vector: [math]\displaystyle{ \mathbf{k} = \mathbf{W}_k^T \mathbf{x} }[/math] where [math]\displaystyle{ \mathbf{k} \in \mathbb{R}^{p \times 1} }[/math], since [math]\displaystyle{ \mathbf{W}_k^T \in \mathbb{R}^{p \times d} }[/math], and [math]\displaystyle{ \mathbf{x} \in \mathbb{R}^{d \times 1} }[/math]

• Value vector: [math]\displaystyle{ \mathbf{v} = \mathbf{W}_v^T \mathbf{x} }[/math] where [math]\displaystyle{ \mathbf{v} \in \mathbb{R}^{r \times 1} }[/math], since [math]\displaystyle{ \mathbf{W}_v^T \in \mathbb{R}^{r \times d} }[/math], and [math]\displaystyle{ \mathbf{x} \in \mathbb{R}^{d \times 1} }[/math]

The transformations allow the attention mechanism to compute similarity scores between the query and key vectors and to use the value vectors to produce the final weighted output as [math]\displaystyle{ \mathbf{z_1} = \alpha_1 \mathbf{v}_1 + \alpha_2 \mathbf{v}_2 + \ldots + \alpha_n \mathbf{v}_n }[/math], where [math]\displaystyle{ \mathbf{v}_i }[/math] are similar to the input in CNNs, and [math]\displaystyle{ \alpha_i }[/math] are similar to the kernels in CNNs.

However, unlike the kernels in CNNs, the [math]\displaystyle{ \alpha_i }[/math]'s are data-dependent and given by: [math]\displaystyle{ \alpha_i = \text{softmax}\left(\frac{\mathbf{q}^T \mathbf{k}_i}{\sqrt{p}}\right) }[/math].

Extending this to the entire dataset, the equations are:

[math]\displaystyle{ \mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n] \in \mathbb{R}^{d \times n} }[/math]

[math]\displaystyle{ \mathbf{Q} = [\mathbf{q}_1, \mathbf{q}_2, \ldots, \mathbf{q}_n] \in \mathbb{R}^{p \times n} }[/math]

[math]\displaystyle{ \mathbf{K} = [\mathbf{k}_1, \mathbf{k}_2, \ldots, \mathbf{k}_n] \in \mathbb{R}^{p \times n} }[/math]

[math]\displaystyle{ \mathbf{V} = [\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_n] \in \mathbb{R}^{r \times n} }[/math]

The transformations are defined as:

[math]\displaystyle{ \mathbf{Q}_{p \times n} = \mathbf{W}_{q}^{T_{p \times d}} \mathbf{X}_{d \times n} }[/math]

[math]\displaystyle{ \mathbf{K}_{p \times n} = \mathbf{W}_{k}^{T_{p \times d}} \mathbf{X}_{d \times n} }[/math]

[math]\displaystyle{ \mathbf{V}_{r \times n} = \mathbf{W}_{v}^{T_{r \times d}} \mathbf{X}_{d \times n} }[/math]

Therefore the output, [math]\displaystyle{ \mathbf{Z}_{r \times n} = \mathbf{V}_{r \times n} \cdot \text{softmax}\left(\frac{\mathbf{Q}^{T} \mathbf{K}}{\sqrt{p}}\right)_{n \times n} }[/math]

Additionally, we have:

[math]\displaystyle{ \mathbf{Q}^{T} \mathbf{K} = \mathbf{X}^{T} \mathbf{W}_{q} \mathbf{W}_{k}^{T} \mathbf{X} \quad \text{(an asymmetric kernel extracting the global similarity between words)} }[/math]

Let us take a closer look at how one word is processed in the encoder.

Deeper view of the Encoder

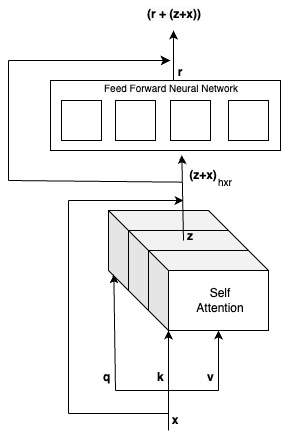
The input vector x is passed through a linear transformation layer which transforms the input into query q, key k, and value v vectors, given by the equations above. This is passed through a stacked multi-head self-attention layer which extracts global information across pairwise sequence of words to produce the output vector Z also given by the equation above. The equation for Z can be compared to how similarity is computed between the key and value pairs in databases. This output is added to the residual input x to preserve the meaning of individual words in addition to the pairwise representations. This is normalized to produce the output [math]\displaystyle{ \mathbf{(Z+x)} \in \mathbb{R}^{h \times r} }[/math]. This serves as the input to the feed forward neural network.

Feed Forward Neural Network

The structure of the feed forward network (FFN) is Linear Layer 1, followed by ReLU activation and then another linear layer 2. While the attention mechanism captures global information between words and hence aggregates across columns, the feed forward neural network aggregates across rows and takes a more broader look at each word independently. Depsite the individual processing, all positions share the same set of weights and biases in the FFN. In a classroom environment, the attention mechanism is similar to the teacher observing the interactions among students in a group, whereas the feed forward neural network resembles the teacher evaluating each student independently for their understanding of the assignment. The output of the feed forward layer r also has a residual connection from the previous layer which is normalized and passed as the input of the decoder as [math]\displaystyle{ \mathbf{(r+(z+x))} }[/math]. The encoder also has a positional encoding component which captures information about the position of words in a sequence.

While the above figure zooms in at how a word vector x is processed by the encoder, the major advantage of the transformer architecture is its ability to handle multiple words in a sequence in parallel and so in practice, the above zoomed in version of the encoder is usually stacked to handle a group of words in parallel.

==== Global v.s. Local Information

For Attention Mechanism:

• Global Understanding: Captures relationships among different positions in the sequence.
• Context Aggregation: Spreads relevant information across the sequence, enabling each position to see a broader context.

For Feed-Forward Networks (FFN):

• Local Processing: While attention looks across the entire sequence, FFN zooms back in to process each position independently.
• Individual Refinement: Enhances the representation of each position based on its own value, refining the local information gathered so far.

Decoder

The decoder consist of three main components: Masked Self Attention, Cross Attention and Linear Layer. The architecture of the Decoder is given below:

Decoder architecture of the Transformer

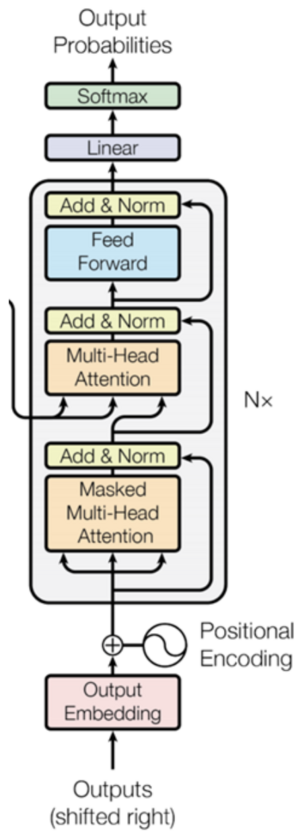
Masked Self Attention

In masked self attention, we add a mask matrix [math]\displaystyle{ \mathbf{M} \in \mathbb{R}^{n \times n} }[/math] to the normalized argument within the softmax of [math]\displaystyle{ \mathbf{Z} }[/math] given by [math]\displaystyle{ \mathbf{Z}_{r \times n} = \mathbf{V}_{r \times n} \cdot \text{softmax}\left(\frac{\mathbf{Q}^{T} \mathbf{K} + \mathbf{M}}{\sqrt{p}}\right)_{n \times n} }[/math] The reason for adding a mask matrix M is to ensure that the output is informed only by the past words and not by the words further along in the sequence. The mask matrix therefore is given by:

[math]\displaystyle{ M(i,j) = \begin{cases} 0 & \text{if } j \leq i \\ -\infty & \text{if } j \gt i \end{cases} }[/math]

This is because [math]\displaystyle{ \mathbf{Z} }[/math] is an upper triangular matrix with values for previous words since [math]\displaystyle{ softmax(x + 0) }[/math] is the same as [math]\displaystyle{ softmax(x) }[/math], but [math]\displaystyle{ softmax(x - \infty) }[/math] will be equal to 0.

Cross Attention

The intuition behind cross attention is similar to sequence-to-sequence models where the context vector is passed from the encoder to the decoder capturing relevant information from the input sequence. The residual connection plus the output of the masked self attention is passed as the query to the cross attention block, whereas the key and value pairs are the same as the output of the encoder. The relationship and relevance between words in different sentences are captured.

Linear Layer

The linear layer is applied to the output of the feed forward neural network of the decoder and its primary role is to adjust the dimensionality of the network to match the size of the vocabulary. It involves learning a set of parameters - a matrix of dimension equal to [math]\displaystyle{ p \times len(vocab) }[/math]. This results in a [math]\displaystyle{ p \times 1 }[/math] vector which is then passed through a probabilistic softmax layer to predict the next word in the sequence.

Softmax Activation

The function transforms the linear layer's output into probabilities as mentioned above. The output represents the likelihood of a respective word being the next word in the sequence.

Positional Encoding

So far, the encoder and decoder has no sense of the order of the words in the sequence. The sentences "I am a teacher", "Teacher I am", "Am I a teacher?" are processed the same way, even though the meaning may not be the same. To circumvent this issue, and due to the lack of the convolution or recurrence operations, a positional encoding scheme is embedded within the encoder and decoder. In this encoding, the position of the words in a sequence is encoded by a vector. The even positions are represented by a sinusoidal wave with 1 representing the peaks and 0 representing the troughs. Similarly, the odd positions are represented by a cosine wave. Thus, each position is encoded by a unique binary vector and each unique binary vector represents a specific position.

Bidirectional Encoder Representations from Transformers (BERT)

BERT introduced by Google is built by repeating the encoder of the transformer multiple times. The Bidirectional in BERT refers to its ability to attend to the future and past words in the sequence unlike Transformers which only looks at the past to make predictions about the future. The fundamental principles behind BERT are Masked Language Modeling, and Next Sentence Prediction. The architecture of BERT is given below.

Masked Language Modeling

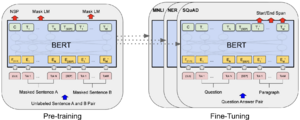
Masked Language Modeling

BERT masks words in a corpus as shown in the figure below and makes the model learn to predict these words. It thereby pays attention to both words before and after the masked word and fills in the blank given the entire context. It is the same as a Transformer Encoder where 12 encoders (in contrast to the 6 in the original paper of Transformers) are stacked on top of each other. The output of the encoder is passed to s linear dense layer and softmax to predict the most probable word from the vocabulary of the corpus.

Masked Language Modeling

Next Sentence Prediction

It was also used to identify if given two sentences A and B, B logically follows the sentence A. This is possible due to the ability to fine-tune the weights of the pretrained BERT model for downstream prediction tasks. The pre-trained model can also be used to represent the input of a sentiment analysis task (for example) to a neural network in a better manner. The [CLS] token is prepended to the input sequence and is used to capture the context of the whole sentence such that during fine-tuning, the prediction may be conditioned on the representation of the [CLS] token.

There are various flavors of BERT based on slight modifications to the original architecture and training processes. The advantage of fine tuning pretrained models is the opportunity to finetune them on a domain specific corpus leading to additional variants of BERT as BioBERT retrained on a biomedical corpus, BERTweet trained on around 850 million tweets and so on.

Transformers and GPT Models

Overview of Transformers

• Transformers consist of two main components:
  • Encoder
  • Decoder
• BERT utilizes a stack of encoders, while GPT uses a stack of decoders.
• GPT models are neural network-based language prediction models built on Transformer architecture.

Decoder Structure

• The decoder has three parts:
  1. Masked Multi-Head Attention: Attends only to the left.
  2. Cross Attention: Attends to encoded inputs (removed in GPT).
  3. Feed Forward Neural Network.

Differences Between BERT and GPT

• Both BERT and GPT use masked multi-head attention, but unlike BERT that masks a word in the middle of the sentence, and tries to predict the mask, GPT masks all the future words and tries to predict them.
• Training methods differ:
  • BERT masks tokens in sentences.
  • GPT predicts the next token in a sequence.

Training Process

• In GPT, the model predicts the next token based on the previous tokens, treating the input as a sequence.
• The first GPT model (2018) had 117 million parameters and was trained on 7,000 books.
• It was seen that larger models tend to generalize better and have better "emergent abilities", although the reason is still unclear.

Evolution of GPT Models

• GPT-2 (2019) had 1.5 billion parameters.
• GPT-3 (2020) had 175 billion parameters.
• Larger models tend to generalize better. This trend suggests that increasing model size allows for deeper contextual understanding.

Chain of Thought Reasoning

• GPT-4 introduced a method called “chain of thought,” allowing the model to predict intermediate steps in reasoning tasks. It involves multi-step thinking: The model generates a series of logical steps to arrive at the final answer, rather than answering in a single sentence.
• Example: Problem: What is the result of 5 + 5 + 5? It is clear to see the answer is 15. With the chain of thought reasoning - Step 1: The first 5 plus the second 5 gives 10 (i.e. [math]\displaystyle{ 5+5=10 }[/math]). Step 2: add the last 5 to the result from Step 1 (i.e. [math]\displaystyle{ 10+5=15 }[/math]).

Alignment and Instruction Following

• ChatGPT is designed to follow instructions and align with user preferences, addressing issues like harmful or politically incorrect outputs.
• InstructGPT is a variant of GPT that focuses on following instructions using human feedback via Reinforcement Learning from Human Feedback (RLHF).

Text-Text Transfer Transformer (T5)

• T5 combines encoder and decoder structures and treats various NLP tasks as text-to-text problems, allowing for diverse applications like translation and summarization.
• NLP tasks such as sentiment analysis which were primarily treated as classification problems are cast as text-to-text problems.
• Next span prediction is used where a set of sequential tokens are removed and replaced with sentinel tokens.
• T5 architecture operates on an encoder-decoder model and encoder input padding can be performed on both left and right.

Training Techniques in T5

• T5 masks spans of tokens rather than individual tokens, focusing on global context rather than local dependencies. 15% of tokens are randomly removed and replaced with sentinel tokens.

Benchmarking and Performance

• Models are often evaluated against benchmarks like GLUE and SuperGLUE, which consist of various NLP tasks.

Training and Fine-Tuning LLMs

• LLMs are trained on massive datasets of unlabeled text using unsupervised learning.
• The training process involves predicting the next token in a sequence.
• Fine-tuning is done on labeled data to align the model with specific tasks or instructions. This process is called Supervised Fine-Tuning (SFT).

Aligning LLMs with Human Feedback

• Reinforcement Learning with Human Feedback (RLHF) is used to ensure LLMs produce safe and ethical outputs.
• RLHF involves generating multiple responses for a given prompt and having humans rank them.
• A reward model is trained on this ranked data to predict the quality of a response.
• The original LLM is then fine-tuned using this reward model.
• RLHF was introduced in 2017 and has been widely used in LLMs like ChatGPT.

Direct Preference Optimization (DPO)

• DPO is a newer approach that aims to replace RLHF.
• It directly collects user preferences for different responses, eliminating the need for a reward model.
• DPO is easier to implement and more stable than RLHF.

Project Ideas for Deep Learning

1. Enhancing Speculative Decoding for Faster Large Language Modeling
   • This project aims to improve the speed of LLMs by using techniques like rejection sampling and importance sampling.
   • The goal is to find alternative sampling methods to rejection sampling, which is computationally expensive.
2. Reducing the Computational Complexity of Transformers
   • Transformers are computationally expensive, especially for long sequences.
   • This project explores methods like ORCID, which uses data-dependent convolution to reduce complexity.
   • The goal is to develop more efficient transformers that can handle longer sequences.
3. Diffusion Decoding for Peptide De Novo Sequencing
   • Peptide sequencing is a crucial problem in bioinformatics, involving determining the amino acid sequence of a peptide.
   • This project proposes using diffusion models for peptide sequencing, replacing the traditional GPT-based approach.
   • Diffusion models can potentially improve accuracy by predicting all tokens simultaneously, rather than sequentially.
4. Using ORCID for DNA Analysis
   • This project explores using ORCID, a model that can handle larger sequences, for DNA analysis.
   • The goal is to leverage ORCID’s ability to handle long sequences to improve DNA analysis tasks.
5. Symbolic Regression with Diffusion Models
   • Symbolic regression involves finding a mathematical formula that best fits a given dataset.
   • This project proposes using diffusion models for symbolic regression, potentially improving the accuracy and efficiency of the process.

Transformers and Variational Autoencoders

Large Language Models (LLMs) and Transformers

Key Components of Transformers

• Attention Mechanism Formula: The core of the attention mechanism is computed using the following formula:

[math]\displaystyle{ V \text{softmax} \left( \frac{Q^T K}{\sqrt{p}} \right) \quad \text{(n x n)} }[/math]

• Dimensions:
  • [math]\displaystyle{ X }[/math] as a [math]\displaystyle{ d \times n }[/math] matrix, [math]\displaystyle{ n }[/math] as sequence length, and [math]\displaystyle{ d }[/math] as data dimensionality.
  • [math]\displaystyle{ Q }[/math], [math]\displaystyle{ K }[/math] and [math]\displaystyle{ V }[/math] are the query, key, and value matrices, respectively, and they are derived from [math]\displaystyle{ W_Q }[/math], [math]\displaystyle{ W_K }[/math] and [math]\displaystyle{ W_V }[/math].
  • Given a sequence [math]\displaystyle{ X = \begin{bmatrix} x_1 & \cdots & x_n \end{bmatrix}_{d \times n} }[/math] we define:
    • [math]\displaystyle{ Q = W_Q^T X \quad \text{(p x n)}, \quad W_Q^T \in \mathbb{R}^{p \times d}, \quad X \in \mathbb{R}^{d \times n} }[/math]
    • [math]\displaystyle{ K = W_K^T X \quad \text{(p x n)}, \quad W_K^T \in \mathbb{R}^{p \times d} }[/math]
    • [math]\displaystyle{ V = W_V^T X \quad \text{(m x n)}, \quad W_V^T \in \mathbb{R}^{m \times d} }[/math]

Recap of Transformers

• Building Blocks of LLMs: Transformers.
• Computational Complexity:
  • Issue: Transformers have quadratic complexity concerning sequence length.
  • Reason: Complexity arises due to calculations in the attention mechanism.

Approaches to Reduce Complexity

• Issue: Long sequences result in an [math]\displaystyle{ n \times n }[/math] matrix, making computation demanding.
• Solution: Techniques like the Performer model approximate attention, reducing complexity to linear time.

Performer Model

Overview

• Objective: Address quadratic complexity in transformers by approximating attention using kernel methods.
• Kernel Approximation: Utilizes random features to approximate kernels, e.g., Gaussian kernels. The kernel function [math]\displaystyle{ K(x, y) }[/math] is defined as:

[math]\displaystyle{ K_{\text{Gauss}}(x, y) = \varphi(x)^T \varphi(y) }[/math]

• For the Gaussian kernel approximation, the transformation [math]\displaystyle{ \varphi_{\text{Gauss}}(x) }[/math] is given by:

[math]\displaystyle{ \varphi_{\text{Gauss}}(x) = \frac{1}{\sqrt{r}}\begin{pmatrix} \sin(\omega_1^T x), & \sin(\omega_2^T x), & \dots, & \sin(\omega_r^T x), \cos(\omega_1^T x), & \cos(\omega_2^T x), & \dots, & \cos(\omega_r^T x)\end{pmatrix} }[/math]

• In general for kernel [math]\displaystyle{ K }[/math]:

[math]\displaystyle{ \phi(x) = \frac{h(x)}{\sqrt{ r }}(f_{1}(w_{1}^Tx) \dots f_{1}(w_{r}^Tx) \dots f_{l}(w_{1}^Tx) \dots f_{l}(w_{r}^Tx)) \quad \text{(l x r)} }[/math]

Advantage

Scalability: Performers are highly scalable for very long sequences.

Memory Efficiency: Performers drastically reduce memory usage by linearizing attention.

Robust Performance: Despite the approximation, Performers retain high accuracy and performance, comparable to standard transformers.

Application

Performers are beneficial in applications requiring efficient processing of long sequences, such as natural language processing, DNA sequence analysis, and other domains where traditional transformers are computationally prohibitive.

Softmax and Attention Mechanism in Transformers

Softmax Formula

• In the context of transformers, the softmax function is used to normalize the attention scores:

[math]\displaystyle{ \text{SM}[s]_i = \frac{e^{s_i}}{\sum_j e^{s_j}} }[/math]

• To calculate the softmax numerically, we can consider:

[math]\displaystyle{ e^{Q^T K} = A }[/math]

[math]\displaystyle{ d = \begin{bmatrix} & & & & \\ & & & & \\ & & & & \end{bmatrix}_{n \times n} \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix}_{n \times 1} \\ }[/math]

[math]\displaystyle{ D = \operatorname{diag}(d) = \begin{bmatrix} d_1 & 0 & \cdots & 0 \\ 0 & d_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & d_n \end{bmatrix}_{n \times n} }[/math]

[math]\displaystyle{ \operatorname{SM}[s]_i = \frac{e^{s_i}}{\sum_j e^{s_j}} = A D^{-1} }[/math]

• We want to be able to do the matrix multiplication in the following way, which has linear time complexity for long sequences in transformers:

[math]\displaystyle{ \begin{bmatrix} V & \Phi^T & \Phi \end{bmatrix} \quad \text{with dimensions:} \quad \begin{bmatrix} m \times n & n \times r’ & r’ \times n \end{bmatrix} = m \times n }[/math]

Steps in Kernel Approximation

• Kernel Formulation: Approximate [math]\displaystyle{ \phi(x)^T \phi(y) }[/math] as a function of random vectors.
• Random Feature Transformation: Performers use sinusoidal functions (sine and cosine) as random features for approximating similarity between sequences.
• The softmax can also be approximated using random features, with a specific [math]\displaystyle{ \varphi(x) }[/math] tailored for softmax.

[math]\displaystyle{ e^{-\frac{1}{2}\lVert x - y \rVert^2} = e^{-\frac{(x - y)^T (x - y)}{2}} = e^{-\frac{x^T x + y^T y - 2 x^T y}{2}} = e^{-\frac{x^T x}{2}} \cdot e^{-\frac{y^T y}{2}} \cdot e^{x^T y} }[/math] [math]\displaystyle{ e^{x^T y} = e^{-\lVert x - y \rVert^2} \cdot e^{\frac{x^T x}{2}} \cdot e^{\frac{y^T y}{2}} = \varphi_{\text{Gauss}}(x)^T \varphi_{\text{Gauss}}(y) \cdot e^{\frac{x^T x}{2}} \cdot e^{\frac{y^T y}{2}} = \varphi_{\text{Gauss}}(x)^T e^{\frac{x^T x}{2}} \cdot \varphi_{\text{Gauss}}(y) e^{\frac{y^T y}{2}} }[/math]

• So, the kernel approximation for the softmax is:

[math]\displaystyle{ \varphi_{\text{SM}}(x) = \frac{e^{\frac{x^T x}{2}}}{\sqrt{r}} \begin{pmatrix} \sin(\omega_1^T x), & \sin(\omega_2^T x), & \dots, & \sin(\omega_r^T x), \cos(\omega_1^T x), & \cos(\omega_2^T x), & \dots, & \cos(\omega_r^T x)\end{pmatrix} }[/math]

Variational Auto-encoders (VAEs)

• Overview: VAEs are a type of generative model that extends traditional auto-encoders by introducing stochastic elements. While traditional auto-encoders are deterministic and focus on reconstructing inputs, VAEs aim to learn a distribution over the latent space. This approach extends traditional autoencoders by introducing a probabilistic framework that enables them to capture complex data distributions.

Background: Auto-encoders

• Basic Structure: Consists of an encoder, a bottleneck layer, and a decoder.
• Objective: Maps input [math]\displaystyle{ x }[/math] into a lower-dimensional representation ([math]\displaystyle{ z = u^Tx }[/math]) by compressing it and reconstructs it. It minimizes the differences in [math]\displaystyle{ x }[/math] and the reconstructed version of it ([math]\displaystyle{ \hat{x} = uz }[/math]): [math]\displaystyle{ \min \lvert x - \hat{x} \rvert }[/math]
• PCA Connection: A simple, linear auto-encoder resembles PCA in dimensionality reduction.
• Limitation: While VAEs are powerful, they may struggle to capture highly complex data distributions compared to more recent generative models like GANs.

Moving to Variational Auto-encoders

• Generative Model Aspect: Variational Auto-encoders enforce a specific distribution on [math]\displaystyle{ z }[/math], allowing them to generate new samples.
• Gaussian Distribution Constraint: By enforcing a Gaussian distribution on [math]\displaystyle{ z }[/math], the model can generate new samples in the learned data distribution. So Variational Auto-encoder introduces a prior distribution (typically Gaussian) on [math]\displaystyle{ z }[/math] and maximizes the Evidence Lower Bound (ELBO) instead of reconstruction alone.

Approximation of the Posterior Distribution

[math]\displaystyle{ p(z|x) = \frac{p(x|z) , p(z)}{p(x)} }[/math] [math]\displaystyle{ p(x) = \int_z p(x|z) , p(z) , dz }[/math]

• [math]\displaystyle{ \mathbf{q_{\theta}(z)} }[/math] is the approximate posterior distribution of the latent variable [math]\displaystyle{ z }[/math], parameterized by [math]\displaystyle{ \theta }[/math].
• Purpose of [math]\displaystyle{ \mathbf{q_{\theta}(z)} }[/math]: In a VAE, we aim to learn a latent variable [math]\displaystyle{ z }[/math] that represents the underlying structure of the data [math]\displaystyle{ x }[/math]. Ideally, we want the true posterior [math]\displaystyle{ p(z|x) }[/math], which is often intractable to compute directly. To address this, we approximate [math]\displaystyle{ p(z|x) }[/math] with a simpler distribution [math]\displaystyle{ q_{\theta}(z|x) }[/math], where [math]\displaystyle{ \theta }[/math] represents the parameters (typically learned through a neural network).
• Key Points about [math]\displaystyle{ \mathbf{q_{\theta}(z)} }[/math]:
  • Approximate Posterior: [math]\displaystyle{ q_{\theta}(z|x) }[/math] is an approximation of the true posterior [math]\displaystyle{ p(z|x) }[/math].
  • Parameterized by [math]\displaystyle{ \mathbf{\theta} }[/math]: The parameters [math]\displaystyle{ \theta }[/math] define the structure of this distribution, often through a neural network in a VAE.
  • Optimization: During training, we optimize [math]\displaystyle{ \theta }[/math] to make [math]\displaystyle{ q_{\theta}(z|x) }[/math] as close as possible to [math]\displaystyle{ p(z|x) }[/math] by minimizing the KL divergence between [math]\displaystyle{ q_{\theta}(z|x) }[/math] and [math]\displaystyle{ p(z|x) }[/math]: [math]\displaystyle{ \min_{\theta} \text{KL} \left( q_{\theta}(z) || p(z|x) \right) }[/math]

Information Theory

In VAEs, the model learns a latent space where each data point is mapped not to a single point, but to a probability distribution. This design choice allows the VAE to: Capture the information content of the input data in a compressed, structured form. Represent the uncertainty in the data by encoding it as a distribution rather than as a single deterministic vector. The VAE learns this by balancing reconstruction accuracy with the information-theoretic regularization of the latent space, which enforces a smooth and organized representation.

• Information content:
  • [math]\displaystyle{ I }[/math], represents the information content or self-information of an event with probability [math]\displaystyle{ p(x) }[/math]. It quantifies how much “surprise” or “information” is associated with a specific outcome [math]\displaystyle{ x }[/math] occurring.
  • The formula for information content [math]\displaystyle{ I }[/math] of an event [math]\displaystyle{ x }[/math] is: [math]\displaystyle{ I = -\log p(x) }[/math]
  • [math]\displaystyle{ I }[/math] is higher for less probable events (low [math]\displaystyle{ p(x) }[/math]), indicating more “surprise” or “information” content when that event occurs.
  • In information theory, this concept helps quantify the amount of information gained from observing an event, with rare events providing more information than common ones.
  • For example, given a sentence "Tomorrow, it either rains, or not." [math]\displaystyle{ p(x) = 1 }[/math] and so [math]\displaystyle{ I = -log(1) = 0 }[/math] since there is no insight to glean in that sentence.
• Entropy:
  • [math]\displaystyle{ H }[/math] represents entropy. Entropy measures the average amount of information (or “uncertainty”) contained in a random variable. It is often used to quantify the uncertainty or unpredictability of a probability distribution.
  • The formula for entropy [math]\displaystyle{ H }[/math] of a discrete random variable [math]\displaystyle{ x }[/math] with a probability distribution [math]\displaystyle{ p(x) }[/math] is: [math]\displaystyle{ H = -\sum p(x) \log p(x) }[/math]
  • [math]\displaystyle{ H }[/math] is maximized when the distribution is most uncertain (e.g., in a uniform distribution).
  • In the context of VAEs, entropy is used to understand the distribution of latent variables and how much “information” or “uncertainty” they contain.
• KL divergence:
  • KL divergence, stands for the Kullback-Leibler divergence between two probability distributions [math]\displaystyle{ q }[/math] and [math]\displaystyle{ p }[/math]. It is a measure of how one probability distribution [math]\displaystyle{ q }[/math] diverges from a second, reference probability distribution [math]\displaystyle{ p }[/math].
  • The KL divergence from [math]\displaystyle{ q(x) }[/math] to [math]\displaystyle{ p(x) }[/math] is defined as: [math]\displaystyle{ \text{KL}(q || p) = \sum q(x) \log q(x) - \sum q(x) \log p(x) = \sum_x q(x) \log \frac{q(x)}{p(x)} }[/math]
  • KL divergence is not symmetric; [math]\displaystyle{ \text{KL}(q \| p) \neq \text{KL}(p \| q) }[/math]. This means that it matters which distribution we consider as the reference.
  • KL divergence is always non-negative, [math]\displaystyle{ \text{KL}(q \| p) \geq 0 }[/math], and equals zero if and only if [math]\displaystyle{ q = p }[/math] (almost everywhere). This is known as Gibbs’ inequality.
  • In variational inference and variational auto-encoders (VAEs), KL divergence is used to measure the difference between the approximate posterior [math]\displaystyle{ q_{\theta}(z|x) }[/math] and the true posterior [math]\displaystyle{ p(z|x) }[/math]. Minimizing [math]\displaystyle{ \text{KL}(q_{\theta}(z|x) | p(z|x)) }[/math] helps make the approximation [math]\displaystyle{ q_{\theta}(z|x) }[/math] closer to the true posterior.
  • KL divergence quantifies the “information loss” if we approximate [math]\displaystyle{ p(x) }[/math] with [math]\displaystyle{ q(x) }[/math]. In essence, it tells us how much extra information (or “surprise”) is needed to describe samples from [math]\displaystyle{ q }[/math] as if they were from [math]\displaystyle{ p }[/math].
  • For the continuous space:

[math]\displaystyle{ \text{KL}(q(z) \| p(z|x)) = -\int q(z) \log \frac{p(z|x)}{q(z)} \, dz }[/math] [math]\displaystyle{ p(z|x) = \frac{p(x|z) \, p(z)}{p(x)} }[/math] [math]\displaystyle{ p(x|z) \, p(z) = p(x,z) }[/math] [math]\displaystyle{ \text{KL}(q(z) \| p(z|x))= -\int q(z) \log \frac{p(x, z)}{q(z) \cdot p(x)} \, dz }[/math] [math]\displaystyle{ = -\int q(z) \left[ \log \frac{p(x, z)}{q(z)} + \log \frac{1}{p(x)} \right] dz }[/math] [math]\displaystyle{ = -\int q(z) \log \frac{p(x, z)}{q(z)} \, dz + \int q(z) \log p(x) \, dz = -\int q(z) \log \frac{p(x, z)}{q(z)} \, dz + \log p(x) \int q(z) \, dz }[/math] [math]\displaystyle{ \int q(z) \, dz = 1 }[/math] [math]\displaystyle{ \log p(x) = \text{KL}(q(z) \| p(z|x)) + \int q(z) \log \frac{p(x, z)}{q(z)} \, dz = \text{KL}(q(z) \| p(z|x)) + \text{ELBO} }[/math] [math]\displaystyle{ \text{ELBO} = \int q(z) \log \frac{p(x, z)}{q(z)} \, dz }[/math] [math]\displaystyle{ = \int q(z) \log \frac{p(x|z) \, p(z)}{q(z)} \, dz }[/math] [math]\displaystyle{ = \int q(z) \left[ \log p(x|z) + \log \frac{p(z)}{q(z)} \right] dz }[/math] [math]\displaystyle{ = \int q(z) \log p(x|z) \, dz + \int q(z) \log \frac{p(z)}{q(z)} \, dz }[/math] [math]\displaystyle{ = \mathbb{E}_{q(z)}[\log p(x|z)] - \text{KL}(q(z) \| p(z)) }[/math] [math]\displaystyle{ \text{ELBO} = \mathbb{E}_{q_{\theta}(z|x)}[\log p(x|z)] - \text{KL}(q_{\theta}(z|x) | p(z)) }[/math]

KL Divergence and Evidence Lower Bound (ELBO)

• KL Divergence: Measures the similarity between two distributions; minimized to bring [math]\displaystyle{ q }[/math] close to [math]\displaystyle{ p }[/math].
• Evidence Lower Bound (ELBO):
  • Variational auto-encoders maximize ELBO which is similar to minimizing KL divergence since [math]\displaystyle{ log(p(x)) }[/math] is a constant.
  • Maximizing ELBO ensures [math]\displaystyle{ q }[/math] closely approximates [math]\displaystyle{ p }[/math], meaning maximizing ELBO ensures that the learned latent distribution is close to the target distribution. This approach allows VAEs to generate new samples by sampling from the latent space.

ELBO Decomposition

• ELBO Equation: [math]\displaystyle{ ELBO = q(z) log p(x|z) - KL[q(z) || p(z)] }[/math]
• First Term: Reconstruction likelihood (maximize this).
• Second Term: Ensures latent variable [math]\displaystyle{ z }[/math] approximates the desired distribution.

Practical Implementation: Reconstruction Loss and Gaussian Constraint

• Objective in VAE Training:
  • Minimize reconstruction loss (similar to traditional auto-encoders).
  • Ensure [math]\displaystyle{ z }[/math] follows a Gaussian distribution.
• Regularization Term in ELBO: In VAEs, the Evidence Lower Bound (ELBO) includes a KL divergence term to ensure that the learned latent distribution remains close to a prior distribution (e.g., a Gaussian [math]\displaystyle{ p(z) = N(0, I) }[/math]).

Re-parameterization Trick

• Challenge: The stochastic nature of [math]\displaystyle{ z }[/math] complicates backpropagation.
• Solution: To make the stochastic layer differentiable, VAEs use the re-parameterization trick, where [math]\displaystyle{ z }[/math] is expressed as a deterministic function with a noise component. So we use re-parameterization to enable gradient-based optimization and we minimize:

[math]\displaystyle{ \min \left( \lvert x - \hat{x} \rvert^2 + \text{KL}(q(z) \| N(0, 1)) \right) }[/math]

Reverse Processes

• We need to know the reverse diffusion process [math]\displaystyle{ p_{\theta}(x_{t-1}|x_t)=N(x_{t-1};\mu_{\theta}(x_t,t),\Sigma_{\theta}(x_t,t)) }[/math]
• Mean of q(x_{t-1}|x_t,x_0):

[math]\displaystyle{ \begin{align} q(x_{t-1}|x_t,x_0) &= q(x_{t}|x_{t-1},x_0) \frac{q(x_{t-1}|x_0)}{q(x_t|x_0)} \\ &\propto \exp\left( -\frac{1}{2} \left( \frac{(x_t - \sqrt{\alpha_t}x_{t-1})^2}{\beta_t} + \frac{(x_{t-1} - \sqrt{\bar{\alpha}_{t-1}}x_{0})^2}{1-\bar{\alpha}_{t-1}} - \frac{(x_t - \sqrt{\bar{\alpha}_{t}}x_{0})^2}{1-\bar{\alpha}_{t}} \right) \right)\\ &= \exp\left( -\frac{1}{2} \left( \left( \frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha_{t-1}}} \right) x_{t-1}^2 - \left( \frac{2\sqrt{\alpha_t}}{\beta_t} x_t + \frac{2\sqrt{\bar{\alpha_{t-1}}}}{1-\bar{\alpha_{t-1}}} x_0 \right) x_{t-1} + C(x_t,x_0) \right) \right) \end{align} }[/math]

, where [math]\displaystyle{ C(x_t,x_0) }[/math] is not a function of [math]\displaystyle{ x_{t-1} }[/math]

Define [math]\displaystyle{ \alpha_t=1-\beta_t, \bar{\alpha_t}=\prod_{i=1}^T{\alpha_i} }[/math],

[math]\displaystyle{ \tilde{\mu_t}(x_t,x_0)=\frac{\sqrt{\alpha_t}(1-\bar{\alpha_{t-1}})}{1-\bar{\alpha_t}}x_t + \frac{\sqrt{\bar{\alpha_{t-1}}}\beta_t}{1-\bar{\alpha_t}}x_0 }[/math]

Since [math]\displaystyle{ x_0=\frac{1}{\sqrt{\bar{\alpha_t}}}(x_t-\sqrt{1-\bar{\alpha_t}}\epsilon_t) }[/math], we have

[math]\displaystyle{ \tilde{\mu_t}(x_t,x_0)=\frac{1}{\sqrt{\bar{\alpha_t}}}\left(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha_t}}}\epsilon_t\right) }[/math]

• KL for two Gaussian

Between forward process and backward process:

[math]\displaystyle{ D_{KL}(q(x_{t-1} | x_t, x_0) | p_\theta(x_{t-1} | x_t)) }[/math]

For the distributions:

[math]\displaystyle{ q(x) = \mathcal{N}(x; \mu_q, \Sigma_q) }[/math] and [math]\displaystyle{ p(x) = \mathcal{N}(x; \mu_p, \Sigma_p) }[/math],

The KL divergence formula is:

[math]\displaystyle{ D_{KL}(q | p) = \frac{1}{2} \left( \text{tr}(\Sigma_p^{-1} \Sigma_q) + (\mu_p - \mu_q)^T \Sigma_p^{-1} (\mu_p - \mu_q) - k + \ln \left( \frac{\det \Sigma_p}{\det \Sigma_q} \right) \right) }[/math]

For [math]\displaystyle{ q }[/math]:

[math]\displaystyle{ \tilde{\mu}_t(x_t, x_0) = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon \right) }[/math]

For [math]\displaystyle{ p }[/math]:

[math]\displaystyle{ \mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}t}} \epsilon\theta(x_t, t) \right) }[/math]

• Loss function

The loss function is defined as:

[math]\displaystyle{ L_t = \mathbb{E}{x_0, \epsilon} \left[ \frac{1}{2 | \Sigma\theta(x_t, t) |_2^2} | \tilde{\mu}t(x_t, x_0) - \mu\theta(x_t, t) |^2 \right] }[/math]

Substituting [math]\displaystyle{ \tilde{\mu}t }[/math] and [math]\displaystyle{ \mu\theta }[/math]:

[math]\displaystyle{ L_t = \mathbb{E}{x_0, \epsilon} \left[ \frac{1}{2 | \Sigma\theta |_2^2} \left| \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_t \right) - \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}t}} \epsilon\theta(x_t, t) \right) \right|^2 \right] }[/math]

Simplifying:

[math]\displaystyle{ L_t = \mathbb{E}_{x_0, \epsilon} \left[ \frac{(1 - \alpha_t)^2}{2 \alpha_t (1 - \bar{\alpha}t) | \Sigma\theta |2^2} | \epsilon_t - \epsilon\theta(x_t, t) |^2 \right] }[/math]

Expressing [math]\displaystyle{ x_t }[/math] in terms of [math]\displaystyle{ x_0 }[/math] and [math]\displaystyle{ \epsilon }[/math]:

[math]\displaystyle{ L_t = \mathbb{E}_{x_0, \epsilon} \left[ \frac{(1 - \alpha_t)^2}{2 \alpha_t (1 - \bar{\alpha}t) | \Sigma\theta |2^2} | \epsilon_t - \epsilon\theta(\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, t) |^2 \right] }[/math]

Graph Neural Network (GNN)

Graph Neural Networks are a class of deep learning methods designed to perform inference on data described by graphs.

Application

• Graphs are Structured Data: Many real-world datasets can be represented as graphs. Examples: social networks, protein-interaction networks, the World Wide Web, and molecules, where entities and their relationships are mapped as nodes and edges. In social networks, each user can be represented as a node and the relationships or interactions between them — such as friendships and follows — are represented as edges connecting the nodes. GNN can be used to recommend friends and content by learning from the network structure. Also, GNN can help to track the spread of information or behaviors across the network.

• Images as Graphs: Images can be considered as graphs where each pixel acts as a node. In this representation, each pixel node connects to its adjacent pixels through edges and form a grid-like graph structure that captures the spatial relationships in the image.

• Text as Graphs: Text data can also be represented as graphs. Here, each token or word is a node, and each node is connected by edges to the preceding and following tokens, which can capture the sequential dependencies in the text.

• CNN as GNN: Convolutional Neural Networks (CNNs) can be viewed as a specialized form of Graph Neural Networks (GNNs) applied to grid-like structures. Each pixel in an image represents a node connected to its neighbors, with convolutions aggregating features across the whole grid. The main goal is to check if convolution can be defined on random graphs.

Tasks

There are 3 different levels of tasks.

• Graph-Level Tasks: These involve predicting a property of the entire graph. For example, in molecular graphs, we may predict whether a particular molecule will bind to a receptor based on the graph structure. Examples: Images, Differentiate between molecules.
• Node-Level Tasks: These focus on predicting the identity or role of each individual node within the graph. This could involve classifying nodes based on their attributes or their position within the network. Example: Node belonging to a network.
• Edge-Level Tasks: These involve analyzing or predicting relationships between pairs of nodes, such as determining whether two nodes in a social network graph are friends or not. Example: Recommender Systems.

Graph

Definition

A graph, denoted as [math]\displaystyle{ G }[/math], can be defined by a set of vertices (or nodes) [math]\displaystyle{ V }[/math] and edges (connections between the vertices) [math]\displaystyle{ V }[/math], along with an adjacency matrix [math]\displaystyle{ A }[/math]. This matrix represents the relationships between vertices in a binary format.

In graph notation, we write this as [math]\displaystyle{ G = (V, E, A) }[/math], where:

• [math]\displaystyle{ V }[/math]: Vertices or nodes in the graph.
• [math]\displaystyle{ E }[/math]: Edges, which indicate connections between pairs of vertices.
• [math]\displaystyle{ A }[/math]: Adjacency matrix, a binary matrix that indicates the presence (1) or absence (0) of an edge between vertex pairs.

The adjacency matrix is a binary matrix indicating whether pairs of vertices are adjacent and is structured so that:

The entry [math]\displaystyle{ A_{ij} = 1 }[/math] if there is an edge between vertex [math]\displaystyle{ i }[/math] and vertex [math]\displaystyle{ j }[/math]. The entry [math]\displaystyle{ A_{ij} = 0 }[/math] if there is no edge between vertex [math]\displaystyle{ i }[/math] and vertex [math]\displaystyle{ j }[/math].

In this way, the adjacency matrix provides a clear view of the connections within the graph.

Laplacian of a Graph

Laplacian Matrix Definition

[math]\displaystyle{ L = D - A }[/math]

[math]\displaystyle{ D }[/math]: Degree matrix, which is a diagonal matrix where each diagonal entry represents the degree of each vertex.

[math]\displaystyle{ A }[/math]: Adjacency matrix, as previously defined.

Degree Matrix Notation

The degree matrix [math]\displaystyle{ D }[/math] is a square matrix in which each diagonal element [math]\displaystyle{ d_i }[/math] represents the degree of the corresponding vertex [math]\displaystyle{ i }[/math]. [math]\displaystyle{ D = \begin{bmatrix} d_1 & 0 & \dots & 0 \\ 0 & d_2 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & d_n \end{bmatrix}_{n \times n} }[/math]

Degree of a Vertex is defined as [math]\displaystyle{ d_i = \sum_j A_{ij} }[/math]. The degree [math]\displaystyle{ d_i }[/math] is the sum of the elements in the [math]\displaystyle{ i }[/math]-th row of [math]\displaystyle{ A }[/math], representing the number of edges connected to vertex [math]\displaystyle{ i }[/math].

Example

For an adjacency matrix [math]\displaystyle{ A }[/math] as follows:

[math]\displaystyle{ A = \begin{bmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} }[/math]

The sum of each row (representing each vertex's degree) results in:

[math]\displaystyle{ \text{Sum} = \begin{bmatrix} \sum A_{1j} \\ \sum A_{2j} \\ \sum A_{3j} \\ \sum A_{4j} \end{bmatrix} = \begin{bmatrix} 2 \\ 2 \\ 3 \\ 1 \end{bmatrix} }[/math]

This yields the degree matrix [math]\displaystyle{ D }[/math] as:

[math]\displaystyle{ D = \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} }[/math]

The Laplacian matrix [math]\displaystyle{ L }[/math] is then calculated as:

[math]\displaystyle{ L = D - A }[/math]

Graph Cut Optimization Problem

The graph cut optimization problem aims to partition a graph into segments with minimal interconnections between them.

• Objective: The goal is to find a cut that divides the graph into distinct segments while minimizing the connections between them.
• Minimization Target: The target function to minimize is [math]\displaystyle{ \sum A_{ij} (y_i - y_j)^2 }[/math], which captures the cost associated with the "cut" between segments.
• Equation: The minimization can be expressed as [math]\displaystyle{ y^T L y }[/math], where [math]\displaystyle{ L }[/math] is the Laplacian matrix, and [math]\displaystyle{ y }[/math] is a vector representing the segment assignment of each node.
• Constraint Applied: The constraint [math]\displaystyle{ y^T y = 1 }[/math] is applied to ensure non-trivial solutions.
• Vector [math]\displaystyle{ y }[/math]: This vector represents the assignment of nodes to segments, with dimensions [math]\displaystyle{ n \times 1 }[/math], where [math]\displaystyle{ n }[/math] is the number of nodes.
• Solution Method: Optimal partitioning is achieved by performing eigen decomposition on the Laplacian matrix [math]\displaystyle{ L }[/math].

Eigen Decomposition of Laplacian

The Laplacian matrix [math]\displaystyle{ L }[/math] can be decomposed as [math]\displaystyle{ L = U \Lambda U^T }[/math], where:

[math]\displaystyle{ U }[/math] represents the orthonormal eigenvectors. These eigenvectors are both orthogonal to each other and normalized. [math]\displaystyle{ \Lambda }[/math] is a diagonal matrix containing the eigenvalues. Each diagonal entry in [math]\displaystyle{ \Lambda }[/math] corresponds to an eigenvalue that pairs with an eigenvector in [math]\displaystyle{ U }[/math].

Starting with the standard Laplacian, defined as [math]\displaystyle{ L = D - A }[/math]:

[math]\displaystyle{ D }[/math] is the degree matrix. [math]\displaystyle{ A }[/math] is the adjacency matrix. The normalized Laplacian is given by: [math]\displaystyle{ \tilde{L} = D^{-\frac{1}{2}} (D - A) D^{-\frac{1}{2}} }[/math]

This expression can be simplified to: [math]\displaystyle{ \tilde{L} = I - D^{-\frac{1}{2}} A D^{-\frac{1}{2}} }[/math], where [math]\displaystyle{ I }[/math] is the identity matrix.

Laplacian Eigenvectors and Fourier Analysis Analogy

• Mathematical Definition: Decomposition of a signal into sinusoidal components.
• Frequency Domain: A signal is transformed to represent it as a sum of its frequency components.
• Basis Functions: Sine and cosine functions serve as the basis for this transformation.
• Orthogonality: These basis functions are orthogonal, ensuring unique frequency representation.
• Graph Signals: Functions defined over the nodes of a graph.
• Spectral Domain: Eigenvectors of [math]\displaystyle{ L }[/math] transform graph signals into the spectral domain.
• Eigenvector Basis: Analogous to sines and cosines, eigenvectors form a basis for graph signals.
• Orthogonality: Eigenvectors are orthogonal, providing a unique spectral representation for graph signals.
• Low Eigenvalues: Correspond to "low-frequency" eigenvectors. These eigenvectors change slowly over the graph. Represent large-scale, smooth structures in the graph.
• High Eigenvalues: Correspond to "high-frequency" eigenvectors. These eigenvectors change rapidly between connected nodes. Capture fine details or irregularities in the graph.
• Ordering: Eigenvalues (and eigenvectors) are ordered from lowest to highest.

Fourier Transform

The eigen-decomposition of the graph Laplacian [math]\displaystyle{ L }[/math] can be written as: [math]\displaystyle{ L = U^T \Lambda U }[/math], where:

• [math]\displaystyle{ U = [u_1, ..., u_n] }[/math] is the matrix of orthonormal eigenvectors.
• [math]\displaystyle{ \Lambda }[/math] is a diagonal matrix where each entry [math]\displaystyle{ \Lambda_{ii} = \lambda_i }[/math] represents an eigenvalue (also known as the spectrum of the Laplacian).
• The equation [math]\displaystyle{ U^T U = I }[/math] indicates that the eigenvectors are orthonormal.

The eigenvectors from [math]\displaystyle{ u_1 }[/math] to [math]\displaystyle{ u_n }[/math] are also called Fourier functions, as they serve as a basis for transforming signals on the graph.

The Fourier transform projects a signal [math]\displaystyle{ x }[/math] onto the Fourier functions, resulting in coefficients that form the Fourier series.

In the context of graphs, the graph Fourier transform projects an input graph signal onto an orthonormal basis formed by the eigenvectors of the normalized graph Laplacian.

Suppose [math]\displaystyle{ x \in \mathbb{R}^n }[/math] is a feature vector containing the values of all nodes in a graph, where [math]\displaystyle{ x_i }[/math] represents the value at the [math]\displaystyle{ i }[/math]-th node.

• The graph Fourier transform of a signal [math]\displaystyle{ x }[/math] is given by: [math]\displaystyle{ f(x) = U^T x = \hat{x} }[/math]
• The inverse graph Fourier transform is defined as: [math]\displaystyle{ f^{-1}(\hat{x}) = U \hat{x} = U U^T x = x }[/math]

ConvGNNs

The graph convolution of an input signal [math]\displaystyle{ x }[/math] with a filter [math]\displaystyle{ g \in \mathbb{R}^n }[/math] is defined as follows:

Convolution Theorem: [math]\displaystyle{ f(x * g) = (f(x) \cdot f(g)) }[/math]

This can be expanded as:

• [math]\displaystyle{ x * g = f^{-1}(f(x) \cdot f(g)) }[/math]
• [math]\displaystyle{ = U (U^T x \cdot U^T g) }[/math]
• [math]\displaystyle{ = U g_\theta U^T x }[/math]

Where [math]\displaystyle{ g_\theta = \text{diag}(U^T g) }[/math].

Neural Network Layers

• Feedforward Neural Networks (FFNN):

Computation proceeds in layers, with each layer represented as [math]\displaystyle{ h' = \sigma(Wh) }[/math]. The output of each layer [math]\displaystyle{ h' }[/math] serves as the input for the next layer. The initial input [math]\displaystyle{ h_0 }[/math] is the feature vector [math]\displaystyle{ x }[/math].

• Convolutional Neural Networks (CNN):

Layer computation involves convolution, with each layer defined as [math]\displaystyle{ h' = \sigma(w * h) }[/math]. [math]\displaystyle{ w }[/math] represents the learned filters or kernels that slide over [math]\displaystyle{ h }[/math].

Vanilla Spectral GNN

The graph convolutional layer of the Spectral CNN is defined as:

[math]\displaystyle{ x * g = f^{-1}(f(x) \cdot f(g)) }[/math] [math]\displaystyle{ = U (U^T x \cdot U^T g) }[/math] [math]\displaystyle{ = U g_\theta U^T x }[/math]

With:

• [math]\displaystyle{ H' = \sigma(U \Theta U^T H) }[/math]
• [math]\displaystyle{ X = H^{(0)} }[/math]
• [math]\displaystyle{ g_\theta = \Theta }[/math]

Here, [math]\displaystyle{ \Theta }[/math] is a diagonal matrix with learnable parameters, where [math]\displaystyle{ U^T g = \begin{bmatrix} u_1^T g \ \vdots \ u_n^T g \end{bmatrix} }[/math] and [math]\displaystyle{ \Theta = \begin{bmatrix} u_1^T g & \dots & u_n^T g \end{bmatrix} }[/math].

Limitation: Eigen-decomposition requires [math]\displaystyle{ O(n^2) }[/math] computational complexity.

ChebNet

Approximates the filter [math]\displaystyle{ g_\theta }[/math] by Chebyshev [*] polynomials of the diagonal matrix of eigenvalues [math]\displaystyle{ \Lambda }[/math].

Chebyshev Polynomials of the first kind

• [math]\displaystyle{ T_0(x) = 1 }[/math]
• [math]\displaystyle{ T_1(x) = x }[/math]
• For [math]\displaystyle{ i \geq 2 }[/math], the polynomials are defined as: [math]\displaystyle{ T_i(x) = 2x T_{i-1}(x) - T_{i-2}(x) }[/math]

ChebNet Graph Convolution

• [math]\displaystyle{ g_{\theta}=\sum_{i}{\theta_i{T_i}(\tilde{\Alpha}}) }[/math].
• [math]\displaystyle{ g_{\theta} }[/math] is a Graph convolutional filter with parameter [math]\displaystyle{ \theta }[/math].
• [math]\displaystyle{ \tilde{\Alpha} }[/math] is are scaled eigenvalues of the Laplacian matrix: [math]\displaystyle{ \tilde{\Alpha}=\frac{2\Alpha}{\lambda_{max}}-I_n }[/math], which makes the normalized eigenvalues fall into [-1,1].
• [math]\displaystyle{ x*{g}=Ug_{\theta}U^Tx }[/math]
• [math]\displaystyle{ x*{g}=\sum_{i}\theta_iUT_i(\tilde{\Alpha})U^Tx }[/math]
• [math]\displaystyle{ x*{g_{\theta}}=U\left(\sum_{i}\theta_iT_i(\tilde{\Alpha})\right)U^Tx }[/math]
• This is equal to: [math]\displaystyle{ x*{g_{\theta}}=\sum_{i=1}^k{\theta_iT_i(\tilde{L})x} }[/math], where [math]\displaystyle{ \tilde{L}=\frac{2L}{\lambda_{max}}-I_n }[/math]