stat946w18/Tensorized LSTMs
Presented by
Chen, Weishi(Edward)
Introduction
Long Short-Term Memory (LSTM) is a popular approach to boosting the ability of Recurrent Neural Networks to store longer term temporal information. The capacity of an LSTM network can be increased by widening and adding layers (illustrations will be provided later).
However, usually the LSTM model introduces additional parameters, while LSTM with additional layers and wider layers increases the time required for model training and evaluation. As an alternative, the paper <Wider and Deeper, Cheaper and Faster: Tensorized LSTMs for Sequence Learning> has proposed a model based on LSTM call the Tensorized LSTM in which the hidden states are represented by tensors and updated via a cross-layer convolution.
- By increasing the tensor size, the network can be widened efficiently without additional parameters since the parameters are shared across different locations in the tensor
- By delaying the output, the network can be deepened implicitly with little additional runtime since deep computations for each time step are merged into temporal computations of the sequence.
Also, the paper has presented presented experiments conducted on five challenging sequence learning tasks show the potential of the proposed model.
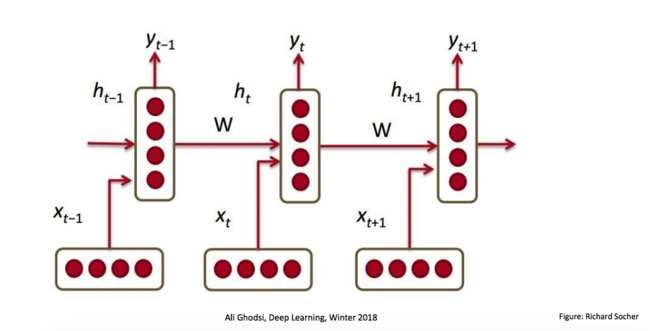
A Quick Introduction to RNN and LSTM
We consider the time-series prediction task of producing a desired output [math]\displaystyle{ y_t }[/math] at each time-step t∈ {1, ..., T} given an observed input sequence [math]\displaystyle{ x1: t = {x_1,x_2, ···, x_t} }[/math], where [math]\displaystyle{ x_t∈R^R }[/math] and [math]\displaystyle{ y_t∈R^S }[/math] are vectors. RNN learns how to use a hidden state vector [math]\displaystyle{ h_t ∈ R^M }[/math] to encapsulate the relevant features of the entire input history x1:t (indicates all inputs from to initial time-step to final step before predication - illustration given below) up to time-step t.
\begin{align} h_{t-1}^{cat} = [x_t, h_{t-1}] \hspace{2cm} (1) \end{align}
Where [math]\displaystyle{ h_{t-1}^{cat} ∈R^{R+M} }[/math] is the concatenation of the current input [math]\displaystyle{ x_t }[/math] and the previous hidden state [math]\displaystyle{ h_{t−1} }[/math], which expands the dimensionality of intermediate information.
The update of the hidden state ht is defined as:
\begin{align} a_{t} =h_{t-1}^{cat} W^h + b^h \hspace{2cm} (2) \end{align}
and
\begin{align} h_t = \Phi(a_t) \hspace{2cm} (3) \end{align}
[math]\displaystyle{ W^h∈R^(R+M)xM }[/math] guarantees each hidden status provided by the previous step is of dimension M. [math]\displaystyle{ a_t ∈R^M }[/math] the hidden activation, and φ(·) the element-wise "tanh" function. Finally, the output [math]\displaystyle{ y_t }[/math] at time-step t is generated by:
\begin{align} y_t = \varphi(h_{t}^{cat} W^y + b^y) \hspace{2cm} (4) \end{align}
where [math]\displaystyle{ W^y∈R^{M×S} }[/math] and [math]\displaystyle{ b^y∈R^S }[/math], and [math]\displaystyle{ \varphi(·) }[/math] can be any differentiable function, notes that the "Phi" is the element-wise function which produces some non-linearity and further generates another hidden status, while the "Curly Phi" is applied to generates the output
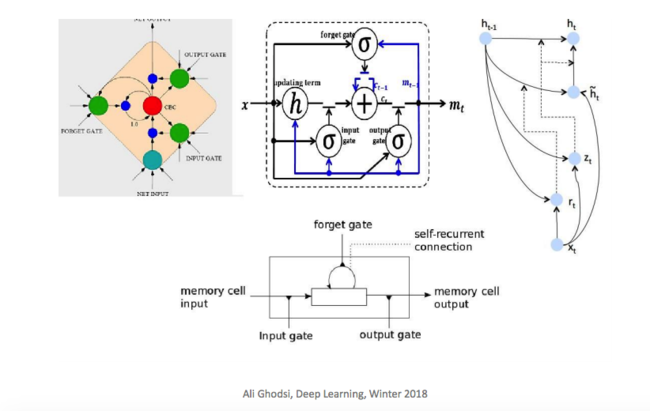
However, one shortfall of RNN is the vanishing/exploding gradients. This shortfall is more significant especially when constructing long-range dependencies models. One alternative is to apply LSTM (Long Short-Term Memories), LSTMs alleviate these problems by employing memory cells to preserve information for longer, and adopting gating mechanisms to modulate the information flow. Since LSTM is successfully in sequence models, it is natural to consider how to increase the complexity of the model to accommodate more complex analytical needs.
Structural Measurement of Sequential Model
We can consider the capacity of a network consists of two components: the width (the amount of information handled in parallel) and the depth (the number of computation steps).
A way to widen the LSTM is to increase the number of units in a hidden layer; however, the parameter number scales quadratically with the number of units. To deepen the LSTM, the popular Stacked LSTM (sLSTM) stacks multiple LSTM layers. The drawback of sLSTM, however, is that runtime is proportional to the number of layers and information from the input is potentially lost (due to gradient vanishing/explosion) as it propagates vertically through the layers. This paper introduced a way to both widen and deepen the LSTM whilst keeping the parameter number and runtime largely unchanged. In summary, we make the following contributions:
(a) Tensorize RNN hidden state vectors into higher-dimensional tensors, to enable more flexible parameter sharing and can be widened more efficiently without additional parameters.
(b) Based on (a), merge RNN deep computations into its temporal computations so that the network can be deepened with little additional runtime, resulting in a Tensorized RNN (tRNN).
(c) We extend the tRNN to an LSTM, namely the Tensorized LSTM (tLSTM), which integrates a novel memory cell convolution to help to prevent the vanishing/exploding gradients.
Method
Go through the methodology.