what game are we playing

Authors

Yuxin Wang, Evan Peters, Yifan Mou, Sangeeth Kalaichanthiran

Learning Extensive form games

The normal form representation for games where players have _many_ choices quickly becomes intractable. For example, consider a chess game: One the first turn, player 1 has 20 possible moves and then player 2 has 20 possible responses. If in the following number of turns each player is estimated to have ~30 possible moves and if a typical game is 40 moves per player, the total number of strategies is roughly [math]\displaystyle{ 10^{120} }[/math] per player (this is known as the Shannon number for game-tree complexity of chess) and so the payoff matrix for a typical game of chess must therefore have [math]\displaystyle{ O(10^{240}) }[/math] entries.

Instead, it is much more useful to represent the game graphically (in "Extensive form"). We'll also need to consider types of games where there is incomplete information - players do not necessarily have access to the full state of the game. An example of this is one-card poker: (1) Each player draws a single card from a 13-card deck (ignore suits) (2) Player 1 decides whether to bet/hold (3) Player 2 decides whether to call/raise (4) Player 1 must either call/fold if Player 2 raised. From this description, player 1 has [math]\displaystyle{ 2^{13} }[/math] possible first moves (all combinations of (card, raise/hold)) and has [math]\displaystyle{ 2^{13} }[/math] possible second moves (whenever player 1 gets a second move) for a total of [math]\displaystyle{ 2^{26} }[/math] possible strategies. In addition, Player 1 never knows what cards player 2 has and vice versa. So instead of representing the game with a huge payoff matrix we can instead represent it as a simple decision tree:

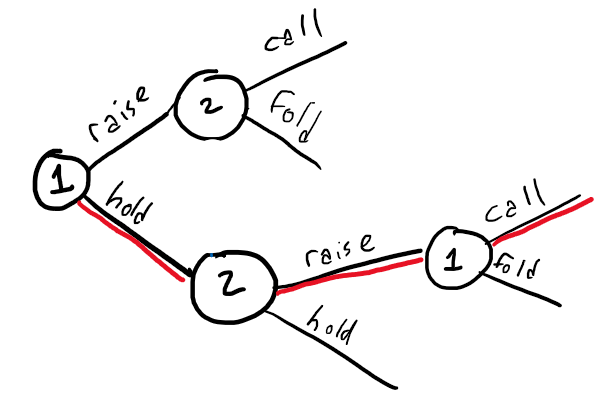
where player 1 is represented by "1", a node that has two branches corresponding to the allowed moves of player 1. However there must also be a notion of information available to either player; player 1 does not know what card player 2 has, and so player 2's decisions