The Curious Case of Degeneration
Presented by
Donya Hamzeian
Introduction
Text generation is the act of automatically generating natural language texts like summarization, neural machine translation, fake news generation and etc. Degeneration happens when the output text is incoherent or produces repetitive results. For example in the figure below, the GPT2 model tries to generate the continuation text given the context. On the left side, the beam-search was used as the decoding strategy which has obviously stuck in a repetitive loop. On the right side, however, you can see how the pure sampling decoding strategy has generated incoherent results.

The authors argue that decoding strategies that are based on maximization like beam search lead to degeneration even with powerful models like GPT-2. Even though there are some utility functions that encourage diversity, they are not enough and the text generated by maximization, beam-search, or top-k sampling is too probable which indicates the lack of diversity (variance) compared to human-generated texts
Some may raise this question that the problem with beam-search may be due to search error i.e. they are more probable phrases that beam search is unable to find, but the point is that natural language has lower per-token probability on average and people usually optimize against saying the obvious.
The authors blame the long, unreliable tail in the probability distribution of tokens that the model samples from i.e. vocabularies with low probability frequently appear in the output text. So, top-k sampling with high values of k may produce texts closer to human texts, yet they have high variance in likelihood leading to incoherency issues. Therefore, instead of fixed k, it is good to dynamically increase or decrease the number of candidate tokens. Nucleus Sampling which is the contribution of this paper does this expansion and contraction of the candidate pool.
Language Model Decoding
There are two types of generation tasks.
1. Directed generation tasks: In these tasks, there are pairs of (input, output) that the model tries to generate the output text which is tightly scoped by the input text. Because of this constraint, these tasks less suffer from the degeneration. Summarization, neural machine translation, and input-to-text generation are some examples of these tasks.
2. Open-ended generation tasks like conditional story generation or the tasks like in the above figure have high degrees of freedom. As a result, degeneration is more frequent in these tasks, and in fact, they are the focus of this paper.
The goal of the open-ended tasks is to generate the next n continuation tokens given a context sequence with m tokens. That is to maximize the following probability.
Nucleus Sampling
This decoding strategy is indeed truncating the long tail of the probability distribution. In order to do that, first, we need to find the smallest vocabulary set [math]\displaystyle{ V^{(p)} }[/math] which satisfies [math]\displaystyle{ \Sigma_{x \in V^{(p)}} P(x|x_{1:i-1}) \ge p }[/math]. Then set p'= [math]\displaystyle{ \Sigma_{x \in V^{(p)}} P(x|x_{1:i-1}) \ge p }[/math] and rescale the probability distribution with p' and select the tokens from P'. [math]\displaystyle{ P'(x|x_{1:i-1} = \begin{cases} \frac{P(x|x_{1:i-1})}{p'}, & \mbox{if } x \in V^{(p)} \\ 0 & \mbox{if } otherwise \end{cases} }[/math]
Top-k Sampling
Top-k sampling also relies on truncating the distribution. In this decoding strategy, we need to first find a set of tokens with size k [math]\displaystyle{ V^{(k)} }[/math] which maximizes [math]\displaystyle{ \Sigma_{x \in V^{(k)}} P(x|x_{1:i-1}) }[/math] and set [math]\displaystyle{ p' = \Sigma_{x \in V^{(k)}} P(x|x_{1:i-1}) }[/math]. Finally, rescale the probability distribution similar to the Nucleus sampling.
Sampling with Temperature
The probability of tokens will be calculated according to the equation below where 0<t<1 and [math]\displaystyle{ u_{1:|V|} }[/math] are logits. Recent studies have shown that lowering t improves the quality of the generated texts while it decreases diversity.
[math]\displaystyle{ P(x= V_l|x_{1:i-1}) = \frac{\exp(\frac{u_l}{t})}{\Sigma_{l'}\exp(\frac{u'_l}{t})} }[/math]
Likelihood Evaluation
To see the results of the nucleus decoding strategy, they used GPT2-large that was trained on WebText to generate 5000 text documents conditioned on initial paragraphs with 1-40 tokens.
Perplexity
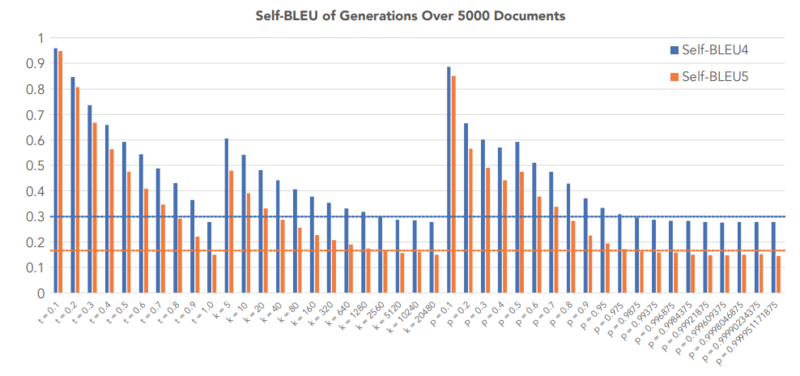
This score was used to compare the coherence of different decoding strategies. By looking at the graphs below, it is possible for Sampling, Top-k sampling, and Nucleus strategies to be tuned such that they achieve a perplexity close to the perplexity of human-generated texts; however, with the best parameters according to the perplexity the first two strategies generate low diversity texts.
Distributional Statistical Evaluation
Zipf Distribution Analysis
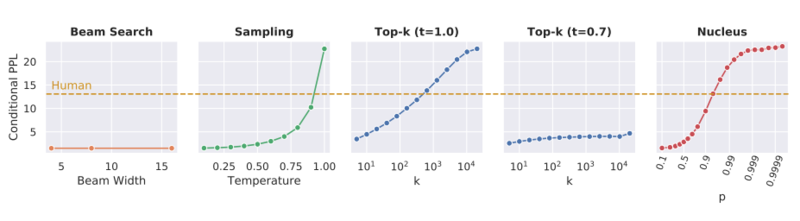
Zipf's law says that the frequency of any word is inversely proportional to its rank in the frequency table, so it suggests that there is an exponential relationship between the rank of each word with its frequency in the text. By looking at the graph below, it seems that the Zipf's distribution of the texts generated with Nucleus sampling is very close to the Zipf's distribution of the human-generated(gold) texts, while beam-search is very different from them.
Self BLEU
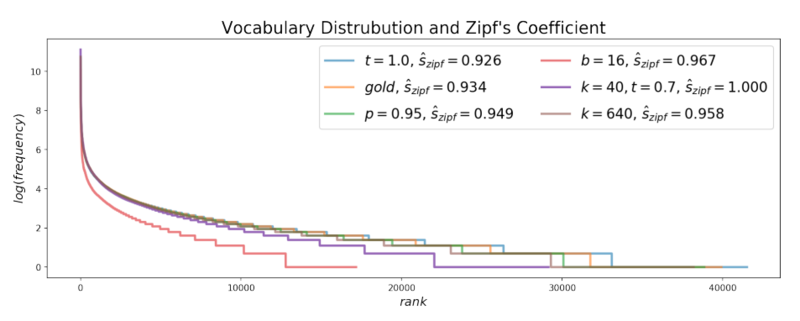
The Self-BLEU score is used to compare the diversity of each decoding strategy and was computed for each generated text using all other generations in the evaluation set as references. In the figure below, the self-BLEU score of three decoding strategies- Top-K sampling, Sampling with Temperature, and Nucleus sampling- were compared against the Self-BLEU of human-generated texts. By looking at the figure below, we see that high values of parameters that generate the self-BLEU close to that of the human texts result in incoherent, low perplexity, in Top-K sampling and Temperature Sampling, while this is not the case for Nucleus sampling.