Dynamic Routing Between Capsules STAT946
Presented by
Yang, Tong(Richard)
Introduction
Hinton's Critiques on CNN
Four arguments against pooling
- It is a bad fit to the psychology of shape perception: It does not explain why we assign intrinsic coordinate frames to objects and why they have such huge effects.
- It solves the wrong problem: We want equivariance, not invariance. Disentangling rather than discarding.
- It fails to use the underlying linear structure: It does not make use of the natural linear manifold that perfectly handles the largest source of variance in images.
- Pooling is a poor way to do dynamic routing: We need to route each part of the input to the neurons that know how to deal with it. Finding the best routing is equivalent to parsing the image.
Equivariance
- Without the sub-sampling, convolutional neural nets give "place-coded" equivariance for discrete translations.
Two types of equivariance
Place-coded equivariance
If a low-level part moves to a very different position it will be represented by a different capsule.
Rate-coded equivariance
If a part only moves a small distance it will be represented by the same capsule but the pose outputs of the capsule will change.
Higher-level capsules have bigger domains so low-level place-coded equivariance gets converted into high-level rate-coded equivariance.
== Extrapolating shape recognition to very different viewpoints
- Current neural net wisdom:
- Learn different models for different viewpoints.
- This requires a lot of training data.
- A much better approach:
- The manifold of images of the same rigid shape is highly non-linear in the space of pixel intensities.
- Transform to a space in which the manifold is globally linear
Dynamic Routing
In the second section of this paper, authors give a mathematical representations for two key features in routing algorithm in capsule network, which are squashing and agreement. The general setting for this algorithm is between two arbitrary capsules i and j. Capsule j is assumed to be an arbitrary capsule from the first layer of capsules, and capsule i is an arbitrary capsule from the layer below. The purpose of routing algorithm is generate a vector output for routing decision between capsule j and capsule i. Furthermore, this vector output will be used in the decision for choice of dynamic routing.
Routing Algorithm

Log Prior Probability
[math]\displaystyle{ b_{ij} }[/math] represents the log prior probabilities that capsule i should be coupled to capsule j, and updated in each routing iteration. In the algorithm, the initial values of [math]\displaystyle{ b_{ij} }[/math] for all possible pairs of capsules are set to 0.
Coupling Coefficient
\begin{align} c_{ij} = \frac{exp(b_ij)}{\sum_{k}exp(b_ik)} \end{align}
Capsule
Each capsule can be seen as the weighted \begin{align} s_j = \sum_{i}c_{ij}\hat{u}_{j|i} \end{align}
where
\begin{align} \hat{u}_{j|i} = W_{ij}u_i \end{align}
Squashing
\begin{align} v_j = \frac{||s_j||^2}{1+||s_j||^2}\frac{s_j}{||s_j||} \end{align}
CapsNet Architecture
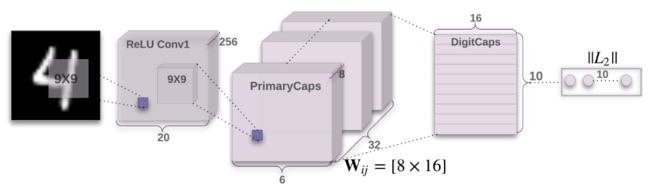
How many routing iteration to use?
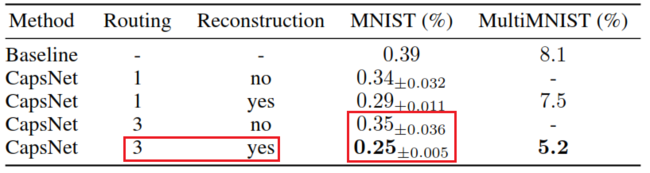
In appendix A of this paper, the authors have shown the empirical results from 500 epochs of training at different choice of routing iterations. According to their observation, more routing iterations increases the capacity of CapsNet but tends to bring additional risk of overfitting. Moreover, CapsNet with routing iterations less than three are not effective in general. As result, they suggest 3 iterations of routing for all experiments.
Decoder
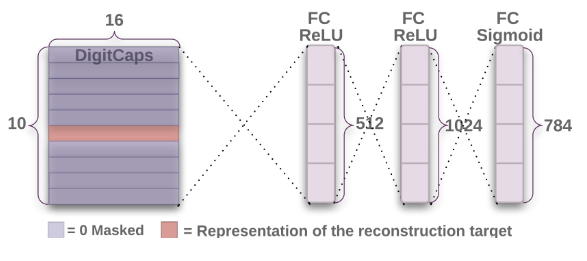
Regularization Method: Reconstruction
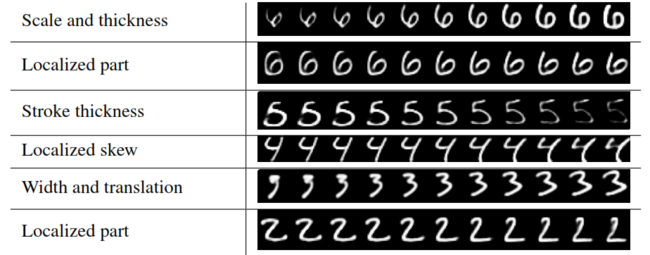
MINST
Interpretation of Each Capsule