One-Shot Imitation Learning

Introduction

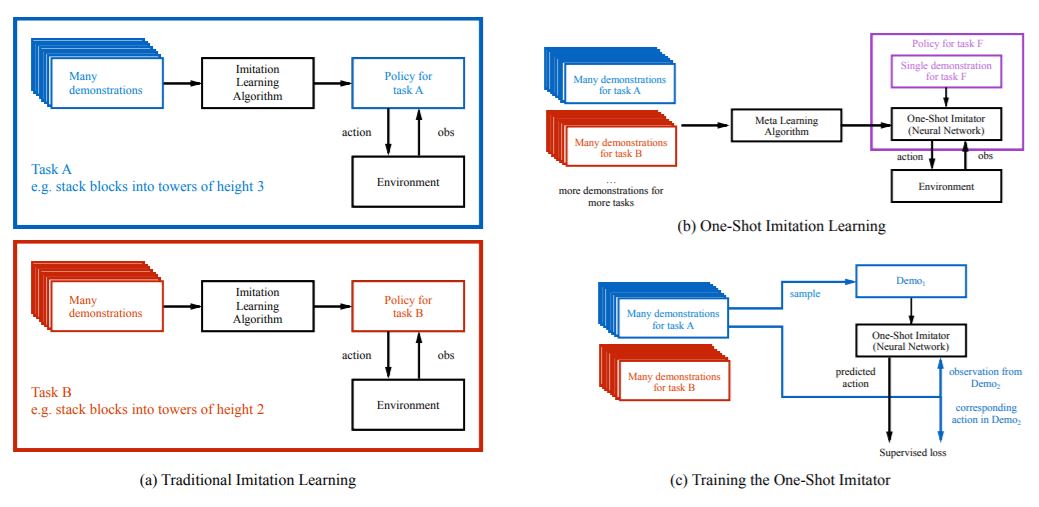
Robotic systems can be used for many applications, but to truly be useful for complex applications, they need to overcome 2 challenges: having the intent of the task at hand communicated to them, and being able to perform the manipulations necessary to complete this task. It is preferable to use demonstration to teach the robotic systems rather than natural language, as natural language may often fail to convey the details and intricacies required for the task. However, current work on learning from demonstrations is only successful with large amounts of feature engineering or a large number of demonstrations. The proposed model aims to achieve 'one-shot' imitation learning, ie. learning to complete a new task from just a single demonstration of it without any other supervision. As input, the proposed model takes the observation of the current instance a task, and a demonstration of successfully solving a different instance of the same task. Strong generalization was achieved by using a soft attention mechanism on both the sequence of actions and states that the demonstration consists of, as well as on the vector of element locations within the environment. The success of this proposed model at completing a series of block stacking tasks can be viewed at http://bit.ly/nips2017-oneshot.

One-Shot Imitation Learning

Problem Formalization

The problem is briefly formalized with the authors describing a distribution of tasks, an individual task, a distribution of demonstrations for this task, and a single demonstration respecitvely as \[T, t\sim T, D(t), d\sim D(t)\] In addition, an action, an observation, parameters, and a policy are respectively defined as \[a, o, \theta, \pi_\theta(a|o,d)\] In particular, a demonstration is a sequence of observation and action pairs \[d = [(o_1, a_1),(o_2, a_2), . . . ,(o_T , a_T )]\] Assuming that $$T$$ and some evaluation function $$R_t(d): R^T \rightarrow R$$ are given, and that succesful demonstrations are available for each task, then the objective is to maximize expectation of the policy performance over \[t\sim T, d\sim D(t)\].

Block Stacking Tasks

The tasks that the authors focus on is block stacking. A user specifies in what final configuration cubic blocks should be stacked, and the goal is to use a 7-DOF Fetch robotic arm to arrange the blocks in this configuration. The number of blocks, and their desired configuration (ie. number of towers, the height of each tower, and order of blocks within each tower) can be varied and encoded as a string. For example, 'abc def' would signify 2 towers of height 3, with block A on block B on block C in one tower, and block D on block E on block F in a second tower. To add complexity, the initial configuration of the blocks can vary and is encoded as a set of 3-dimensional vectors describing the position of each block relative to the robotic arm.

Algorithm

To avoid needing to specify a reward function, the authors use behavioral cloning and DAGGER, 2 imitation learning methods that require only demonstrations, for training. In each training step, a list of tasks is sampled, and for each, a demonstration with injected noise along with some observation-action pairs are sampled. Given the current observation and demonstration as input, the policy is trained against the sampled actions by minimizing L2 norm for continuous actions, and cross-entropy for discrete ones. Adamax is used as the optimizer with a learning rate of 0.001.

Architecture

The authors propose a novel architecture for imitation learning, consisting of 3 networks.

Manipulation network