STAT946F17/ Coupled GAN

Introduction

Generative models attempt to characterize and estimate the underlying probability distribution of the data (typically images) and in doing so generate samples from the aforementioned learned distribution. Moment-matching generative networks, Variational auto-encoders, and Generative Adversarial Networks (GANs) are some of the most popular (and recent) class of techniques in this burgeoning literature on generative models. The authors of the paper we are reviewing focus on proposing an extension to the class of GANs.

The novelty of the proposed Coupled GAN (CoGAN) method lies in extending the GAN procedure (described in the next section) to the multi-domain setting. That is, the CoGAN methodology attempts to learn the (underlying) joint probability distribution of multi-domain images as a natural extension from the marginal setting associated with the vanilla GAN framework. Given the dense and active literature on generative models, generating images in multiple domains in far from ground breaking. Related works revolve around multi-modal learning including multi-modal deep learning, semi-coupled dictionary learning, joint embedding space learning, cross-domain image generation to name a few \TODO{inline citations}. Thus, the novelty of the author's contributions to this field comes from two key differentiating points. Firstly, this was (one of) the first papers to endeavor to generate multi-domain images with the GAN framework. Secondly, and perhaps more significantly, the authors proposed to learn the underlying joint distribution without requiring the presence of tuples of corresponding images in the training set. Only sets of images drawn from the (marginal) distributions of the separate domains is sufficient. As per the authors' claim constructing tuples of corresponding images to train from is challenging and a potential bottle-neck for multi-domain image generation. One way around this bottleneck is thus to use their proposed CoGAN methodology. More details of how the author's achieve joint-distribution learning will be provided in the Coupled GAN section below.

Generative Adversarial Networks

A typical GAN framework consists of a generative model and a discriminative model. The generative model, which often is a de-convolutional network, takes as input a random latent vector (typically uniform or Gaussian), and synthesizes novel images resembling the real images (training set). The discriminative model, often a convolutional network, on the other hand tries to distinguish between the fake synthesized images and the real images. The idea then is to let the two component models of the GAN framework "compete" with each other in the form of a minmax two player game.

To further clarify and fix this idea, we introduce the mathematical setup of GANs following the notation used by the authors of this paper for sake of consistency. Let us define the following in our setup:

[math]\displaystyle{ \mathbf{x}- }[/math] natural image drawn from underlying distribution [math]\displaystyle{ p_X }[/math],

[math]\displaystyle{ \mathbf{z} \sim U[-1,1]^d- }[/math] a latent random vector,

$g-$ generative model, $f-$ discriminative model.

Ideally we are aiming for the system of these two adversarial networks to behave as:

Generator: $g(\mathbf{z})$ outputs an image with same support as $\mathbf{x}$. The probability density of the images output by $g$ can be denoted by $p_G$,

Discriminator: $f(\mathbf{x})=1$ if $\mathbf{x} \sim p_X$ and $f(\mathbf{x})=0$ if $\mathbf{x} \sim p_G$.

To train such a system of networks given our goal,i.e $p_G \rightarrow p_X$, we must treat such a framework as the following minmax two player game:

$\displaystyle \max_{g}$ $\min\limits_{f} V(g,f) = \mathop{\mathbb{E}}_{\mathbf{x} \sim p_X}[-\log(f(\mathbf{x}))] + \mathop{\mathbb{E}}_{\mathbf{z} \sim p_{Z}(\mathbf{z})}[-\log(1-f(g(\mathbf{z})))] $.

See Goodfellow et al.2014, the seminal paper on this topic, for more information.

Coupled Generative Adversarial Networks

The overarching goal of this framework is to learn a joint distribution of multi-domain images from data. That is, a density value is assigned to each joint occurrence of images in different domains. Examples of such pair of images in different domains include images of a particular scene with different modalities (color and depth) or images of the same face but with different facial attributes.

To this end, the CoGAN setup consists of a pair of GANs, denoted as $GAN_1$ and $GAN_2$. Each GAN is tasked with synthesizing images in one domain. A naive training of such a system will result in learning the product of the two marginal distributions i.e independence. However, by forcing the two GANs to share weights, the authors were able to demonstrate that they could in some sense learn the joint distribution of images. We will now describe the details of the generator and discriminator components of the setup and conclude this section with a summary of CoGAN learning algorithm.

Generator Models

Suppose $\mathbf{x_1} \sim p_{X_1}$ and $\mathbf{x_2} \sim p_{X_2}$ denote the natural images being drawn from the two marginal distributions of domain 1 and domain 2. Further, let $g_1$ be the generator of $GAN_1$ and $g_2$ be the generator of $GAN_2$. Both these generators take the as input the latent vector $\mathbf{z}$ as defined in the previous section as input and out images in their specific domains. For completeness, denote the distributions of $g_1(\mathbf{z})$ and $g_2(\mathbf{z})$ as $p_{G_1}$ and $p_{G_2}$ respectively. We can characterize these two generator models as multi-layer perceptrons in the following way:

\begin{align*} g_1(\mathbf{z})=g_1^{(m_1)}(g_1^{(m_1 -1)}(\dots g_1^{(2)}(g_1^{(1)}(\mathbf{z})))), \quad g_2(\mathbf{z})=g_2^{(m_2)}(g_2^{(m_2-1)}(\dots g_2^{(2)}(g_2^{(1)}(\mathbf{z})))), \end{align*} where $g_1^{(i)}$ an $g_2^{(i)}$ are the $i^{th}$ layers of $g_1$ and $g_2$ which respectively have a total of $m_1$ and $m_2$ layers each. Note $m_1$ need not be the same as $m_2$.

As the generator networks can be thought of as a inverse of the prototypical convolutional networks (just as an example), the layers of these generator networks gradually decodes information from high-level abstract concepts to low-level details(last few layers). Taking this idea as the blueprint for the inner-workings of generator networks, the author's hypothesize that corresponding images in two domains share the same high-level semantics but with differing lower-level details. To put this hypothesis to practice, they forced the first $k$ layers of $g_1$ and $g_2$ to have identical structures and share the same weights. That is, $\mathbf{\theta}_{g_1^{(i)}}=\mathbf{\theta}_{g_2^{(i)}}$ for $i=1,\dots,k$ where $\mathbf{\theta}_{g_1^{(i)}}$ and $\mathbf{\theta}_{g_1^{(i)}}$ represents the parameters of the layers $g_1^{(i)}$ and $g_2^{(i)}$ respectively. Hence the two generator networks share the starting $k$ of the deep network and have different last layers to decode the differing material details in each domain.

Discriminative Models

Suppose $f_1$ and $f_2$ are the respective discriminative models of the two GANs. These models can be characterized by \begin{align*} f_1(\mathbf{x}_1)=f_1^{(n_1)}(f_1^{(n_1 -1)}(\dots f_1^{(2)}(f_1^{(1)}(\mathbf{x}_1)))), \quad f_2(\mathbf{x}_2)=f_2^{(n_2)}(f_2^{(n_2-1)}(\dots f_2^{(2)}(f_2^{(1)}(\mathbf{x}_1)))), \end{align*} where $f_1^{(i)}$ an $f_2^{(i)}$ are the $i^{th}$ layers of $f_1$ and $f_2$ which respectively have a total of $n_1$ and $n_2$ layers each. Note $n_1$ need not be the same as $n_2$. In contrast to generator models, the first layers of $f_1$ and $f_2$ extract the lower level details where the last layers extract the abstract higher level details. To reflect the prior hypothesis of shared higher level semantics between corresponding images, we can force $f_1$ and $f_2$ to now share the weights for last $l$ layers. That is, $\mathbf{\theta}_{f_1^{(n_1-i)}}=\mathbf{\theta}_{f_2^{(n_2-i)}}$ for $i=0,\dots,l-1$ where $\mathbf{\theta}_{f_1^{(i)}}$ and $\mathbf{\theta}_{f_1^{(i)}}$ represents the parameters of the layers $f_1^{(i)}$ and $f_2^{(i)}$ respectively.

Coupled GAN (CoGAN) Framework and Learning

The following figure taken from the paper summarizes the system of models described in the previous subsections.

The CoGAN framework can be expressed as the following constrained min-max game

\begin{align*} \max\limits_{g_1,g_2} \min\limits_{f_1, f_2} V(f_1,f_2,g_1,g_2)\quad \text{subject to} \ \mathbf{\theta}_{g_1^{(i)}}=\mathbf{\theta}_{g_2^{(i)}}, i=1,\dots k, \quad \mathbf{\theta}_{f_1^{(n_1-j)}}=\mathbf{\theta}_{f_2^{(n_2-j)}}, j=1,\dots,l-1, \end{align*} where the value function V is characterized as \begin{align*} \mathop{\mathbb{E}}_{\mathbf{x}_1 \sim p_{X_1}}[-\log(f_1(\mathbf{x_1}))] + \mathop{\mathbb{E}}_{\mathbf{z} \sim p_{Z}(\mathbf{z})}[-\log(1-f_1(g_1(\mathbf{z})))]+\mathop{\mathbb{E}}_{\mathbf{x}_2 \sim p_{X_2}}[-\log(f_2(\mathbf{\mathbf{x}_2}))] + \mathop{\mathbb{E}}_{\mathbf{z} \sim p_{Z}(\mathbf{z})}[-\log(1-f_2(g_2(\mathbf{z})))]. \end{align*}

For the purposes of story telling, we can describe this game has having two teams with two players each. The generative models are in the same team and collaborate with each other to synthesize a pair of images in two different domains with goal of fooling the discriminative models. The discriminative models then with collaboration try to differentiate between images drawn from the training data in their respective domains and the images generated by the respective generative models. The training algorithm for the CoGAN that was used is described in the following figure.

Experiments

To begin with, note that the authors do not use corresponding images in the training set in accordance with the goal of learning the joint distribution of multi-domain images without correspondance supervision. As at the time the paper was written, there were no existing approached with identical prerogatives (i.e training with no correspondance supervision), they compared CoGAN with conditional GAN (see \cite{conditionalGAN} for more details on conditional GAN).

MNIST Dataset

The MNIST training set was experimented with for two tasks:

1. Task A: Learning a joint distribution of a digit and its edge image.
2. Task B: Learning a joint distribution of a digit and its negative image.

For the generative models, the authors used convolutional networks with 5 identical layers. They varied the number of shared layers as part of their experimental setup. The two discriminative models were a version of the LeNet (\TODO{cite relevant}). The results of the CoGAN generation scheme are displayed in the figure below.

As you can see from the figure above, the CoGAN system was able to generate pairs of corresponding images without explicitly training with correspondance supervision. This was naturally due to sharing weights in lower levels used for decoding high-level semantics. Without sharing these weights, the CoGAN would just output a pair of unrelated images in the two domains.

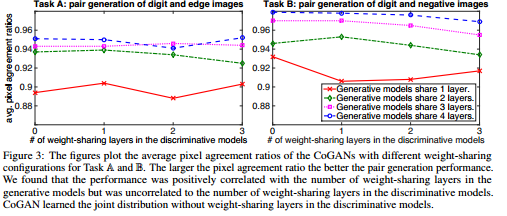
To investigate the effects of weight sharing in the generator/discriminator models used for both tasks, the authors varied the number of shared levels. To quantify the performance of the generator, the image generated by $GAN_1$ (domain 1) was transformed to the 2nd domain using the same method used to generate training images in the 2nd domain. Then this transformed image was compared with the image generated by $GAN_2$. Naturally, if the joint distribution was learned completely, these two images would be identical. With that goal in mind, the authors used pixel agreement ratios for 10000 images as the evaluation metric. In particular, 5 trails with different weight initializations were used and an average pixel agreement ratio was taken. The results depicting the relationship between the average pixel agreement ratio and number of shared layers is summarized in the figure below.

The results naturally offered some corroboration to our intuitions. The more number of shared layers in the generator models. the higher the pixel agreement ratios. Interestingly the number of shared layers in the discriminative model does not seem to affect the pixel agreement ratios. Note this is a pretty naive and toy example as we by nature of the evaluation criteria have a deterministic way of generating imaged in the 2nd domain.

Finally for this example, the authors compared the CoGAN framework with the conditional GAN model. For the conditional GAN, the generative and discriminative models were identical to those used for the CoGAN results. The conditional GAN additionally took a binary variable (the conditioning variable) as input. When the binary variable was 0, the conditional GAN synthesized an image in domain 1 and when it was 1 an image in domain 2. Naturally for fair comparison, the training set did not already contain corresponding pairs of images. The experiments were conducted for the two tasks described above and the pixel agreement ratio (PAR) was the evaluation criteria. For Task A, the CoGAN resulted in a PAR of 0.952 in comparison with 0.909 for the conditional GAN. For Task B, the CoGAN resulted in a PAR of 0.967 compared with a PAR of 0.778 for the conditional GAN. The results are not particularly eye opening as the CoGAN was more specifically designed for purpose of learning the joint distribution of multi-domain images whereas these tasks are just a very niche application for the conditional GAN. Nevertheless, for Task B, the results look promising.

References and Supplementary Resources

I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio. Generative adversarial nets. In NIPS, 2014.