Meta-Learning For Domain Generalization: Difference between revisions
(→Method) |
|||
| Line 10: | Line 10: | ||
== Method == | == Method == | ||
In the DG setting, we assume there are S source domains <math> S </math> and T target domains <math> T </math> . We define a single model parametrized as <math> \theta </math> to solve the specified task. DG aims for training <math> \theta </math> on the source domains, such that it generalizes to the target domains. At each learning iteration we split the original S source domains <math> S </math> into S−V meta-train domains <math> \bar{S} </math> and V meta-test domains <math> \breve{S} </math> (virtual-test domain). This is to mimic real train-test domain-shifts so that over many iterations we can train a model to achieve good generalization in the final-test evaluated on target domains T . | In the DG setting, we assume there are S source domains <math> S </math> and T target domains <math> T </math> . We define a single model parametrized as <math> \theta </math> to solve the specified task. DG aims for training <math> \theta </math> on the source domains, such that it generalizes to the target domains. At each learning iteration we split the original S source domains <math> S </math> into S−V meta-train domains <math> \bar{S} </math> and V meta-test domains <math> \breve{S} </math> (virtual-test domain). This is to mimic real train-test domain-shifts so that over many iterations we can train a model to achieve good generalization in the final-test evaluated on target domains <math>T</math> . | ||
The paper explains the method based on two approaches; Supervised Learning and Reinforcement Learning. | The paper explains the method based on two approaches; Supervised Learning and Reinforcement Learning. | ||
| Line 20: | Line 20: | ||
==== Meta-Train ==== | ==== Meta-Train ==== | ||
The model is updated on S-V domains <math> \bar{S} </math> and the loss function is defined as: <math> F(.) = \frac{1}{S-V} \sum\limits_{i=1}^{S-V} \frac {1}{N_i} \sum\limits_{j=1}^{N_i} l_{\theta}(\hat{y}_j^{(i)}, y_j^{(i)})</math> | The model is updated on S-V domains <math> \bar{S} </math> and the loss function is defined as: <math> F(.) = \frac{1}{S-V} \sum\limits_{i=1}^{S-V} \frac {1}{N_i} \sum\limits_{j=1}^{N_i} l_{\theta}(\hat{y}_j^{(i)}, y_j^{(i)})</math> | ||
In this step the model is optimized by gradient descent like follows: <math> \theta^{\prime} = \theta - \alpha \nabla_{\theta} </math> | In this step the model is optimized by gradient descent like follows: <math> \theta^{\prime} = \theta - \alpha \nabla_{\theta} </math> | ||
| Line 26: | Line 27: | ||
In each mini-batch the model is also virtually evaluated on the V meta-test domains <math>\breve{S}</math>. This meta-test evaluation simulates testing on new domains with different statistics, in order to allow learning to generalize across domains. The loss for the adapted parameters calculated on the meta-test domains is as follows: <math> G(.) = \frac{1}{V} \sum\limits_{i=1}^{V} \frac {1}{N_i} \sum\limits_{j=1}^{N_i} l_{\theta^{\prime}}(\hat{y}_j^{(i)}, y_j^{(i)})</math> | In each mini-batch the model is also virtually evaluated on the V meta-test domains <math>\breve{S}</math>. This meta-test evaluation simulates testing on new domains with different statistics, in order to allow learning to generalize across domains. The loss for the adapted parameters calculated on the meta-test domains is as follows: <math> G(.) = \frac{1}{V} \sum\limits_{i=1}^{V} \frac {1}{N_i} \sum\limits_{j=1}^{N_i} l_{\theta^{\prime}}(\hat{y}_j^{(i)}, y_j^{(i)})</math> | ||
The loss on the meta-test domain is calculated using the updated parameters <math>\theta' </math> from meta-train. This means that for optimization with respect to <math>G </math> we will need the second derivative with respect to <math>\theta </math>. | |||
==== Final Objective Function ==== | ==== Final Objective Function ==== | ||
Combining the two loss functions, the final objective function is as follows: <math> argmin_{\theta} \; F(\theta) + \beta G(\theta - \alpha F^{\prime}(\theta)) </math>. Algorithm 1 illustrates the supervised learning approach. | Combining the two loss functions, the final objective function is as follows: <math> argmin_{\theta} \; F(\theta) + \beta G(\theta - \alpha F^{\prime}(\theta)) </math>, where <math>\beta</math> represents how much meta-test weighs. Algorithm 1 illustrates the supervised learning approach. | ||
[[File:ashraf1.jpg |center|600px]] | [[File:ashraf1.jpg |center|600px]] | ||
Revision as of 20:22, 16 November 2020
Presented by
Parsa Ashrafi Fashi
Introduction
Domain Shift problem addresses the problem where a model trained on a data distribution cannot perform well when tested on another domain with a different distribution. Domain Generalization tries to tackle this problem by producing models that can perform well on unseen target domains. Several approaches have been adapted for the problem, such as training a model for each source domain, extracting a domain agnostic representation, and semantic feature learning. Meta-Learning and specifically Model-Agnostic Meta-Learning models, which have been widely adopted recently, are models capable of adapting or generalizing to new tasks and new environments that have never been encountered during training time. Meta-learning is also known as "learning to learn". It aims to enable intelligent agents to take the principles they learned in one domain and apply them to other domains. One concrete meta-learning task is to create a game bot who can quickly master a new game. Hereby defining tasks as domains, the paper tries to overcome the problem in a model-agnostic way.
Previous Work
There were 3 common approaches to Domain Generalization. The simplest way is to train a model for each source domain and estimate which model performs better on a new unseen target domain [1]. A second approach is to presume that any domain is composed of a domain-agnostic and a domain-specific component. By factoring out the domain-specific and domain-agnostic component during training on source domains, the domain-agnostic component can be extracted and transferred as a model that is likely to work on a new source domain [2]. Finally, a domain-invariant feature representation is learnt to minimize the gap between multiple source domains and it should provide a domain-independent representation that performs well on a new target domain [3][4][5].
Method
In the DG setting, we assume there are S source domains [math]\displaystyle{ S }[/math] and T target domains [math]\displaystyle{ T }[/math] . We define a single model parametrized as [math]\displaystyle{ \theta }[/math] to solve the specified task. DG aims for training [math]\displaystyle{ \theta }[/math] on the source domains, such that it generalizes to the target domains. At each learning iteration we split the original S source domains [math]\displaystyle{ S }[/math] into S−V meta-train domains [math]\displaystyle{ \bar{S} }[/math] and V meta-test domains [math]\displaystyle{ \breve{S} }[/math] (virtual-test domain). This is to mimic real train-test domain-shifts so that over many iterations we can train a model to achieve good generalization in the final-test evaluated on target domains [math]\displaystyle{ T }[/math] .
The paper explains the method based on two approaches; Supervised Learning and Reinforcement Learning.
Supervised Learning
First, [math]\displaystyle{ l(\hat{y},y) }[/math] is defined as a cross-entropy loss function. ( [math]\displaystyle{ l(\hat{y},y) = -\hat{y}log(y) }[/math]). The process is as follows.
Meta-Train
The model is updated on S-V domains [math]\displaystyle{ \bar{S} }[/math] and the loss function is defined as: [math]\displaystyle{ F(.) = \frac{1}{S-V} \sum\limits_{i=1}^{S-V} \frac {1}{N_i} \sum\limits_{j=1}^{N_i} l_{\theta}(\hat{y}_j^{(i)}, y_j^{(i)}) }[/math]
In this step the model is optimized by gradient descent like follows: [math]\displaystyle{ \theta^{\prime} = \theta - \alpha \nabla_{\theta} }[/math]
Meta-Test
In each mini-batch the model is also virtually evaluated on the V meta-test domains [math]\displaystyle{ \breve{S} }[/math]. This meta-test evaluation simulates testing on new domains with different statistics, in order to allow learning to generalize across domains. The loss for the adapted parameters calculated on the meta-test domains is as follows: [math]\displaystyle{ G(.) = \frac{1}{V} \sum\limits_{i=1}^{V} \frac {1}{N_i} \sum\limits_{j=1}^{N_i} l_{\theta^{\prime}}(\hat{y}_j^{(i)}, y_j^{(i)}) }[/math]
The loss on the meta-test domain is calculated using the updated parameters [math]\displaystyle{ \theta' }[/math] from meta-train. This means that for optimization with respect to [math]\displaystyle{ G }[/math] we will need the second derivative with respect to [math]\displaystyle{ \theta }[/math].
Final Objective Function
Combining the two loss functions, the final objective function is as follows: [math]\displaystyle{ argmin_{\theta} \; F(\theta) + \beta G(\theta - \alpha F^{\prime}(\theta)) }[/math], where [math]\displaystyle{ \beta }[/math] represents how much meta-test weighs. Algorithm 1 illustrates the supervised learning approach.

Reinforcement Learning
In application to the reinforcement learning (RL) setting, we now assume an agent with a policy [math]\displaystyle{ \pi }[/math] that inputs states [math]\displaystyle{ s }[/math] and produces actions [math]\displaystyle{ a }[/math] in a sequential decision making task: [math]\displaystyle{ a_t = \pi_{\theta}(s_t) }[/math]. The agent operates in an environment and its goal is to maximize its discounted return, [math]\displaystyle{ R = \sum\limits_{t} \delta^t R_t(s_t, a_t) }[/math] where [math]\displaystyle{ R_t }[/math] is the reward obtained at timestep [math]\displaystyle{ t }[/math] under policy [math]\displaystyle{ \pi }[/math] and [math]\displaystyle{ \delta }[/math] is the discount factor. Here, tasks map to return functions and domains map to different environments.
Meta-Train
In meta-training, the loss function [math]\displaystyle{ F(·) }[/math]now corresponds to the negative discounted return [math]\displaystyle{ -R }[/math] of policy [math]\displaystyle{ \pi_{\theta} }[/math], averaged over all the meta-training environments in [math]\displaystyle{ \bar{S} }[/math]. That is, \begin{align} F = \frac{1}{|\bar{S}|} \sum_{s \in \bar{S}} -R_s \end{align}
Then the optimal policy is obtained by minimizing [math]\displaystyle{ F }[/math].
Meta-Test
The step is like a meta-test of supervised learning and loss is again negative of return function. For RL calculating this loss requires rolling out the meta-train updated policy [math]\displaystyle{ \theta }[/math] in the meta-test domains to collect new trajectories and rewards. The reinforcement learning approach is also illustrated completely in algorithm 2.

Alternative Variants of MLDG
The authors propose different variants of MLDG objective function. For example the so-called MLDG-GC is one that normalizes the gradients upon update to compute the cosine similarity. It is given by: \begin{equation} \text{argmin}_\theta F(\theta) + \beta G(\theta) - \beta \alpha \frac{F'(\theta) \cdot G'(\theta)}{||F'(\theta)||_2 ||G'(\theta)||_2}. \end{equation}
Another one stops the update of the parameters after the meta-train has converged. This intuition gives the following objective function called MLDG-GN: \begin{equation} \text{argmin}_\theta F(\theta) - \beta ||G'(\theta) - \alpha F'(\theta)||_2^2 \end{equation}.
Experiments
The Proposed method is exploited in 4 different experiment results (2 supervised and 2 reinforcement learning experiments).
Illustrative Synthetic Experiment
In this experiment, nine domains by sampling curved deviations are synthesized from a diagonal line classifier. We treat eight of these as sources for meta-learning and hold out the last for the final-test. Fig. 1 shows the nine synthetic domains which are related in form but differ in the details of their decision boundary. The results show that MLDG performs near perfect and the baseline model without considering domains overfits in the bottom left corner.

Object Detection
For object detection, the PACS multi-domain recognition benchmark is exploited; a dataset designed for the cross-domain recognition problems .This dataset has 7 categories (‘dog’, ‘elephant’, ‘giraffe’, ‘guitar’, ‘house’, ‘horse’ and ‘person’) and 4 domains of different stylistic depictions (‘Photo’, ‘Art painting’, ‘Cartoon’ and ‘Sketch’). The diverse depiction styles provide a significant domain gap. The Result of the Current approach compared to other approaches is presented in Table 1. The baseline models are D-MTAE[5],Deep-All (Vanilla AlexNet)[2], DSN[6]and AlexNet+TF[2]. On average, the proposed method outperforms other methods.

Cartpole
The objective is to balance a pole upright by moving a cart. The action space is discrete – left or right. The state has four elements: the position and velocity of the cart and the angular position and velocity of the pole. There are two sub-experiments designed. In the first one, the domain factor is varied by changing the pole length. They simulate 9 domains with pole lengths. In the second they vary multiple domain factors – pole length and cart mass. In both experiments, we randomly choose 6 source domains for training and hold out 3 domains for (true) testing. Since the game can last forever, if the pole does not fall, we cap the maximum steps to 200. The result of both experiments are presented in Tables 2 and 3. The baseline methods are RL-All (Trains a single policy by aggregating the reward from all six source domains) RL-Random-Source (trains on a single randomly selected source domain) and RL-undo-bias: Adaptation of the (linear) undo-bias model of [7]. The proposed MLDG outperforms the baselines.


Mountain Car
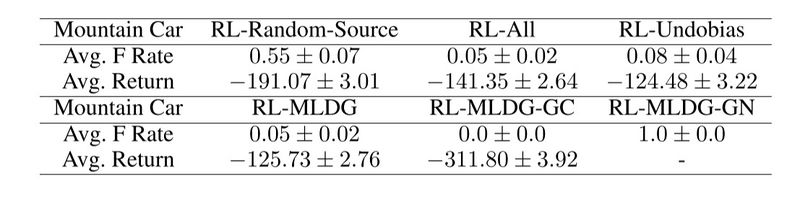
In this classic RL problem, a car is positioned between two mountains, and the agent needs to drive the car so that it can hit the peak of the right mountain. The difficulty of this problem is that the car engine is not strong enough to drive up the right mountain directly. The agent has to figure out a solution of driving up the left mountain to first generate momentum before driving up the right mountain. The state observation in this game consists of two elements: the position and velocity of the car. There are three available actions: drive left, do nothing, and drive right. Here the baselines are the same as Cartpole. The model doesn't outperform the RL-undo-bias but has a close return value. The results are shown in Table 4.
Conclusion
This paper proposed a model-agnostic approach to domain generalization unlike prior model-based domain generalisation approaches which it scales well with the number of domains and it can also be applied to different Neural Network models. Experimental evaluation shows state-of-the-art results on a recent challenging visual recognition benchmark and promising results on multiple classic RL problems.
Critiques
I believe that meta learning-based approach (MLDG) extending MAML to the domain generalization problem might have some limitation problems. The objective function of MAML is more applicable for fast task adaptation even it can be shown from the presented tasks in the paper. Also, in the generalization, we do not have access to samples from a new domain, so the MAML-like objective might lead to sub-optimal, as it is highly abstracted from the feature representations. In addition to this, it is hard to scale MLDG to deep architectures like Resnet as it requires differentiating through k iterations of optimization updates, which will lead to some limitations, so I would believe it will be more effective in task networks as it is much shallower than the feature networks.
References
[1]: [Xu et al. 2014] Xu, Z.; Li, W.; Niu, L.; and Xu, D. 2014. Exploiting low-rank structure from latent domains for domain generalization. In ECCV.
[2]: [Li et al. 2017] Li, D.; Yang, Y.; Song, Y.-Z.; and Hospedales, T. 2017. Deeper, broader and artier domain generalization. In ICCV.
[3]: [Muandet, Balduzzi, and Scholkopf 2013] ¨ Muandet, K.; Balduzzi, D.; and Scholkopf, B. 2013. Domain generalization via invariant feature representation. In ICML.
[4]: [Ganin and Lempitsky 2015] Ganin, Y., and Lempitsky, V. 2015. Unsupervised domain adaptation by backpropagation. In ICML.
[5]: [Ghifary et al. 2015] Ghifary, M.; Bastiaan Kleijn, W.; Zhang, M.; and Balduzzi, D. 2015. Domain generalization for object recognition with multi-task autoencoders. In ICCV.
[6]: [Bousmalis et al. 2016] Bousmalis, K.; Trigeorgis, G.; Silberman, N.; Krishnan, D.; and Erhan, D. 2016. Domain separation networks. In NIPS.
[7]: [Khosla et al. 2012] Khosla, A.; Zhou, T.; Malisiewicz, T.; Efros, A. A.; and Torralba, A. 2012. Undoing the damage of dataset bias. In ECCV.