stat841

Classfication-2009.9.30

Classification

In classification we attempt to approximate a function [math]\displaystyle{ h }[/math], by using a training data set, that will then be able to accurately classify new data inputs.

Given,
[math]\displaystyle{ \mathcal{X} \subset \mathbb{R}^{d} }[/math], a subset of the D-dimensional real vectors and
[math]\displaystyle{ \mathcal{Y} }[/math], a finite set of labels

We try to determine a 'classification rule' [math]\displaystyle{ h }[/math] such that,

[math]\displaystyle{ \,h: \mathcal{X} \mapsto \mathcal{Y} }[/math]

We use n ordered pairs of training data to approximate [math]\displaystyle{ h }[/math],
[math]\displaystyle{ \,\{(X_{1},Y_{1}), (X_{2},Y_{2}), \dots , (X_{n},Y_{n})\} }[/math], [math]\displaystyle{ \,X_{i} \in \mathcal{X} }[/math],[math]\displaystyle{ \,Y_{i} \in \mathcal{Y} }[/math].

Thus, given a new input,
[math]\displaystyle{ \,X \in \mathcal{X} }[/math]
by using the classification rule we can predict a corresponding [math]\displaystyle{ \,\hat{Y}=h(X) }[/math]

Example Suppose we wish to classify fruit into apples and oranges by considering certain features of the fruit. Let [math]\displaystyle{ \mathcal{X}_{i} }[/math]= (colour, diameter, weight) for fruit i and [math]\displaystyle{ \mathcal{Y} }[/math]={apple, orange}. The goal is to find a classification rule such that when a new fruit [math]\displaystyle{ \mathcal{X} }[/math] is presented, it can be classified as either an apple or an orange.

Error rate

'True error rate' of a classifier(h) is defined as the probability that [math]\displaystyle{ \hat{Y} }[/math] predicted from [math]\displaystyle{ \,X }[/math] by classifier [math]\displaystyle{ \,h }[/math] does not actually equal to [math]\displaystyle{ \,Y }[/math], namely, [math]\displaystyle{ \, L(h)=P(h(X) \neq Y) }[/math].

'Empirical error rate(training error rate)' of a classifier(h) is defined as the frequency that [math]\displaystyle{ \hat{Y} }[/math] predicted from [math]\displaystyle{ \,X }[/math] by [math]\displaystyle{ \,h }[/math] does not equal [math]\displaystyle{ \,Y }[/math] in n predictions. The mathematical expression is:

[math]\displaystyle{ \, L_{h}= \frac{1}{n} \sum_{i=1}^{n} I(h(X_{i}) \neq Y_{i}) }[/math], where [math]\displaystyle{ \,I }[/math] is an indicator that [math]\displaystyle{ \, I= \left\{\begin{matrix} 1 & h(X_i) \neq Y_i \\ 0 & h(X_i)=Y_i \end{matrix}\right. }[/math].

Bayes Classifier

The principle of Bayes Classifier is to calculate posteriori probability of given object from its priors probability via Bayes formula, and then choose the class with biggest posteriori probability as the one what the object affiliated with.
Mathematically, for k classes and given object [math]\displaystyle{ \,X=x }[/math], we are going to find out [math]\displaystyle{ \,y_{i} }[/math] that [math]\displaystyle{ \,P(Y=y_{i}|X=x)=max \{ P(Y=y|X=x), y \in \mathcal{Y} \} }[/math], and classify [math]\displaystyle{ \,X }[/math] into class [math]\displaystyle{ \,y_{i} }[/math]. In order to calculate the value of [math]\displaystyle{ \,P(Y=y_{i}|X=x) }[/math], we use the Bayes formula:
[math]\displaystyle{ \,P(Y=y|X=x)=\frac{P(X=x|Y=y)P(Y=y)}{P(X=x)}=\frac{P(X=x|Y=y)P(Y=y)}{\Sigma_{\forall y \in \mathcal{Y}}P(X=x|Y=y)P(Y=y)} }[/math]
where [math]\displaystyle{ \,P(Y=y|X=x) }[/math] is referred to as the posteriori probability, [math]\displaystyle{ \,P(Y=y) }[/math] as the priors probability, [math]\displaystyle{ \,P(X=x|Y=y) }[/math] as the likelihood, and [math]\displaystyle{ \,P(X=x) }[/math] as the evidence.

For the special case that [math]\displaystyle{ \,Y }[/math] has only two possible values, that is, [math]\displaystyle{ \, \mathcal{Y}=\{0, 1\} }[/math]. Consider the probability that [math]\displaystyle{ \,r(X)=P\{Y=1|X=x\} }[/math]. Given [math]\displaystyle{ \,X=x }[/math], By Bayes formula, we have

[math]\displaystyle{ \,r(X)=P(Y=1|X=x)=\frac{P(X=x|Y=1)P(Y=1)}{P(X=x)}=\frac{P(X=x|Y=1)P(Y=1)}{P(X=x|Y=1)P(Y=1)+P(X=x|Y=0)P(Y=0)} }[/math]

Definition:

The Bayes classification rule [math]\displaystyle{ \,h }[/math] is:

[math]\displaystyle{ \, h(X)= \left\{\begin{matrix} 1 & r(x)\gt \frac{1}{2} \\ 0 & otherwise \end{matrix}\right. }[/math]

The set [math]\displaystyle{ \,D(h)=\{x: P(Y=1|X=x)=P(Y=0|X=x)\} }[/math] is called the decision boundary.

'Important Theorem': The Bayes rule is optimal in true error rate, that is for any other classification rule [math]\displaystyle{ \, \overline{h} }[/math], we have [math]\displaystyle{ \,L(\overline{h}) \le L(h) }[/math].

Example:
We’re going to predict if a particular student will pass STAT441/841. We have data on past student performance. For each student we know: If student’s GPA > 3.0 (G) If student had a strong math background (M) If student is a hard worker (H) If student passed or failed course

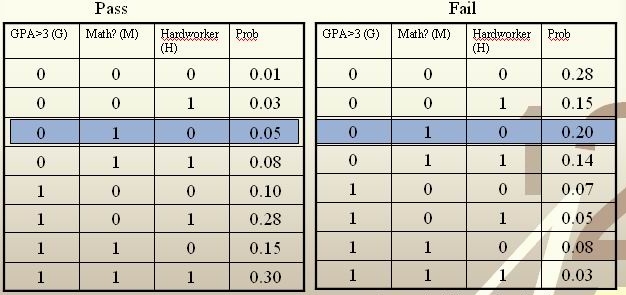
[math]\displaystyle{ \, \mathcal{Y}= \{ 0,1 \} }[/math], where 1 refers to pass and 0 refers to fail. Assume that [math]\displaystyle{ \,P(Y=1)=P(Y=0)=0.5 }[/math]
For a new student comes along with values [math]\displaystyle{ \,G=0, M=1, H=0 }[/math], we calculate [math]\displaystyle{ \,r(X)=P(Y=1|X=(0,1,0)) }[/math] as

[math]\displaystyle{ \,r(X)=P(Y=1|X=(0,1,0))=\frac{P(X=(0,1,0)|Y=1)P(Y=1)}{P(X=(0,1,0)|Y=1)P(Y=1)+P(X=(0,1,0)|Y=0)P(Y=0)}=\frac{0.025}{0.125}=0.2\lt \frac{1}{2} }[/math]
Thus, we classify the new student into class 0, namely, we predict him to fail in this course.

Notice: Although the Bayes rule is optimal, we still need other methods, and the reason for the fact is that in the Bayes equation discussed before, it is generally impossible for us to know the [math]\displaystyle{ \,P(Y=1) }[/math], and [math]\displaystyle{ \,P(X=x|Y=1) }[/math] and ultimately calculate the value of [math]\displaystyle{ \,r(X) }[/math], which makes Bayes rule inconvenient in practice.

Currently, there are four primary classifier based on Bayes Classifier: Naive Bayes classifier[1], TAN, BAN and GBN.
useful link:Decision Theory, Bayes Classifier

Bayes VS Frequentist

During the history of statistics, there are two major classification methods : Bayes and frequentist. The two methods represent two different ways of thoughts and hold different view to define probability. The followings are the main differences between Bayes and Frequentist.

Frequentist

1. Probability is objective.
2. Data is a repeatable random sample(there is a frequency).
3. Parameters are fixed and unknown constant.
4. Not applicable to single event. For example, a frequentist cannot predict the weather of tomorrow because tomorrow is only one unique event, and cannot be referred to a frequency in a lot of samples.

Bayes

1. Probability is subjective.
2. Data are fixed.
3. Parameters are unknown and random variables that have a given distribution and other probability statements can be made about them.
4. Can be applied to single events based on degree of confidence or beliefs. For example, Bayesian can predict tomorrow's weather, such as having the probability of [math]\displaystyle{ \,50% }[/math] of rain.

Example

Suppose there is a man named Jack. In bayes method, at first, one can see this man (object), and then judge whether his name is Jack (label). On the other hand, in Frequentist method, one doesn’t see the man (object), but can see the photos (label) of this man to judge whether he is Jack.

Linear and Quadratic Discriminant Analysis - October 2,2009

LDA

A Bayes classifier would be optimal. Unfortunately, the prior and conditional density of most data is not known. So some estimation of these should be made, if we want to classify some data. The simplest way to achieve this is to assume that all the class densities are approximately a multivariate normal distribution, find the parameters of each such distribution, and use them to calculate the conditional density and prior for unknown points, and thus approximate the Bayesian classifier to choose the most likely class. In addition, if the covariance of each class density is assumed to be the same, the number of unknown parameters is reduced - and the model is easy to fit and use, as seen later. The name Linear Discriminant Analysis comes from the fact that these simplications produce a linear model, which is used to discriminate between classes. In many cases, this simple model is sufficient to provide a near optimal classification - for example, the Z-Score credit risk model, designed by Edward Altman in 1968, which is essentially a weighted LDA, revisited in 2000, has shown an 85-90% success rate predicting bankruptcy, and is still in use today.

To perform LDA we make two assumptions. 1. The clusters belonging to all classes each follow a multivariate normal distribution. [math]\displaystyle{ x \in \mathbb{R}^d }[/math] [math]\displaystyle{ f_k(x)=\frac{1}{ (2\pi)^{d/2}|\Sigma_k|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k] \right) }[/math]

2. Each cluster has the same variance [math]\displaystyle{ \,\Sigma }[/math] equal to the mean variance of [math]\displaystyle{ \Sigma_k \forall k }[/math].

We wish to solve for the boundary where the error rates for classifying a point are equal, where one side of the boundary gives a lower error rate for one class and the other side gives a lower error rate for the other class.

So we solve [math]\displaystyle{ \,r_k(x)=r_l(x) }[/math] for all the pairwise combinations of classes.

[math]\displaystyle{ \,\Rightarrow Pr(Y=k|X=x)=Pr(Y=l|X=x) }[/math]

[math]\displaystyle{ \,\Rightarrow \frac{Pr(X=x|Y=k)Pr(Y=k)}{Pr(X=x)}=\frac{Pr(X=x|Y=l)Pr(Y=l)}{Pr(X=x)} }[/math] using Bayes' Theorem

[math]\displaystyle{ \,\Rightarrow Pr(X=x|Y=k)Pr(Y=k)=Pr(X=x|Y=l)Pr(Y=l) }[/math] by canceling denominators

[math]\displaystyle{ \,\Rightarrow f_k(x)\pi_k=f_l(x)\pi_l }[/math]

[math]\displaystyle{ \,\Rightarrow \frac{1}{ (2\pi)^{d/2}|\Sigma|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma^{-1} [x - \mu_k] \right)\pi_k=\frac{1}{ (2\pi)^{d/2}|\Sigma|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma^{-1} [x - \mu_l] \right)\pi_l }[/math]

[math]\displaystyle{ \,\Rightarrow \exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma^{-1} [x - \mu_k] \right)\pi_k=\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma^{-1} [x - \mu_l] \right)\pi_l }[/math] Since both [math]\displaystyle{ \Sigma }[/math] are equal based on the assumptions specific to LDA.

[math]\displaystyle{ \,\Rightarrow -\frac{1}{2} [x - \mu_k]^\top \Sigma^{-1} [x - \mu_k] + \log(\pi_k)=-\frac{1}{2} [x - \mu_l]^\top \Sigma^{-1} [x - \mu_l] +\log(\pi_l) }[/math] taking the log of both sides.

[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\left( x^\top\Sigma^{-1}x + \mu_k^\top\Sigma^{-1}\mu_k - 2x^\top\Sigma^{-1}\mu_k - x^\top\Sigma^{-1}x - \mu_l^\top\Sigma^{-1}\mu_l + 2x^\top\Sigma^{-1}\mu_l \right)=0 }[/math] by expanding out

[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\left( \mu_k^\top\Sigma^{-1}\mu_k-\mu_l^\top\Sigma^{-1}\mu_l - 2x^\top\Sigma^{-1}(\mu_k-\mu_l) \right)=0 }[/math] after canceling out like terms and factoring.

We can see that this is a linear function in x with general form ax+b=0.

Actually, this linear log function shows that the decision boundary between class [math]\displaystyle{ k }[/math] and class [math]\displaystyle{ l }[/math], i.e. [math]\displaystyle{ Pr(G=k|X=x)=Pr(G=l|X=x) }[/math], is linear in [math]\displaystyle{ x }[/math]. Given any pair of classes, decision boundaries are always linear. In [math]\displaystyle{ p }[/math] dimensions, we separate regions by hyperplanes.

In the special case where the number of samples from each class are equal ([math]\displaystyle{ \,\pi_k=\pi_l }[/math]), the boundary surface or line lies halfway between [math]\displaystyle{ \,\mu_l }[/math] and [math]\displaystyle{ \,\mu_k }[/math]

QDA

The concept is the same idea of finding a boundary where the error rate for classification between classes are equal, except the assumption that each cluster has the same variance is removed.

Following along from where QDA diverges from LDA.

[math]\displaystyle{ \,f_k(x)\pi_k=f_l(x)\pi_l }[/math]

[math]\displaystyle{ \,\Rightarrow \frac{1}{ (2\pi)^{d/2}|\Sigma_k|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k] \right)\pi_k=\frac{1}{ (2\pi)^{d/2}|\Sigma_l|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma_l^{-1} [x - \mu_l] \right)\pi_l }[/math]

[math]\displaystyle{ \,\Rightarrow \frac{1}{|\Sigma_k|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k] \right)\pi_k=\frac{1}{|\Sigma_l|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma_l^{-1} [x - \mu_l] \right)\pi_l }[/math] by cancellation

[math]\displaystyle{ \,\Rightarrow -\frac{1}{2}\log(|\Sigma_k|)-\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k]+\log(\pi_k)=-\frac{1}{2}\log(|\Sigma_l|)-\frac{1}{2} [x - \mu_l]^\top \Sigma_l^{-1} [x - \mu_l]+\log(\pi_l) }[/math] by taking the log of both sides

[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\log(\frac{|\Sigma_k|}{|\Sigma_l|})-\frac{1}{2}\left( x^\top\Sigma_k^{-1}x + \mu_k^\top\Sigma_k^{-1}\mu_k - 2x^\top\Sigma_k^{-1}\mu_k - x^\top\Sigma_l^{-1}x - \mu_l^\top\Sigma_l^{-1}\mu_l + 2x^\top\Sigma_l^{-1}\mu_l \right)=0 }[/math] by expanding out

[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\log(\frac{|\Sigma_k|}{|\Sigma_l|})-\frac{1}{2}\left( x^\top(\Sigma_k^{-1}-\Sigma_l^{-1})x + \mu_k^\top\Sigma_k^{-1}\mu_k - \mu_l^\top\Sigma_l^{-1}\mu_l - 2x^\top(\Sigma_k^{-1}\mu_k-\Sigma_l^{-1}\mu_l) \right)=0 }[/math] this time there are no cancellations, so we can only factor

The final result is a quadratic equation specifying a curved boundary between classes with general form ax²+bx+c=0.

Linear and Quadratic Discriminant Analysis cont'd - October 5, 2009

Summarizing LDA and QDA

We can summarize what we have learned on LDA and QDA so far into the following theorem.

Theorem:

Suppose that [math]\displaystyle{ \,Y \in \{1,\dots,k\} }[/math], if [math]\displaystyle{ \,f_k(x) = Pr(X=x|Y=y) }[/math] is Gaussian, the Bayes Classifier rule is:

[math]\displaystyle{ \,h(X) = \arg\max_{k} \delta_k(x) }[/math]

where

[math]\displaystyle{ \,\delta_k = - \frac{1}{2}log(|\Sigma_k|) - \frac{1}{2}(x-\mu_k)^\top\Sigma_k^{-1}(x-\mu_k) + log (\pi_k) }[/math] (quadratic)

• Note The decision boundary between classes [math]\displaystyle{ k }[/math] and [math]\displaystyle{ l }[/math] is quadratic in [math]\displaystyle{ x }[/math].

If the covariance of the Gaussians are the same, this becomes:

[math]\displaystyle{ \,\delta_k = x^\top\Sigma^{-1}\mu_k - \frac{1}{2}\mu_k^\top\Sigma^{-1}\mu_k + log (\pi_k) }[/math] (linear)

• Note [math]\displaystyle{ \,\arg\max_{k} \delta_k(x) }[/math]returns the set of k for which [math]\displaystyle{ \,\delta_k(x) }[/math] attains its largest value.

In practice

We need to estimate the prior, so in order to do this, we use the sample estimates of [math]\displaystyle{ \,\pi,\mu_k,\Sigma_k }[/math] in place of the true values, i.e.

File:estimation.png

Estimation of the probability of belonging to either class k or l

[math]\displaystyle{ \,\hat{\pi_k} = \hat{Pr}(y=k) = \frac{n_k}{n} }[/math]

[math]\displaystyle{ \,\hat{\mu_k} = \frac{1}{n_k}\sum_{i:y_i=k}x_i }[/math]

[math]\displaystyle{ \,\hat{\Sigma_k} = \frac{1}{n_k}\sum_{i:y_i=k}(x_i-\hat{\mu_k})(x_i-\hat{\mu_k})^\top }[/math]

In the case where we have a common covariance matrix, we get the ML estimate to be

[math]\displaystyle{ \,\Sigma=\frac{\sum_{r=1}^{k}(n_r\Sigma_r)}{\sum_{l=1}^{k}(n_l)} }[/math]

Computation

Case 1: (Example) [math]\displaystyle{ \, \Sigma_k = I }[/math]

This means that the data is distributed symmetrically around the center [math]\displaystyle{ \mu }[/math], i.e. the isocontours are all circles.

We have:

[math]\displaystyle{ \,\delta_k = - \frac{1}{2}log(|I|) - \frac{1}{2}(x-\mu_k)^\top I(x-\mu_k) + log (\pi_k) }[/math]

We see that the first term in the above equation, [math]\displaystyle{ \,\frac{1}{2}log(|I|) }[/math], is zero. The second term contains [math]\displaystyle{ \, (x-\mu_k)^\top I(x-\mu_k) = (x-\mu_k)^\top(x-\mu_k) }[/math], which is the squared Euclidean distance between [math]\displaystyle{ \,x }[/math] and [math]\displaystyle{ \,\mu_k }[/math]. Therefore we can find the distance between a point and each center and adjust it with the log of the prior, [math]\displaystyle{ \,log(\pi_k) }[/math]. The class that has the minimum distance will maximise [math]\displaystyle{ \,\delta_k }[/math]. According to the theorem, we can then classify the point to a specific class [math]\displaystyle{ \,k }[/math]. In addition, [math]\displaystyle{ \, \Sigma_k = I }[/math] implies that our data is spherical.

Case 2: (General Case) [math]\displaystyle{ \, \Sigma_k \ne I }[/math]

We can decompose this as:

[math]\displaystyle{ \, \Sigma_k = USV^\top = USU^\top }[/math] (since if [math]\displaystyle{ \, U = XX^\top }[/math] and [math]\displaystyle{ \, V=X^\top X }[/math] , if [math]\displaystyle{ \, X }[/math] is symmetric, [math]\displaystyle{ \, U=V }[/math] , and here [math]\displaystyle{ \, \Sigma }[/math] is symmetric)

and the inverse of [math]\displaystyle{ \,\Sigma_k }[/math] is

[math]\displaystyle{ \, \Sigma_k^{-1} = (USU^\top)^{-1} = (U^\top)^{-1}S^{-1}U^{-1} = US^{-1}U^\top }[/math] (since [math]\displaystyle{ \,U }[/math] is orthonormal)

So from the formula for [math]\displaystyle{ \,\delta_k }[/math], the second term is

[math]\displaystyle{ \, (x-\mu_k)^\top\Sigma_k^{-1}(x-\mu_k) }[/math]

[math]\displaystyle{ \, = (x-\mu_k)^\top US^{-1}U^T(x-\mu_k) }[/math]

[math]\displaystyle{ \, = (U^\top x-U^\top\mu_k)^\top S^{-1}(U^\top x-U^\top \mu_k) }[/math]

[math]\displaystyle{ \, = (U^\top x-U^\top\mu_k)^\top S^{-\frac{1}{2}}S^{-\frac{1}{2}}(U^\top x-U^\top\mu_k) }[/math]

[math]\displaystyle{ \, = (S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top\mu_k)^\top I(S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top \mu_k) }[/math]

[math]\displaystyle{ \, = (S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top\mu_k)^\top(S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top \mu_k) }[/math]

where we have the Euclidean distance between [math]\displaystyle{ \, S^{-\frac{1}{2}}U^\top x }[/math] and [math]\displaystyle{ \, S^{-\frac{1}{2}}U^\top\mu_k }[/math].

A transformation of all the data points can be done from [math]\displaystyle{ \,x }[/math] to [math]\displaystyle{ \,x^* }[/math] where [math]\displaystyle{ \, x^* \leftarrow S^{-\frac{1}{2}}U^\top x }[/math].

It is now possible to do classification with [math]\displaystyle{ \,x^* }[/math], treating it as in Case 1 above.

Note that when we have multiple classes, they must all have the same transformation, else, ahead of time we would have to assume a data point belongs to one class or the other. All classes therefore need to have the same shape for classification to be applicable using this method. So this method works for LDA.

If the classes have different shapes, in another word, have different covariance [math]\displaystyle{ \,\Sigma_k }[/math], can we use the same method to transform all data points [math]\displaystyle{ \,x }[/math] to [math]\displaystyle{ \,x^* }[/math]?

The answer is NO. Consider that you have two classes with different shapes, then consider transforming them to the same shape. Given a data point, justify which class this point belongs to. The question is, which transformation can you use? For example, if you use the transformation of class A, then you have assumed that this data point belongs to class A.

The Number of Parameters in LDA and QDA

LDA: since we just need to compare the differences between one given class and remaining [math]\displaystyle{ K-1 }[/math] classes, totally, there are [math]\displaystyle{ K-1 }[/math] differences. For each of them, [math]\displaystyle{ a^{T}x+b }[/math] requires [math]\displaystyle{ d+1 }[/math] parameters. Therefore, there are [math]\displaystyle{ (K-1)\times(d+1) }[/math] parameters.

QDA: For each of differences, [math]\displaystyle{ x^{T}ax + b^{T}x + c }[/math] requires [math]\displaystyle{ \frac{1}{2}(d+1)\times d + d + 1 = \frac{d(d+3)}{2}+1 }[/math] parameters. Therefore, there are [math]\displaystyle{ (K-1)(\frac{d(d+3)}{2}+1) }[/math] parameters.

LDA and QDA in Matlab - October 7, 2009

We have examined the theory behind Linear Discriminant Analysis (LDA) and Quadratic Discriminant Analysis (QDA) above; how do we use these algorithms in practice? Matlab offers us a function called classify that allows us to perform LDA and QDA quickly and easily.

In class, we were shown an example of using LDA and QDA on the 2_3 data that is used in the first assignment. The code below reproduces that example, slightly modified, and explains each step.

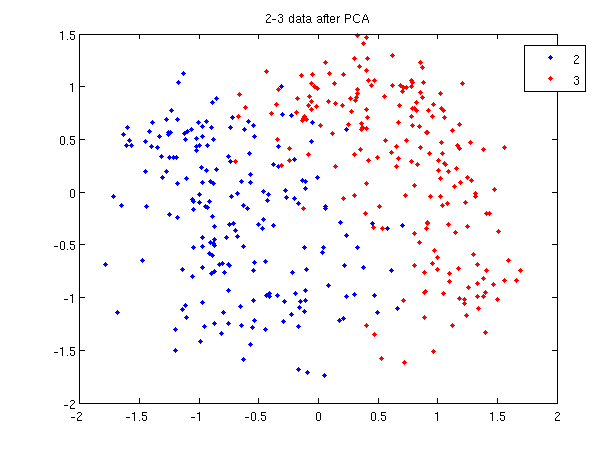
>> load 2_3;
>> [U, sample] = princomp(X');
>> sample = sample(:,1:2);

First, we do principal component analysis (PCA) on the 2_3 data to reduce the dimensionality of the original data from 64 dimensions to 2. Doing this makes it much easier to visualize the results of the LDA and QDA algorithms.

>> plot (sample(1:200,1), sample(1:200,2), '.');
>> hold on;
>> plot (sample(201:400,1), sample(201:400,2), 'r.');

Recall that in the 2_3 data, the first 200 elements are images of the number two handwritten and the last 200 elements are images of the number three handwritten. This code sets up a plot of the data such that the points that represent a 2 are blue, while the points that represent a 3 are red.

See title and legend for information on adding the title and legend.

Before using classify we can set up a vector that contains the actual labels for our data, to train the classification algorithm. If we don't know the labels for the data, then the element in the group vector should be an empty string or NaN. (See grouping data for more information.)

>> group = ones(400,1);
>> group(201:400) = 2;

We can now classify our data.

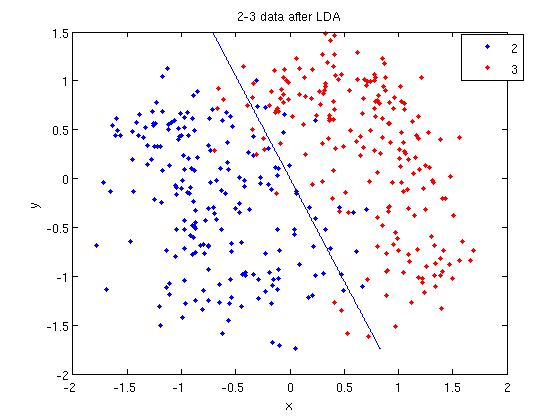
>> [class, error, POSTERIOR, logp, coeff] = classify(sample, sample, group, 'linear');

The full details of this line can be examined in the Matlab help file linked above. What we care about are class, which contains the labels that the algorithm thinks that each data point belongs to, and coeff, which contains information about the line that algorithm created to separate the data into each class.

We can see the efficacy of the algorithm by comparing class to group.

>> sum (class==group)
ans =
   369

This compares the value in class to the value in group. The answer of 369 tells us that the algorithm correctly determined the class of the point 369 times, out of a possible 400 data points. This gives us an empirical error rate of 0.0775.

We can see the line produced by LDA using coeff.

>> k = coeff(1,2).const;
>> l = coeff(1,2).linear;
>> f = sprintf('0 = %g+%g*x+%g*y', k, l(1), l(2));
>> ezplot(f, [min(sample(:,1)), max(sample(:,1)), min(sample(:,2)), max(sample(:,2))]);

Those familiar with the programming language C will find the sprintf line refreshingly familiar; those with no exposure to C are directed to Matlab's sprintf page. Essentially, this code sets up the equation of the line in the form 0 = a + bx + cy. We then use the ezplot function to plot the line.

The 2-3 data after LDA is performed. The line shows where the two classes are split.

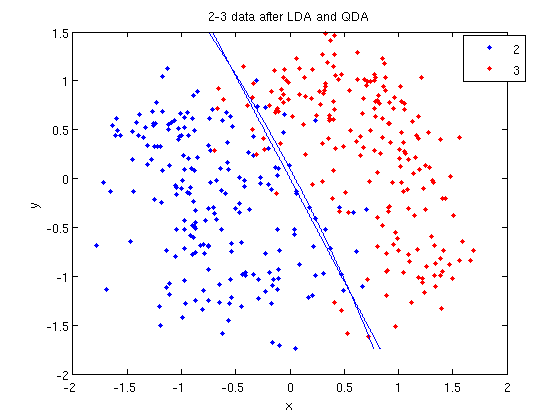
Let's perform the same steps, except this time using QDA. The main difference with QDA is a slightly different call to classify, and a more complicated procedure to plot the line.

>> [class, error, POSTERIOR, logp, coeff] = classify(sample, sample, group, 'quadratic');
>> sum (class==group)
ans =
   371
>> k = coeff(1,2).const;
>> l = coeff(1,2).linear;
>> q = coeff(1,2).quadratic;
>> f = sprintf('0 = %g+%g*x+%g*y+%g*x^2+%g*x.*y+%g*y.^2', k, l, q(1,1), q(1,2)+q(2,1), q(2,2));
>> ezplot(f, [min(sample(:,1)), max(sample(:,1)), min(sample(:,2)), max(sample(:,2))]);

The 2-3 data after QDA is performed. The curved line shows where QDA splits the two classes. Note that it is only correct 2 in 2 more data points compared to LDA; we can see a blue point and a red point that lie on the correct side of the curve that do not lie on the correct side of the line.

classify can also be used with other discriminant analysis algorithms. The steps laid out above would only need to be modified slightly for those algorithms.

Trick: Using LDA to do QDA - October 7, 2009

There is a trick that allows us to use the linear discriminant analysis (LDA) algorithm to generate as its output a quadratic function that can be used to classify data. This trick is similar to, but more primitive than, the Kernel trick that will be discussed later in the course.

Essentially, the trick involves adding one or more new features (i.e. new dimensions) that just contain our original data projected to that dimension. We then do LDA on our new higher-dimensional data. The answer provided by LDA can then be collapsed onto a lower dimension, giving us a quadratic answer.

Motivation

Why would we want to use LDA over QDA? In situations where we have fewer data points, LDA turns out to be more robust.

If we look back at the equations for LDA and QDA, we see that in LDA we must estimate [math]\displaystyle{ \mu_1 }[/math], [math]\displaystyle{ \mu_2 }[/math] and [math]\displaystyle{ \Sigma }[/math]. In QDA we must estimate all of those, plus another [math]\displaystyle{ \Sigma }[/math]; the extra [math]\displaystyle{ \frac{d(d-1)}{2} }[/math] estimations make QDA less robust with fewer data points.

Theoretically

Suppose we can estimate some vector [math]\displaystyle{ \underline{w}^T }[/math] such that

[math]\displaystyle{ y = \underline{w}^Tx }[/math]

where [math]\displaystyle{ \underline{w} }[/math] is a d-dimensional column vector, and [math]\displaystyle{ x\ \epsilon\ \Re^d }[/math] (vector in d dimensions).

We also have a non-linear function [math]\displaystyle{ g(x) = y = x^Tvx + \underline{w}^Tx }[/math] that we cannot estimate.

Using our trick, we create two new vectors, [math]\displaystyle{ \underline{w}^* }[/math] and [math]\displaystyle{ x^* }[/math] such that:

[math]\displaystyle{ \underline{w}^{*T} = [w_1,w_2,...,w_d,v_1,v_2,...,v_d] }[/math]

and

[math]\displaystyle{ x^{*T} = [x_1,x_2,...,x_d,{x_1}^2,{x_2}^2,...,{x_d}^2] }[/math]

We can then estimate a new function, [math]\displaystyle{ g^*(x,x^2) = y^* = \underline{w}^{*T}x^* }[/math].

Note that we can do this for any [math]\displaystyle{ x }[/math] and in any dimension; we could extend a [math]\displaystyle{ D \times n }[/math] matrix to a quadratic dimension by appending another [math]\displaystyle{ D \times n }[/math] matrix with the original matrix squared, to a cubic dimension with the original matrix cubed, or even with a different function altogether, such as a [math]\displaystyle{ sin(x) }[/math] dimension.

By Example

Let's use our trick to do a quadratic analysis of the 2_3 data using LDA.

>> load 2_3;
>> [U, sample] = princomp(X');
>> sample = sample(:,1:2);

We start off the same way, by using PCA to reduce the dimensionality of our data to 2.

>> X_star = zeros(400,4);
>> X_star(:,1:2) = sample(:,:);
>> for i=1:400
     for j=1:2
       X_star(i,j+2) = X_star(i,j)^2;
     end
   end

This projects our sample into two more dimensions by squaring our initial two dimensional data set.

>> group = ones(400,1);
>> group(201:400) = 2;
>> [class, error, POSTERIOR, logp, coeff] = classify(X_star, X_star, group, 'linear');
>> sum (class==group)
ans =
   375

We can now display our results.

>> k = coeff(1,2).const;
>> l = coeff(1,2).linear;
>> f = sprintf('0 = %g+%g*x+%g*y+%g*(x)^2+%g*(y)^2', k, l(1), l(2),l(3),l(4));
>> ezplot(f,[min(sample(:,1)), max(sample(:,1)), min(sample(:,2)), max(sample(:,2))]);

The plot shows the quadratic decision boundary obtained using LDA in the four-dimensional space on the 2_3.mat data. Counting the blue and red points that are on the wrong side of the decision boundary, we can confirm that we have correctly classified 375 data points.

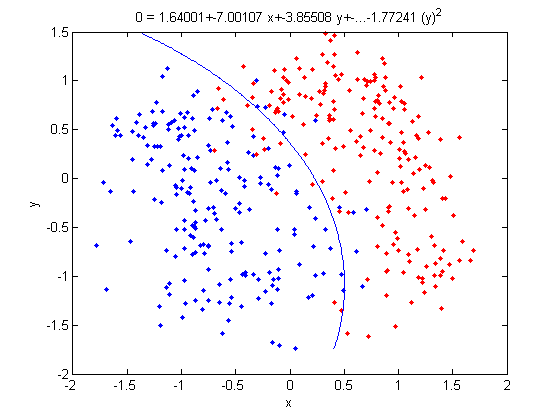
Not only does LDA give us a better result than it did previously, it actually beats QDA, which only correctly classified 371 data points for this data set. Continuing this procedure by adding another two dimensions with [math]\displaystyle{ x^4 }[/math] (i.e. we set X_star(i,j+2) = X_star(i,j)^4) we can correctly classify 376 points.

Introduction to Fisher's Discriminant Analysis - October 7, 2009

Fisher's Discriminant Analysis (FDA), also known as Fisher's Linear Discriminant Analysis (LDA) in some sources, is a classical feature extraction technique. It was originally described in 1936 by Sir Ronald Aylmer Fisher, an English statistician and eugenicist (!) who has been described as one of the founders of modern statistical science. His original paper describing FDA can be found here; a Wikipedia article summarizing the algorithm can be found here.

The goal of FDA starkly contrasts with our other main feature extraction technique, principal component analysis (PCA).

• In PCA, we map data to lower dimensions to maximize the variation in those dimensions.
• In FDA, we map data to lower dimensions to best separate data in different classes.

2 clouds of data, and the lines that might be produced by PCA and FDA.

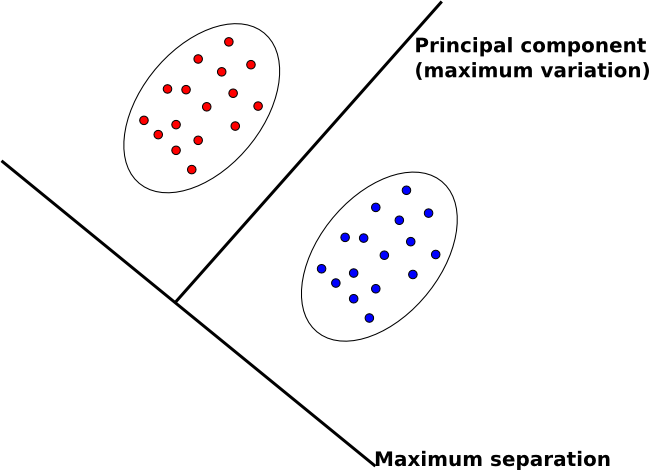
Because we are concerned with identifying which class data belongs to, FDA should be a better feature extraction algorithm for classification.

Another difference between PCA and FDA is that FDA is a supervised algorithm; that is, we know what class data belongs to, and we exploit that knowledge to find a good projection to lower dimensions.

An intuitive description of FDA can be given by visualizing two clouds of data, as shown above. Ideally, we would like to collapse all of the data points in each cloud onto one point on some projected line, then make those two points as far apart as possible. In doing so, we make it very easy to tell which class a data point belongs to. In practice, it is not possible to collapse all of the points in a cloud to one point, but we attempt to make all of the points in a cloud close to each other while simultaneously far from the points in the other cloud.

Example in R

PCA and FDA primary dimension for normal multivariate data, using R.

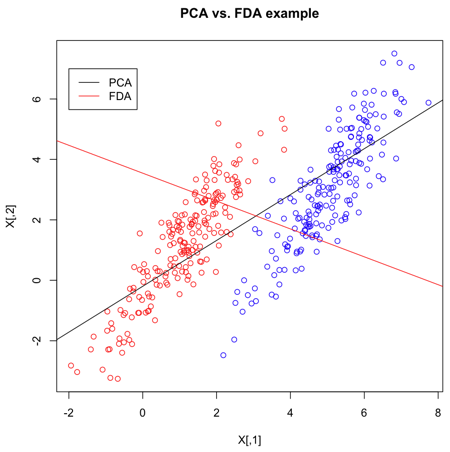
>> X = matrix(nrow=400,ncol=2)
>> X[1:200,] = mvrnorm(n=200,mu=c(1,1),Sigma=matrix(c(1,1.5,1.5,3),2))
>> X[201:400,] = mvrnorm(n=200,mu=c(5,3),Sigma=matrix(c(1,1.5,1.5,3),2))
>> Y = c(rep("red",200),rep("blue",200))

Create 2 multivariate normal random variables with [math]\displaystyle{ \, \mu_1 = \left( \begin{array}{c}1 \\ 1 \end{array} \right), \mu_2 = \left( \begin{array}{c}5 \\ 3 \end{array} \right). ~\textrm{Cov} = \left( \begin{array}{cc} 1 & 1.5 \\ 1.5 & 3 \end{array} \right) }[/math]. Create Y, an index indicating which class they belong to.

>> s <- svd(X,nu=1,nv=1)

Calculate the SVD decomposition of X. The most significant direction is in s$v[,1], and is displayed as a black line.

>> s2 <- lda(X,grouping=Y)

The lda function, given the group for each item, uses FLDA to find the most discriminant direction. This can be found in s2$scaling.

>> plot(X,col=Y,main="PCA vs. FDA example")
>> slope = s$v[2]/s$v[1]
>> intercept = mean(X[,2])-slope*mean(X[,1])
>> abline(a=intercept,b=slope)
>> slope2 = s2$scaling[2]/s2$scaling[1]
>> intercept2 = mean(X[,2])-slope2*mean(X[,1])
>> abline(a=intercept2,b=slope2,col="red")
>> legend(-2,7,legend=c("PCA","FDA"),col=c("black","red"),lty=1)

Code to reproduce the picture given above.

Ficher's Discriminant Analysis (FDA) - October 9, 2009

With FDA, the idea is to reduce the dimensionality of data in order to have separable data points in a new space. We can consider two kinds of problems:

• 2-class problem
• multi-class problem

Two-class problem

In the two-class problem,

[math]\displaystyle{ \underline{\mu_{1}}=\frac{1}{n_{1}}\displaystyle\sum_{i:y_{i}=1}\underline{x_{i}}, \quad\displaystyle\Sigma_{1},\quad\underline{\mu_{2}}=\frac{1}{n_{2}}\displaystyle\sum_{i:y_{i}=2}\underline{x_{i}},\ and\quad\displaystyle\Sigma_{2}\quad }[/math] represent the mean and covariance of class 1 and 2 respectively. Essentially, there are two goals:

1.To make the means of these two classes as far apart as possible

In other words, the goal is to maximize the distance after projection between class 1 and class 2. This can be done by maximizing the distance between the means of the classes after projection. When projecting the data points to a one-dimensional space, all points will be projected to a single line; this is the line with the direction that achieves maximum separation of classes upon projetion. If the original points are [math]\displaystyle{ \underline{x_{i}} \in \mathbb{R}^{d} }[/math]and the projected points are [math]\displaystyle{ \underline{w}^T \underline{x_{i}} }[/math] then the mean of the projected points will be [math]\displaystyle{ \underline{w}^T \underline{\mu_{1}} }[/math] and [math]\displaystyle{ \underline{w}^T \underline{\mu_{2}} }[/math] for class 1 and class 2 respectively. The goal now becomes to maximize the Euclidean distance between projected means, [math]\displaystyle{ (\underline{w}^T\underline{\mu_{1}}-\underline{w}^T\underline{\mu_{2}})^T (\underline{w}^T\underline{\mu_{1}}-\underline{w}^T\underline{\mu_{2}}) }[/math]. The steps of this maximization are given below.

2.We want to collapse all data points of each class to a single point, ie., minimize the covariance within classes

Notice that the variance of the projected classes 1 and 2 are given by [math]\displaystyle{ \underline{w}^T\Sigma_{1}\underline{w} }[/math] and [math]\displaystyle{ \underline{w}^T\Sigma_{2}\underline{w} }[/math]. The second goal is to minimize the sum of these two covariances. As is demonstrated below, both of these goals can be accomplished simultaneously.

Original points are [math]\displaystyle{ \underline{x_{i}} \in \mathbb{R}^{d} }[/math]
Projected points are [math]\displaystyle{ \underline{z_{i}} \in \mathbb{R}^{1} }[/math] with [math]\displaystyle{ \underline{z_{i}} = \underline{w}^T .\underline{x_{i}} }[/math]

Between class covariance

In this particular case, we want to project all the data points in one dimensional space.

[math]\displaystyle{ \,(\underline{w}^T \underline{\mu_{1}} - \underline{w}^T \underline{\mu_{2}})^T(\underline{w}^T \underline{\mu_{1}} - \underline{w}^T \underline{\mu_{2}}) }[/math]

[math]\displaystyle{ \,= (\underline{\mu_{1}}-\underline{\mu_{2}})^T\underline{w} . \underline{w}^T(\underline{\mu_{1}}-\underline{\mu_{2}}) }[/math]

[math]\displaystyle{ \,= \underline{w}^T(\underline{\mu_{1}}-\underline{\mu_{2}})(\underline{\mu_{1}}-\underline{\mu_{2}})^T\underline{w} . }[/math]

The quantity [math]\displaystyle{ (\underline{\mu_{1}}-\underline{\mu_{2}})(\underline{\mu_{1}}-\underline{\mu_{2}})^T }[/math] is called between class covariance or [math]\displaystyle{ S_{B} }[/math].

The goal is to maximize : [math]\displaystyle{ \underline{w}^T S_{B} \underline{w} }[/math]

Within class covariance

Covariance of class 1 is [math]\displaystyle{ \Sigma_{1} }[/math] Covariance of class 2 is [math]\displaystyle{ \Sigma_{2} }[/math] So covariance of projected points will be [math]\displaystyle{ \underline{w}^T \Sigma_{1} \underline{w} }[/math] and [math]\displaystyle{ \underline{w}^T \Sigma_{2} \underline{w} }[/math]

If we sum this two quantities we have:

[math]\displaystyle{ \,\underline{w}^T \Sigma_{1} \underline{w} + \underline{w}^T \Sigma_{2} \underline{w} }[/math]

[math]\displaystyle{ \,= \underline{w}^T(\Sigma_{1} + \Sigma_{2})\underline{w} }[/math]

The quantity [math]\displaystyle{ (\Sigma_{1} + \Sigma_{2}) }[/math] is called within class covariance or [math]\displaystyle{ S_{W} }[/math]

The goal is to minimize : [math]\displaystyle{ \underline{w}^T S_{W} \underline{w} }[/math]

Objective Function

Insteat of maximizing [math]\displaystyle{ \underline{w}^T S_{B} \underline{w} }[/math] and minimizing [math]\displaystyle{ \underline{w}^T S_{W} \underline{w} }[/math] we can define the following objective function:

[math]\displaystyle{ \underset{\underline{w}}{max}\ \frac{\underline{w}^T S_{B} \underline{w}}{\underline{w}^T S_{W} \underline{w}} }[/math] It's equivalent to [math]\displaystyle{ \underset{\underline{w}}{max}\ \underline{w}^T S_{B} \underline{w} }[/math] subject to constraint [math]\displaystyle{ \underline{w}^T S_{W} \underline{w}\ =\ 1 }[/math]

[math]\displaystyle{ L(\underline{w},\lambda) = \underline{w}^T S_{B} \underline{w} - \lambda(\underline{w}^T S_{W} \underline{w} - 1) }[/math]

With [math]\displaystyle{ \frac{\part L}{\part \underline{w}} = 0 }[/math]

[math]\displaystyle{ \Rightarrow\ 2\ S_{B}\ \underline{w}\ - 2\lambda\ S_{W}\ \underline{w}\ = 0 }[/math]

[math]\displaystyle{ \Rightarrow\ S_{B}\ \underline{w}\ =\ \lambda\ S_{W}\ \underline{w} }[/math]

[math]\displaystyle{ \Rightarrow\ S_{w}^{-1}\ S_{B}\ \underline{w}\ =\ \lambda\ \underline{w} }[/math]

Here [math]\displaystyle{ \underline{w} }[/math] is the eigenvector of [math]\displaystyle{ S_{w}^{-1}\ S_{B} }[/math] corresponding to the largest eigenvalue.

In facts, this expression can be simplified even more.

[math]\displaystyle{ \Rightarrow\ S_{w}^{-1}\ S_{B}\ \underline{w}\ =\ \lambda\ \underline{w} }[/math] with [math]\displaystyle{ S_{B}\ =\ (\underline{\mu_{1}}-\underline{\mu_{2}})(\underline{\mu_{1}}-\underline{\mu_{2}})^T }[/math]

[math]\displaystyle{ \Rightarrow\ S_{w}^{-1}\ (\underline{\mu_{1}}-\underline{\mu_{2}})(\underline{\mu_{1}}-\underline{\mu_{2}})^T \underline{w}\ =\ \lambda\ \underline{w} }[/math]

The quantity [math]\displaystyle{ (\underline{\mu_{1}}-\underline{\mu_{2}})^T \underline{w} }[/math] and [math]\displaystyle{ \lambda }[/math] are scalars.
So we can say the quantity [math]\displaystyle{ S_{w}^{-1}\ (\underline{\mu_{1}}-\underline{\mu_{2}}) }[/math] is proportional to [math]\displaystyle{ \underline{w} }[/math]