stat841

Course Note for Sept.30th (Classfication_by Liang Jiaxi)

Review of LLE

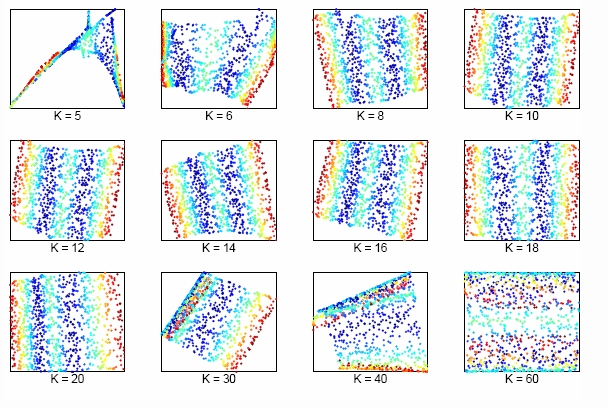
The size of neighborhood chosen in LLE influences the effect of LLE. The picture above shows the effect of neighborhood size to LLE of the two dimensional S-manifold in the top panels. We can lower dimension from D=3 to d=2 by choosing K nearest neighbors. Apparently, when K is too small or too large, the LLE fails to find out the two main degree of freedom.

Classification

In classification we attempt to approximate a function [math]\displaystyle{ h }[/math], by using a training data set, that will then be able to accurately classify new data inputs.

Given,
[math]\displaystyle{ \mathcal{X} \subset \mathbb{R}^{d} }[/math], a subset of the D-dimensional real vectors and
[math]\displaystyle{ \mathcal{Y} }[/math], a finite set of labels

We try to determine a 'classification rule' [math]\displaystyle{ h }[/math] such that,

[math]\displaystyle{ \,h: \mathcal{X} \mapsto \mathcal{Y} }[/math]

We use n ordered pairs of training data to approximate [math]\displaystyle{ h }[/math],
[math]\displaystyle{ \,\{(X_{1},Y_{1}), (X_{2},Y_{2}), \dots , (X_{n},Y_{n})\} }[/math], [math]\displaystyle{ \,X_{i} \in \mathcal{X} }[/math],[math]\displaystyle{ \,Y_{i} \in \mathcal{Y} }[/math].

Thus, given a new input,
[math]\displaystyle{ \,X \in \mathcal{X} }[/math]
by using the classification rule we can predict a corresponding [math]\displaystyle{ \,\hat{Y}=h(X) }[/math]

Example Suppose we wish to classify fruit into apples and oranges by considering certain features of the fruit. Let [math]\displaystyle{ \mathcal{X}_{i} }[/math]= (colour, diameter, weight) for fruit i and [math]\displaystyle{ \mathcal{Y} }[/math]={apple, orange}. The goal is to find a classification rule such that when a new fruit [math]\displaystyle{ \mathcal{X} }[/math] is presented, it can be classified as either an apple or an orange.

Error data

'True error rate' of a classifier(h) is defined as the probability that [math]\displaystyle{ \hat{Y} }[/math] predicted from [math]\displaystyle{ \,X }[/math] by classifier [math]\displaystyle{ \,h }[/math] does not actually equal to [math]\displaystyle{ \,Y }[/math], namely, [math]\displaystyle{ \, L(h)=P(h(X) \neq Y) }[/math].

'Empirical error rate(training error rate)' of a classifier(h) is defined as the frequency that [math]\displaystyle{ \hat{Y} }[/math] predicted from [math]\displaystyle{ \,X }[/math] by [math]\displaystyle{ \,h }[/math] does not equal [math]\displaystyle{ \,Y }[/math] in n predictions. The mathematical expression is:

[math]\displaystyle{ \, L_{h}= \frac{1}{n} \sum_{i=1}^{n} I(h(X_{i}) \neq Y_{i}) }[/math], where [math]\displaystyle{ \,I }[/math] is an indicator that [math]\displaystyle{ \, I= \left\{\begin{matrix} 1 & h(X_i) \neq Y_i \\ 0 & h(X_i)=Y_i \end{matrix}\right. }[/math].

Bayes Classifier

Consider the special case that [math]\displaystyle{ \,Y }[/math] has only two possible values, that is, [math]\displaystyle{ \, \mathcal{Y}=\{0, 1\} }[/math]. Consider the probability that [math]\displaystyle{ \,r(X)=P\{Y=1|X=x\} }[/math]. Given [math]\displaystyle{ \,x }[/math], if [math]\displaystyle{ \,P(Y=1|X=x)\gt P(Y=0|X=x) }[/math], then [math]\displaystyle{ \,Y }[/math] is more likely to be 1 when [math]\displaystyle{ \,X=x }[/math]. But since [math]\displaystyle{ \, 0, 1 \in \mathcal{Y} }[/math] is labels, it is meaningless to measure the conditional prabobility of [math]\displaystyle{ \,Y }[/math]. Thus, by Bayes formula, we have

[math]\displaystyle{ \,r(X)=P(Y=1|X=x)=\frac{P(X=x|Y=1)P(Y=1)}{P(X=x)}=\frac{P(X=x|Y=1)P(Y=1)}{P(X=x|Y=1)P(Y=1)+P(X=x|Y=0)P(Y=0)} }[/math]

Definition:

The Bayes classification rule [math]\displaystyle{ \,h }[/math] is:

[math]\displaystyle{ \, h(X)= \left\{\begin{matrix} 1 & r(x)\gt \frac{1}{2} \\ 0 & otherwise \end{matrix}\right. }[/math]

The set [math]\displaystyle{ \,D(h)=\{x: P(Y=1|X=x)=P(Y=0|X=x)\} }[/math] is called the decision boundary.

'Important Theorem': The Bayes rule is optimal in true error rate, that is for any other classification rule [math]\displaystyle{ \, \overline{h} }[/math], we have [math]\displaystyle{ \,L(\overline{h}) \le L(h) }[/math].

Notice: Although the Bayes rule is optimal, we still need other methods, and the reason for the fact is that in the Bayes equation discussed before, it is generally impossible for us to know the [math]\displaystyle{ \,P(Y=1) }[/math], and [math]\displaystyle{ \,P(X=x|Y=1) }[/math] and ultimately calculate the value of [math]\displaystyle{ \,r(X) }[/math], which makes Bayes rule inconvenient in practice.

Bayes VS Frequentist

During the history of statistics, there are two major classification method : Bayes and frequentist. The two methods represent two different ways of thoughts and hold different view to define probability. The following are the main differences between Bayes and Frequentist.

Frequentist

1. Probability is objective and refers to the limit of an event's relative frequency in a large number of trials.
2. Data is a repeatable random sample(there is a frequency).
3. Parameters are fixed and unknown constant.
4. Not applicable to single event. For example, a frequentist cannot predict the weather of tomorrow because tomorrow is only one unique event, and cannot be referred to a frequency in a lot of samples.

Bayes

1. Probability is subjective.
2. Data are fixed.
3. Parameters are unknown and random variables that have a given distribution and other probability statements can be made about them.
4. Can be applied to single events based on degree of confidence or beliefs. For example, Bayesian can predict tomorrow's weather as having [math]\displaystyle{ \,50% }[/math] of rain.

Example

Suppose there is a man named Jack. In bayes method, at first, one can see this man (object), and then judge whether his name is Jack (label). On the other hand, in Frequentist method, one doesn’t see the man (object), but can see the photos (label) of this man to judge whether he is Jack.

Linear and Quadratic Discriminant Analysis - October 2,2009

LDA

To perform LDA we make two assumptions. 1. The clusters belonging to all classes each follow a multivariate normal distribution. [math]\displaystyle{ x \in \mathbb{R}^d }[/math] [math]\displaystyle{ f_k(x)=\frac{1}{ (2\pi)^{d/2}|\Sigma_k|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k] \right) }[/math]

2. Each cluster has the same variance [math]\displaystyle{ \,\Sigma }[/math] equal to the mean variance of [math]\displaystyle{ \Sigma_k \forall k }[/math].

We wish to solve for the boundary where the error rates for classifying a point are equal, where one side of the boundary gives a lower error rate for one class and the other side gives a lower error rate for the other class.

So we solve [math]\displaystyle{ \,r_k(x)=r_l(x) }[/math] for all the pairwise combinations of classes.

[math]\displaystyle{ \,\Rightarrow Pr(Y=k|X=x)=Pr(Y=l|X=x) }[/math]

[math]\displaystyle{ \,\Rightarrow \frac{Pr(X=x|Y=k)Pr(Y=k)}{Pr(X=x)}=\frac{Pr(X=x|Y=l)Pr(Y=l)}{Pr(X=x)} }[/math] using Bayes' Theorem

[math]\displaystyle{ \,\Rightarrow Pr(X=x|Y=k)Pr(Y=k)=Pr(X=x|Y=l)Pr(Y=l) }[/math] by canceling denominators

[math]\displaystyle{ \,\Rightarrow f_k(x)\pi_k=f_l(x)\pi_l }[/math]

[math]\displaystyle{ \,\Rightarrow \frac{1}{ (2\pi)^{d/2}|\Sigma|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma^{-1} [x - \mu_k] \right)\pi_k=\frac{1}{ (2\pi)^{d/2}|\Sigma|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma^{-1} [x - \mu_l] \right)\pi_l }[/math]

[math]\displaystyle{ \,\Rightarrow \exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma^{-1} [x - \mu_k] \right)\pi_k=\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma^{-1} [x - \mu_l] \right)\pi_l }[/math] Since both [math]\displaystyle{ \Sigma }[/math] are equal based on the assumptions specific to LDA.

[math]\displaystyle{ \,\Rightarrow -\frac{1}{2} [x - \mu_k]^\top \Sigma^{-1} [x - \mu_k] + \log(\pi_k)=-\frac{1}{2} [x - \mu_l]^\top \Sigma^{-1} [x - \mu_l] +\log(\pi_l) }[/math] taking the log of both sides.

[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\left( x^\top\Sigma^{-1}x + \mu_k^\top\Sigma^{-1}\mu_k - 2x^\top\Sigma^{-1}\mu_k - x^\top\Sigma^{-1}x - \mu_l^\top\Sigma^{-1}\mu_l + 2x^\top\Sigma^{-1}\mu_l \right)=0 }[/math] by expanding out

[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\left( \mu_k^\top\Sigma^{-1}\mu_k-\mu_l^\top\Sigma^{-1}\mu_l - 2x^\top\Sigma^{-1}(\mu_k-\mu_l) \right)=0 }[/math] after canceling out like terms and factoring.

In the special case where the number of samples from each class are equal ([math]\displaystyle{ \pi_k=\pi_l }[/math])

The boundary surface or line lies halfway between [math]\displaystyle{ \mu_l }[/math] and [math]\displaystyle{ \mu_k }[/math]

QDA

The concept is the same idea of finding a boundary where the error rate for classification between classes are equal, except the assumption that each cluster has the same variance is removed.

Following along from where QDA diverges from LDA.

[math]\displaystyle{ \,f_k(x)\pi_k=f_l(x)\pi_l }[/math]

[math]\displaystyle{ \,\Rightarrow \frac{1}{ (2\pi)^{d/2}|\Sigma_k|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k] \right)\pi_k=\frac{1}{ (2\pi)^{d/2}|\Sigma_l|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma_l^{-1} [x - \mu_l] \right)\pi_l }[/math]

[math]\displaystyle{ \,\Rightarrow \frac{1}{|\Sigma_k|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k] \right)\pi_k=\frac{1}{|\Sigma_l|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma_l^{-1} [x - \mu_l] \right)\pi_l }[/math] by cancellation

[math]\displaystyle{ \,\Rightarrow -\frac{1}{2}\log(|\Sigma_k|)-\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k]+\log(\pi_k)=-\frac{1}{2}\log(|\Sigma_l|)-\frac{1}{2} [x - \mu_l]^\top \Sigma_l^{-1} [x - \mu_l]+\log(\pi_l) }[/math] by taking the log of both sides

[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\log(\frac{|\Sigma_k|}{|\Sigma_l|})-\frac{1}{2}\left( x^\top\Sigma_k^{-1}x + \mu_k^\top\Sigma_k^{-1}\mu_k - 2x^\top\Sigma_k^{-1}\mu_k - x^\top\Sigma_l^{-1}x - \mu_l^\top\Sigma_l^{-1}\mu_l + 2x^\top\Sigma_l^{-1}\mu_l \right)=0 }[/math] by expanding out

[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\log(\frac{|\Sigma_k|}{|\Sigma_l|})-\frac{1}{2}\left( x^\top(\Sigma_k^{-1}-\Sigma_l^{-1})x + \mu_k^\top\Sigma_k^{-1}\mu_k - \mu_l^\top\Sigma_l^{-1}\mu_l - 2x^\top(\Sigma_k^{-1}\mu_k-\Sigma_l^{-1}\mu_l) \right)=0 }[/math] this time there are no cancellations, so we can only factor

The final result is a quadratic equation specifying a curved boundary between classes.

Linear and Quadratic Discriminant Analysis cont'd - October 5, 2009

Summarizing LDA and QDA

We can summarize what we have learnt on LDA and QDA so far into the following theorem.

Theorem:

Suppose that [math]\displaystyle{ \,Y \in \{1,\dots,k\} }[/math], if [math]\displaystyle{ \,f_k(x) = Pr(X=x|Y=y) }[/math] is Gaussian, the Bayes Classifier rule is:

[math]\displaystyle{ \,h(X) = \arg\max_{k} \delta_k(x) }[/math]

where

[math]\displaystyle{ \,\delta_k = - \frac{1}{2}log(|\Sigma_k|) - \frac{1}{2}(x-\mu_k)^\top\Sigma_k^{-1}(x-\mu_k) + log (\pi_k) }[/math] (quadratic)

If the covariance of the Gaussians are the same, this becomes:

[math]\displaystyle{ \,\delta_k = x^\top\Sigma^{-1}\mu_k - \frac{1}{2}\mu_k^\top\Sigma^{-1}\mu_k + log (\pi_k) }[/math] (linear)

In practice

We need to estimate the prior, so in order to do this, we use the sample estimates of [math]\displaystyle{ \,\pi,\mu_k,\Sigma_k }[/math] in place of the true values, i.e.

File:estimation.png

Estimation of the probability of belonging to either class k or l

[math]\displaystyle{ \,\hat{\pi_k} = \hat{Pr}(y=k) = \frac{n_k}{n} }[/math]

[math]\displaystyle{ \,\hat{\mu_k} = \frac{1}{n_k}\sum_{i:y_i=k}x_i }[/math]

[math]\displaystyle{ \,\hat{\Sigma_k} = \frac{1}{n_k}\sum_{i:y_i=k}(x_i-\hat{\mu_k})(x_i-\hat{\mu_k})^\top }[/math]

In the case where we have a common covariance matrix, we get the ML estimate to be

[math]\displaystyle{ \,\Sigma=\frac{\sum_{r=1}^{k}(n_r\Sigma_r)}{\sum_{l=1}^{k}(n_l)} }[/math]

Computation

Case 1: (Example) [math]\displaystyle{ \, \Sigma_k = I }[/math]

We have:

[math]\displaystyle{ \,\delta_k = - \frac{1}{2}log(|I|) - \frac{1}{2}(x-\mu_k)^\top I(x-\mu_k) + log (\pi_k) }[/math]

We see that the first term in the above equation, [math]\displaystyle{ \,\frac{1}{2}log(|I|) }[/math], is zero. The second term contains [math]\displaystyle{ \, (x-\mu_k)^\top I(x-\mu_k) = (x-\mu_k)^\top(x-\mu_k) }[/math], which is the euclidean distance between [math]\displaystyle{ \,x }[/math] and [math]\displaystyle{ \,\mu_k }[/math]. Therefore we can find the distance between a point and each center and adjust it with the log of the prior, [math]\displaystyle{ \,log(\pi_k) }[/math]. The class that has the minimum distance will maximise [math]\displaystyle{ \,\delta_k }[/math]. According to the theorem, we can then classify the point to a specific class [math]\displaystyle{ \,k }[/math].

Case 2: (General Case) [math]\displaystyle{ \, \Sigma_k \ne I }[/math]

We can decompose this as:

[math]\displaystyle{ \, \Sigma_k = USV^\top = USU^\top }[/math] (since if [math]\displaystyle{ \, U = XX^\top }[/math] and [math]\displaystyle{ \, V=X^\top X }[/math] , if [math]\displaystyle{ \, X }[/math] is symmetric, [math]\displaystyle{ \, U=V }[/math] , and here [math]\displaystyle{ \, \Sigma }[/math] is symmetric)

and the inverse of [math]\displaystyle{ \,\Sigma_k }[/math] is

[math]\displaystyle{ \, \Sigma_k^{-1} = (USU^\top)^{-1} = (U^\top)^{-1}S^{-1}U^{-1} = US^{-1}U^\top }[/math] (since [math]\displaystyle{ \,U }[/math] is orthonormal)

So from the formula for [math]\displaystyle{ \,\delta_k }[/math], the second term is

[math]\displaystyle{ \, (x-\mu_k)^\top\Sigma_k^{-1}(x-\mu_k) }[/math]

[math]\displaystyle{ \, = (x-\mu_k)^\top US^{-1}U^T(x-\mu_k) }[/math]

[math]\displaystyle{ \, = (U^\top x-U^\top\mu_k)^\top S^{-1}(U^\top x-U^\top \mu_k) }[/math]

[math]\displaystyle{ \, = (U^\top x-U^\top\mu_k)^\top S^{-\frac{1}{2}}S^{-\frac{1}{2}}(U^\top x-U^\top\mu_k) }[/math]

[math]\displaystyle{ \, = (S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top\mu_k)^\top I(S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top \mu_k) }[/math]

[math]\displaystyle{ \, = (S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top\mu_k)^\top(S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top \mu_k) }[/math]

where we have the euclidean distance between [math]\displaystyle{ \, (S^{-\frac{1}{2}}U^\top x }[/math] and [math]\displaystyle{ \, S^{-\frac{1}{2}}U^\top\mu_k) }[/math].

A transformation of all the data points can be done from [math]\displaystyle{ \,x }[/math] to [math]\displaystyle{ \,x^* }[/math] where [math]\displaystyle{ \, x^* \leftarrow S^{-\frac{1}{2}}U^\top x }[/math].

It is now possible to do classification with [math]\displaystyle{ \,x^* }[/math], treating it as in Case 1 above.

Note that when we have multiple classes, they must all have the same transformation, else, ahead of time we would have to assume a data point belongs to one class or the other. All classes therefore need to have the same shape for classification to be applicable using this method.