XGBoost: A Scalable Tree Boosting System

Presented by

• Qianying Zhao
• Hui Huang
• Lingyun Yi
• Jiayue Zhang
• Siao Chen
• Rongrong Su
• Gezhou Zhang
• Meiyu Zhou

2 Tree Boosting In A Nutshell

2.1 Regularized Learning Objective

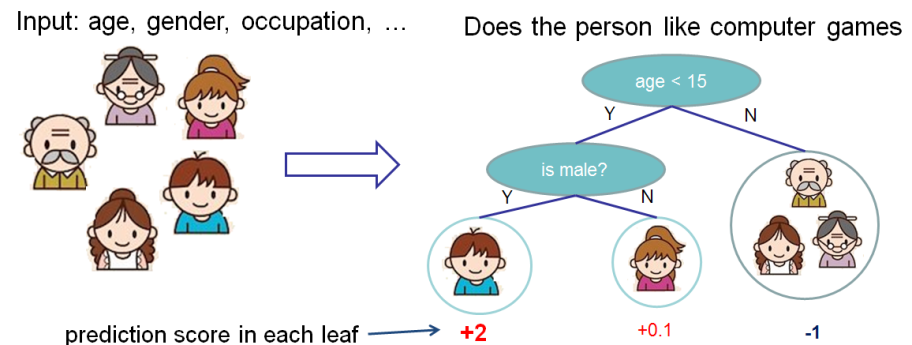
1. Regression Decision Tree (also known as classification and regression tree):

• Decision rules are the same as in decision tree
• Contains one score in each leaf value

2. Model and Parameter

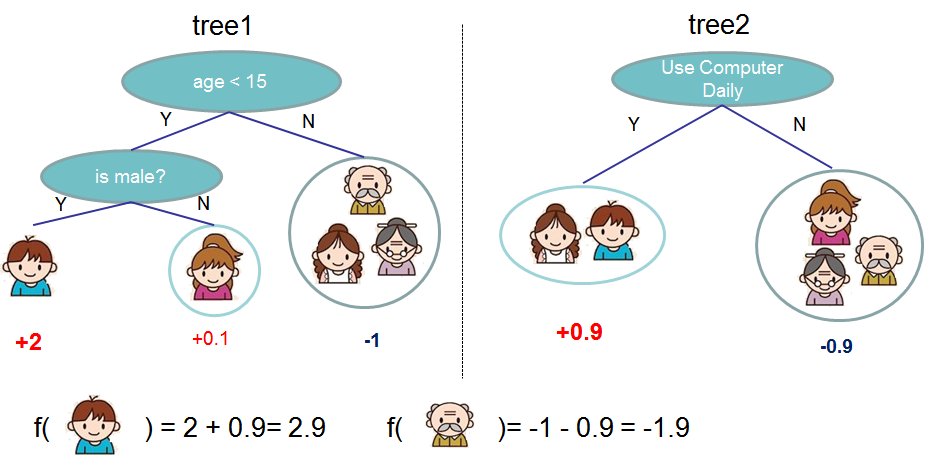
Model: Assuming there are K trees [math]\displaystyle{ \hat y_i = \sum^K_{k=1} f_k(x_I), f_k \in Ƒ }[/math]

Object: [math]\displaystyle{ Obj = \sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k) }[/math]

where [math]\displaystyle{ \sum^n_{i=1}l(y_i,\hat y_i) }[/math] is training loss, [math]\displaystyle{ \sum_{k=1}^K \omega(f_k) }[/math] is complexity of Trees

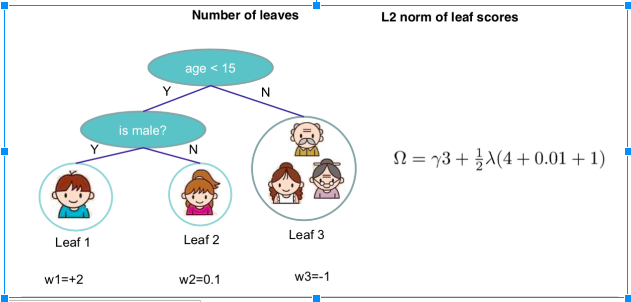
So the target function that needed to optimize is:[math]\displaystyle{ \sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k), f_k \in Ƒ }[/math], where [math]\displaystyle{ \omega(f) = \gamma T+\frac{1}{2}\lambda||w||^2 }[/math]

For example:

Let's look at [math]\displaystyle{ \hat y_i }[/math] [math]\displaystyle{ \hat y{i}^{(0)} = 0 }[/math] [math]\displaystyle{ \hat y{i}^{(1)} = f_1(x_i)=\hat y_i^{(0)}+f_1(x_i) }[/math] [math]\displaystyle{ \hat y{i}^{(2)} = f_1(x_i) + f_2(x_i)=\hat y_i^{(1)}+f_2(x_i) }[/math] ... [math]\displaystyle{ \hat y{i}^{(t)} = \sum^t_{i=1}f_k(x_i)=\hat y_i^{(t-1)}+f_t(x_i) }[/math]