XGBoost: A Scalable Tree Boosting System: Difference between revisions
Jump to navigation
Jump to search
| Line 25: | Line 25: | ||
Model: Assuming there are K trees | Model: Assuming there are K trees | ||
<math>\hat \y_i = \sum^K_{k=1} f_k(x_I), f_k \in Ƒ</math> | <math>\hat \y_i = \sum^K_{k=1} f_k(x_I), f_k \in Ƒ</math> | ||
Objective: <math>Obj = \sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k)</math> | Objective: <math>Obj = \sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k)</math> | ||
where <math>\sum^n_{i=1}l(y_i,\hat y_i)</math> is training loss, <math>\sum_{k=1}^K \omega(f_k)</math> is complexity of Trees | where <math>\sum^n_{i=1}l(y_i,\hat y_i)</math> is training loss, <math>\sum_{k=1}^K \omega(f_k)</math> is complexity of Trees | ||
So <math>\sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k), f_k \in Ƒ</math> is the target function that needed to minimize. | So <math>\sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k), f_k \in Ƒ</math> is the target function that needed to minimize. | ||
First looking at <math>\hat y_i</math> | First looking at <math>\hat y_i</math> | ||
Revision as of 00:23, 22 November 2018
Presented by
- Qianying Zhao
- Hui Huang
- Lingyun Yi
- Jiayue Zhang
- Siao Chen
- Rongrong Su
- Gezhou Zhang
- Meiyu Zhou
2 Tree Boosting In A Nutshell
2.1 Regularized Learning Objective
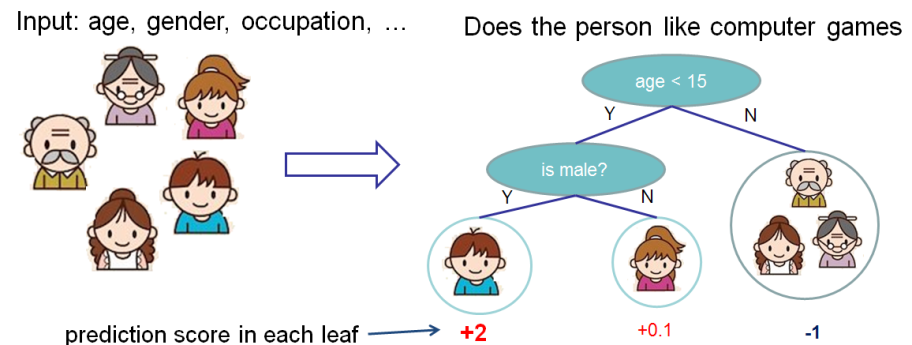
1. Regression Decision Tree (also known as classification and regression tree):
- Decision rules are the same as in decision tree
- Contains one score in each leaf value
2. Model and Parameter
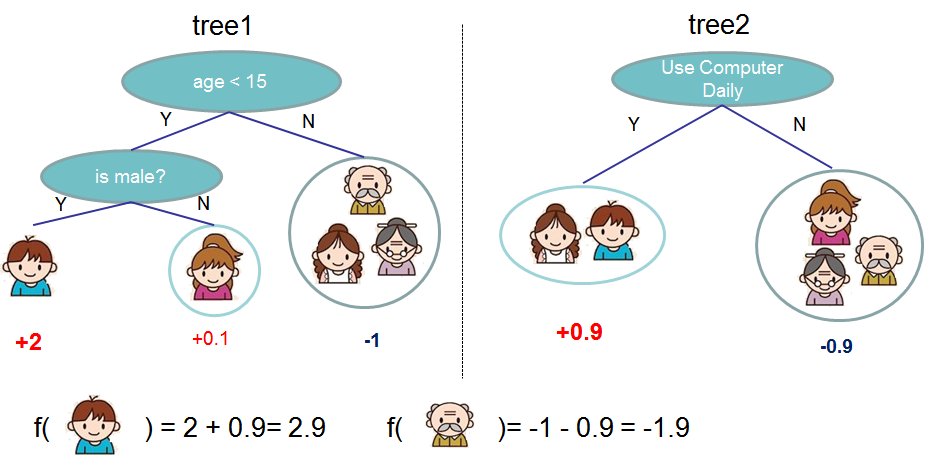
Model: Assuming there are K trees [math]\displaystyle{ \hat \y_i = \sum^K_{k=1} f_k(x_I), f_k \in Ƒ }[/math]
Objective: [math]\displaystyle{ Obj = \sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k) }[/math]
where [math]\displaystyle{ \sum^n_{i=1}l(y_i,\hat y_i) }[/math] is training loss, [math]\displaystyle{ \sum_{k=1}^K \omega(f_k) }[/math] is complexity of Trees So [math]\displaystyle{ \sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k), f_k \in Ƒ }[/math] is the target function that needed to minimize. First looking at [math]\displaystyle{ \hat y_i }[/math]