XGBoost: A Scalable Tree Boosting System

Presented by

• Qianying Zhao
• Hui Huang
• Lingyun Yi
• Jiayue Zhang
• Siao Chen
• Rongrong Su
• Gezhou Zhang
• Meiyu Zhou

2 Tree Boosting In A Nutshell

2.1 Regularized Learning Objective

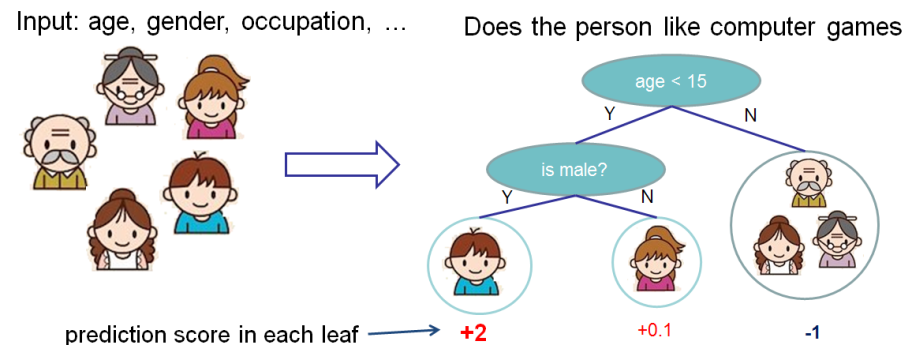
1. Regression Decision Tree (also known as classification and regression tree):

• Decision rules are the same as in decision tree
• Contains one score in each leaf value

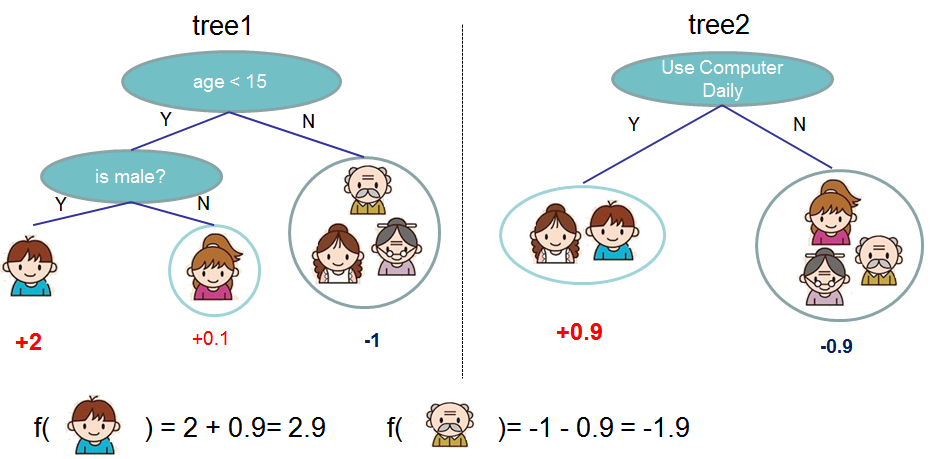
2. Model and Parameter

Model: Assuming there are K trees [math]\displaystyle{ \hat \y_i = \sum^K_{k=1} f_k(x_I), f_k \in Ƒ }[/math] Objective: [math]\displaystyle{ Obj = \sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k) }[/math] where [math]\displaystyle{ \sum^n_{i=1}l(y_i,\hat y_i) }[/math] is training loss, [math]\displaystyle{ \sum_{k=1}^K \omega(f_k) }[/math] is complexity of Trees So [math]\displaystyle{ \sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k), f_k \in Ƒ }[/math] is the target function that needed to minimize. First looking at [math]\displaystyle{ \hat y_i }[/math]