Fairness Without Demographics in Repeated Loss Minimization

This page contains the summary of the paper "Fairness Without Demographics in Repeated Loss Minimization" by Hashimoto, T. B., Srivastava, M., Namkoong, H., & Liang, P. which was published at the International Conference of Machine Learning (ICML) in 2018.

Introduction

Usually, machine learning models are minimized in their average loss to achieve high overall accuracy. While this works well for the majority, minority groups that use the system suffer high error rates because they contribute fewer data to the model. For example, non-native speakers may contribute less to the speech recognizer machine learning model. This phenomenon is known as representation disparity and has been observed in many models that, for instance, recognize faces, or identify the language. This disparity further widens for minority users who suffer higher error rates, as they will lower usage of the system in the future. As a result, minority groups provide even less data for future optimization of the model. With less data points to work with, the disparity becomes even worse - a phenomenon referred to as disparity amplification.

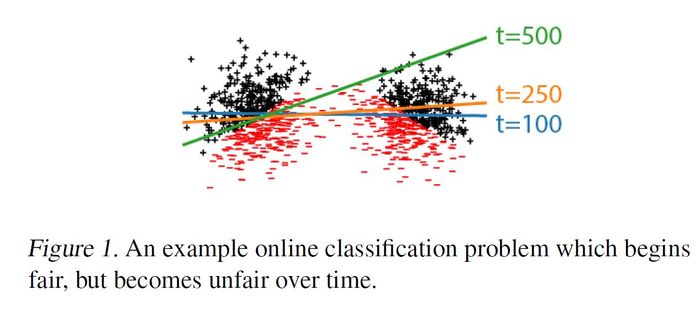
In this paper, Hashimoto et al. provide a strategy for controlling the worst case risk for all groups. They first show that standard empirical risk minimization (ERM) does not control the loss of minority groups, and thus causes representation disparity and its amplification over time (even if the model is fair in the beginning). Second, the researchers try to mitigate this unfairness by proposing the use of distributionally robust optimization (DRO). Indeed, Hashimoto et al. are able to show that DRO can bound the loss for minority groups at every step of time, and is fair for models that ERM turns unfair by applying it to Amazon Mechanical Turk task.

Note on Fairness

Hashimoto et al. follow the difference principle to achieve and measure fairness. It is defined as the maximization of the welfare of the worst-off group, rather than the whole group (cf. utilitarianism).

Related Works

The recent advancements on the topic of fairness in Machine learning can be classified into the following approaches:

1. Rawls Difference principle (Rawls, 2001, p155) - Defines that maximizing the welfare of the worst-off group is fair and stable over time, which increases the chance that minorities will consent to status-quo. The current work builds on this as it sees predictive accuracy as a resource to be allocated.

2. Labels of minorities present in the data:

• Chouldechova, 2017: Use of race (a protected label) in recidivism protection. This study evaluated the likelihood for a criminal defendant to reoffend at a later time, which assisted with criminal justice decision-making. However, a risk assessment instrument called COMPAS was studied and discovered to be biased against black defendants. As the consequences for misclassification can be dire, fairness regarding using race as a label was studied.
• Barocas & Selbst, 2016: Guaranteeing fairness for a protected label through constraints such as equalized odds, disparate impact, and calibration.

In the case specific to this paper, this information is not present.

3. Fairness when minority grouping are not present explicitly

• Dwork et al., 2012 used Individual notions of fairness using fixed similarity function whereas Kearns et al., 2018; Hebert-Johnson et al., 2017 used subgroups of a set of protected labels.
• Kearns et al. (2018); Hebert-Johnson et al. (2017) consider subgroups of a set of protected features.

Again for the specific case in this paper, this is not possible.

4. Online settings

• Joseph et al., 2016; Jabbari et al., 2017 looked at fairness in bandit learning using algorithms compatible with Rawls’ principle on equality of opportunity.
• Liu et al. (2018) analyzed fairness temporally in the context of constraint-based fairness criteria. It showed that fairness is not ensured over time when static fairness constraints are enforced.

Representation Disparity

If a user makes a query [math]\displaystyle{ Z \sim P }[/math], the model [math]\displaystyle{ \theta \in \Theta }[/math] makes a prediction, and the user experiences loss [math]\displaystyle{ \ell (\theta; Z) }[/math].

The expected loss of a model [math]\displaystyle{ \theta }[/math] is denoted as the risk [math]\displaystyle{ \mathcal{R}(\theta) = \mathbb{E}_{Z \sim P} [\ell (\theta; Z)] }[/math].

If input queries are made by users from [math]\displaystyle{ K }[/math] groups, then the distribution over all queries can be re-written as [math]\displaystyle{ Z \sim P := \sum_{k \in [K]} \alpha_kP_k }[/math], where [math]\displaystyle{ \alpha_k }[/math] is the population portion of group [math]\displaystyle{ k }[/math] and [math]\displaystyle{ P_k }[/math] is its individual distribution, and we assume these two variables are unknown.

The risk associated with group [math]\displaystyle{ k }[/math] can be written as, [math]\displaystyle{ \mathcal{R}_k(\theta) := \mathbb{E}_{P_k} [\ell (\theta; Z)] }[/math].

The worst-case risk over all groups can then be defined as, \begin{align} \mathcal{R}_{max}(\theta) := \underset{k \in [K]}{max} \mathcal{R}_k(\theta). \end{align}

Minimizing this function is equivalent to minimizing the risk for the worst-off group.

There is high representation disparity if the expected loss of the model [math]\displaystyle{ \mathcal{R}(\theta) }[/math] is low, but the worst-case risk [math]\displaystyle{ \mathcal{R}_{max}(\theta) }[/math] is high. A model with high representation disparity performs well on average (i.e. has low overall loss), but fails to represent some groups [math]\displaystyle{ k }[/math] (i.e. the risk for the worst-off group is high).

Often, groups are latent and [math]\displaystyle{ k, P_k }[/math] are unknown and the worst-case risks are inaccessible. The technique proposed by Hashimoto et al does not require direct access to these.

Disparity Amplification

Representation disparity can amplify as time passes and loss is minimized. Over [math]\displaystyle{ t = 1, 2, ..., T }[/math] minimization rounds, the group proportions [math]\displaystyle{ \alpha_k^{(t)} }[/math] are not constant, but vary depending on past losses.

At each round the expected number of users [math]\displaystyle{ \lambda_k^{(t+1)} }[/math] from group [math]\displaystyle{ k }[/math] is determined by \begin{align} \lambda_k^{(t+1)} := \lambda_k^{(t)} \nu(\mathcal{R}_k(\theta^{(t)})) + b_k \end{align}

where [math]\displaystyle{ \lambda_k^{(t)} \nu(\mathcal{R}_k(\theta^{(t)})) }[/math] describes the fraction of retained users from the previous optimization, [math]\displaystyle{ \nu(x) }[/math] is a function that decreases as [math]\displaystyle{ x }[/math] increases, and [math]\displaystyle{ b_k }[/math] is the number of new users of group [math]\displaystyle{ k }[/math].

Furthermore, the group proportions [math]\displaystyle{ \alpha_k^{(t)} }[/math], dependent on past losses is defined as: \begin{align} \alpha_k^{(t+1)} := \dfrac{\lambda_k^{(t+1)}}{\sum_{k'\in[K]} \lambda_{k'}^{(t+1)}} \end{align}

To put simply, the number of expected users of a group depends on the number of new users of that group and the fraction of users that continue to use the system from the previous optimization step. If fewer users from minority groups return to the model (i.e. the model has a low retention rate of minority group users), Hashimoto et al. argue that the representation disparity amplifies.

Empirical Risk Minimization (ERM)

Without the knowledge of population proportions [math]\displaystyle{ \alpha_k^{(t)} }[/math], the new user rate [math]\displaystyle{ b_k }[/math], and the retention function [math]\displaystyle{ \nu }[/math] it is hard to control the worst-case risk over all time periods [math]\displaystyle{ \mathcal{R}_{max}^T }[/math]. That is why it is the standard approach to fit a sequence of models [math]\displaystyle{ \theta^{(t)} }[/math] by empirically approximating them. Using ERM, for instance, the optimal model is approached by minimizing the loss of the model:

\begin{align} \theta^{(t)} = arg min_{\theta \in \Theta} \sum_i \ell(\theta; Z_i^{(t)}) \end{align}

However, ERM fails to prevent disparity amplification. By minimizing the expected loss of the model, minority groups experience higher loss (because the loss of the majority group is minimized), and do not return to use the system. In doing so, the population proportions [math]\displaystyle{ \alpha_k^{(t)} }[/math] shift, and certain minority groups contribute even less to the system. This is mirrored in the expected user count [math]\displaystyle{ \lambda^{(t)} }[/math] at each optimization point. In their paper Hashimoto et al. show that, if using ERM, [math]\displaystyle{ \lambda^{(t)} }[/math] is unstable because it loses its fair fixed point (i.e. the population fraction where risk minimization maintains the same population fraction over time). Therefore, ERM fails to control minority risk over time and is considered unfair.

Distributionally Robust Optimization (DRO)

To overcome the unfairness of ERM, Hashimoto et al. developed a distributionally robust optimization (DRO). At this point the goal is still to minimize the worst-case group risk over a single time-step [math]\displaystyle{ \mathcal{R}_{max} (\theta^{(t)}) }[/math] (time steps are omitted in this section's formulas). As previously mentioned, this is difficult to do because neither the population proportions [math]\displaystyle{ \alpha_k }[/math] nor group distributions [math]\displaystyle{ P_k }[/math] are known, which means the data was sampled from different unknown groups. Therefore, in order to improve the performance across different groups, Hashimoto et al. developed an optimization technique that is robust "against all directions around the data generating distribution". This refers to the notion that DRO is robust to any group distribution [math]\displaystyle{ P_k }[/math] whose loss other optimization techniques such as ERM might try to optimize. To create this distributionally robustness, the optimizations risk function [math]\displaystyle{ \mathcal{R}_{dro} }[/math] has to "up-weigh" data [math]\displaystyle{ Z }[/math] that cause high loss [math]\displaystyle{ \ell(\theta, Z) }[/math]. In other words, the risk function has to over-represent mixture components (i.e. group distributions [math]\displaystyle{ P_k }[/math]) in relation to their original mixture weights (i.e. the population proportions [math]\displaystyle{ \alpha_k }[/math]) for groups that suffer high loss.

To do this Hashimoto et al. considered the worst-case loss (i.e. the highest risk) over all perturbations [math]\displaystyle{ P_k }[/math] around [math]\displaystyle{ P }[/math] within a certain limit (because obviously not every outlier should be up-weighed). This limit is described by the [math]\displaystyle{ \chi^2 }[/math]-divergence (i.e. the distance, roughly speaking) between probability distributions. For two distributions [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q }[/math] the divergence is defined as [math]\displaystyle{ D_{\chi^2} (P || Q):= \int (\frac{dP}{dQ} - 1)^2 }[/math]. If [math]\displaystyle{ P }[/math] is not absolutely continuous w.r.t [math]\displaystyle{ Q }[/math], then [math]\displaystyle{ D_{\chi^2} (P || Q):= \infty }[/math]. With the help of the [math]\displaystyle{ \chi^2 }[/math]-divergence, Hashimoto et al. defined the chi-squared ball [math]\displaystyle{ \mathcal{B}(P,r) }[/math] around the probability distribution P. This ball is defined so that [math]\displaystyle{ \mathcal{B}(P,r) := \{Q \ll P : D_{\chi^2} (Q || P) \leq r \} }[/math]. With the help of this ball the worst-case loss (i.e. the highest risk) over all perturbations [math]\displaystyle{ P_k }[/math] that lie inside the ball (i.e. within reasonable range) around the probability distribution [math]\displaystyle{ P }[/math] can be considered. This loss is given by

\begin{align} \mathcal{R}_{dro}(\theta, r) := \underset{Q \in \mathcal{B}(P,r)}{sup} \mathbb{E}_Q [\ell(\theta;Z)] \end{align}

which for [math]\displaystyle{ P:= \sum_{k \in [K]} \alpha_k P_k }[/math] for all models [math]\displaystyle{ \theta \in \Theta }[/math] where [math]\displaystyle{ r_k := (1/a_k -1)^2 }[/math] bounds the risk [math]\displaystyle{ \mathcal{R}_k(\theta) \leq \mathcal{R}_{dro} (\theta; r_k) }[/math] for each group with risk [math]\displaystyle{ \mathcal{R}_k(\theta) }[/math]. Furthermore, if the lower bound on the group proportions [math]\displaystyle{ \alpha_{min} \leq min_{k \in [K]} \alpha_k }[/math] is specified, and the radius is defined as [math]\displaystyle{ r_{max} := (1/\alpha_{min} -1)^2 }[/math], the worst-case risk [math]\displaystyle{ \mathcal{R}_{max} (\theta) }[/math] can be controlled by [math]\displaystyle{ \mathcal{R}_{dro} (\theta; r_{max}) }[/math] by forming an upper bound that can be minimized.

Optimization of DRO

To minimize [math]\displaystyle{ \mathcal{R}_{dro}(\theta, r) := \underset{Q \in \mathcal{B}(P,r)}{sup} \mathbb{E}_Q [\ell(\theta;Z)] }[/math] Hashimoto et al. look at the dual of this maximization problem (i.e. every maximization problem can be transformed into a minimization problem and vice-versa). This dual is given by the minimization problem

\begin{align} \mathcal{R}_{dro}(\theta, r) = \underset{\eta \in \mathbb{R}}{inf} \left\{ F(\theta; \eta):= C\left(\mathbb{E}_P \left[ [\ell(\theta;Z) - \eta]_+^2 \right] \right)^\frac{1}{2} + \eta \right\} \end{align}

with [math]\displaystyle{ C = (2(1/a_{min} - 1)^2 + 1)^{1/2} }[/math]. [math]\displaystyle{ \eta }[/math] describes the dual variable (i.e. the variable that appears in creating the dual). Since [math]\displaystyle{ F(\theta; \eta) }[/math] involves an expectation [math]\displaystyle{ \mathbb{E}_P }[/math] over the data generating distribution [math]\displaystyle{ P }[/math], [math]\displaystyle{ F(\theta; \eta) }[/math] can be directly minimized. For convex losses [math]\displaystyle{ \ell(\theta;Z) }[/math], [math]\displaystyle{ F(\theta; \eta) }[/math] is convex, and can be minimized by performing a binary search over [math]\displaystyle{ \eta }[/math]. In their paper, Hashimoto et al. further show that optimizing [math]\displaystyle{ \mathcal{R}_{dro}(\theta, r_{max}) }[/math] at each time step controls the future worst-case risk [math]\displaystyle{ \mathcal{R}_{max} (\theta) }[/math], and therefore retention rates. That means if the initial group proportions satisfy [math]\displaystyle{ \alpha_k^{(0)} \geq a_{min} }[/math], and [math]\displaystyle{ \mathcal{R}_{dro}(\theta, r_{max}) }[/math] is optimized for every time step (and therefore [math]\displaystyle{ \mathcal{R}_{max} (\theta) }[/math] is minimized), [math]\displaystyle{ \mathcal{R}_{max}^T (\theta) }[/math] over all time steps is controlled. In other words, optimizing [math]\displaystyle{ \mathcal{R}_{dro}(\theta, r_{max}) }[/math] every time step is enough to avoid disparity amplification.

Pros of DRO: In many cases, the expected value is a good measure of performance Cons of DRO: One has to know the exact distribution of the underlying distribution to perform the stochastic optimization. Deviant from the assumed distribution may result in sub-optimal solutions. The paper makes strong assumptions on [math]\displaystyle{ \mathcal{P} }[/math] with respect to group allocations, and thus requires a high amount of data to optimize; when assumptions are violated, the algorithm fails to perform as intended.

Critiques

This paper works on representational disparity which is a critical problem to contribute to. The methods are well developed and the paper reads coherently. However, the authors have several limiting assumptions that are not very intuitive or scientifically suggestive. The first assumption is that the [math]\displaystyle{ \eta }[/math] function denoting the fraction of users retained is differentiable and strictly decreasing function. This assumption does not seem practical. The second assumption is that the learned parameters are having a Poisson distribution. There is no explanation of such an assumption and reasons hinted at are hand-wavy at best. Though the authors are building a case against the Empirical risk minimization method, this method is exactly solvable when the data is linearly separable. The DRO method is computationally more complex than ERM and is not entirely clear if it will always have an advantage for a different class of problems.

Other Sources

1. [1] is a easy-to-read paper description.

References

Rawls, J. Justice as fairness: a restatement. Harvard University Press, 2001.

Barocas, S. and Selbst, A. D. Big data’s disparate impact. 104 California Law Review, 3:671–732, 2016.

Chouldechova, A. A study of bias in recidivism prediciton instruments. Big Data, pp. 153–163, 2017

Dwork, C., Hardt, M., Pitassi, T., Reingold, O., and Zemel, R. Fairness through awareness. In Innovations in Theoretical Computer Science (ITCS), pp. 214–226, 2012.

Kearns, M., Neel, S., Roth, A., and Wu, Z. S. Preventing fairness gerrymandering: Auditing and learning for subgroup fairness. arXiv preprint arXiv:1711.05144, 2018.

Hebert-Johnson, ´ U., Kim, M. P., Reingold, O., and Roth-blum, G. N. Calibration for the (computationallyidentifiable) masses. arXiv preprint arXiv:1711.08513, 2017.

Joseph, M., Kearns, M., Morgenstern, J., Neel, S., and Roth, A. Rawlsian fairness for machine learning. In FATML, 2016.

Jabbari, S., Joseph, M., Kearns, M., Morgenstern, J., and Roth, A. Fairness in reinforcement learning. In International Conference on Machine Learning (ICML), pp. 1617–1626, 2017.

Liu, L. T., Dean, S., Rolf, E., Simchowitz, M., and Hardt, M. Delayed impact of fair machine learning. arXiv preprint arXiv:1803.04383, 2018.