Reinforcement Learning of Theorem Proving

Introduction

Automated reasoning over mathematical proof was a major motivation for the development of computer science. Automated theorem provers (ATP) can in principle be used to attack any formally stated mathematical problem, and is a research area that has been studied since the early 20th century. [1] As of today, state-of-art ATP systems rely on fast implementation of complete proof calculi. such as resolution and tableau. However, they are still far weaker than trained mathematicians. Within current ATP systems, many heuristics are essential for their performance. As a result, in recent years machine learning has been used to replace such heuristics and improve the performance of ATPs.

In this paper the authors implemented a reinforcement learning based ATP, rlCoP. The proposed ATP reasons within first-order logic. The underlying proof calculi is the connection calculi [2], and the reinforcement learning method is Monte Carlo tree search along with policy and value learning. It was shown that reinforcement learning results in a 42.1% performance increase compared to the base prover (without learning).

Related Work

C. Kalizyk and J. Urban proposed a supervised learning based ATP, FEMaLeCoP, whose underlying proof calculi is the same as this paper in 2015. [3] In their algorithm learns from existing proofs to choose the next tableau extension step. Similarly, S. Loos, et al. developed an supervised learning ATP system in 2017 [4], with superposition as their proof calculi. However they chose deep neural network (CNNs and RNNs) as feature extractor.

On a different note, A. Alemi, et al. proposed a deep sequence model for premise selection in 2016 [5], and they claim to be the first team to involve deep neural networks in ATPs. Although premise selection is not directly linked to automated reasoning, it is still an important component in ATPs, and their paper provides some insights about how to process datasets of formally stated mathematical problems.

First Order Logic and Connection Calculi

Here we assume basic first-order logic and theorem proving terminology, and we will offer a brief introduction of the base prover and connection calculi. For example, let us try to prove the following first-order sentence.

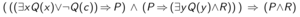
This sentence can be transformed into a formula in Skolemized DNF form.

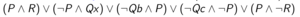
The original first-order sentence is valid if and only if the Skolemized DNF formula is a tautology. The connection calculi attempts to show that the Skolemized DNF formula is a tautology by constructing a tableaux. You will start at the special node, root, which is an open leaf. At each step, you select a clause (for example, clause [math]\displaystyle{ P \wedge R }[/math] is selected in the first step), and add the literals as children for an existing open leaf. For every open leaf, examine the path from root to this leaf. If two literals on this path is unifiable (for example, [math]\displaystyle{ Qx' }[/math] is unifiable with [math]\displaystyle{ \neg Qc }[/math]), this leaf is then closed. In standard terminology it states that a connection is found on this branch.

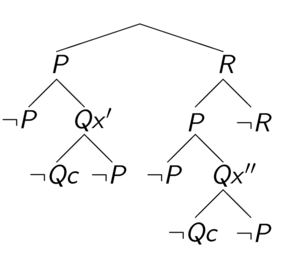
Our goal is to close every leaf, i.e. on every branch, there exists a connection. If such state is reached, we have showed that the Skolemized DNF formula is a tautology, thus proving the original first-order sentence. As we can see from the constructed tableaux, the example sentence is indeed valid.

References

[1] C. Kaliszyk, et al. Reinforcement Learning of Theorem Proving. NIPS 2018.

[2] J. Otten and W. Bibel. leanCoP: Lean Connection-Based Theorem Proving. Journal of Symbolic Computation, vol. 36, pp. 139-161, 2003.

[3] C. Kaliszyk and J. Urban. FEMaLeCoP: Fairly Efficient Machine Learning Connection Prover. Lecture Notes in Computer Science. vol. 9450. pp. 88-96, 2015.

[4] S. Loos, et al. Deep Network Guided Proof Search. LPAR-21, 2017.

[5] A. Alemi, et al. DeepMath-Deep Sequence Models for Premise Selection. NIPS 2016.