Zero-Shot Visual Imitation: Difference between revisions
| Line 25: | Line 25: | ||
{{NumBlk|:|<math>a_τ =π(x_i,x_g;θ_π)</math>|{{EquationRef|1}}}} | {{NumBlk|:|<math>a_τ =π(x_i,x_g;θ_π)</math>|{{EquationRef|1}}}} | ||
{{NumBlk|:|<math>y=ax+b</math>|Eq. 3}} | |||
===Forward Consistency Loss=== | ===Forward Consistency Loss=== | ||
Revision as of 13:41, 3 November 2018
This page contains a summary of the paper "Zero-Shot Visual Imitation" by Pathak, D., Mahmoudieh, P., Luo, G., Agrawal, P. et al. It was published at the International Conference on Learning Representations (ICLR) in 2018.
Introduction
The dominant paradigm for imitation learning relies on strong supervision of expert actions to learn both what and how to imitate for a certain task. For example, in the robotics field, Learning from Demonstration (LfD) (Argall et al., 2009; Ng & Russell, 2000; Pomerleau, 1989; Schaal, 1999) requires an expert to manually move robot joints (kinesthetic teaching) or teleoperate the robot to teach a desired task. The expert will, in general, provide multiple demonstrations of a specific task at training time which the agent will form into observation-action pairs to then distill into a policy for performing the task. In the case of demonstrations for a robot, this heavily supervised process is tedious and unsustainable especially looking at the fact that new tasks need a set of new demonstrations for the robot to learn from.
Observational Learning (Bandura & Walters, 1977), a term from the field of psychology, suggests a more general formulation where the expert communicates what needs to be done (as opposed to how something is to be done) by providing observations of the desired world states via video or sequential images. This is the proposition of the paper and while this is a harder learning problem, it is possibly more useful because the expert can now distill a large number of tasks easily (and quickly) to the agent.
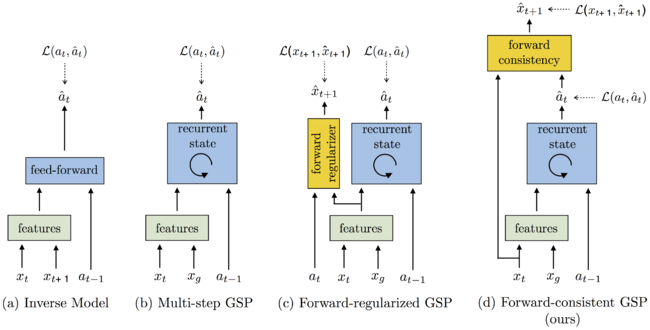
Learning the Goal-Conditioned Skill Policy (GSP)
[math]\displaystyle{ S : \{x_1, a_1, x_2, a_2, ..., x_T\} }[/math]
[math]\displaystyle{ a = π_E(s) }[/math]
[math]\displaystyle{ (x_i,x_g) }[/math]
[math]\displaystyle{ (\overrightarrow{a}_τ : a_1,a_2...a_K) }[/math]
[math]\displaystyle{ (x_g) }[/math]
[math]\displaystyle{ (x_i) }[/math]