Learning to Teach

Introduction

This paper proposed the "learning to teach" (L2T) framework with two intelligent agents: a student model/agent, corresponding to the learner in traditional machine learning algorithms, and a teacher model/agent, determining the appropriate data, loss function, and hypothesis space to facilitate the learning of the student model.

In modern human society, the role of teaching is heavily implicated in our education system, the goal being to equip students with necessary knowledge and skills in an efficient manner. This is the fundamental student and teacher framework on which education stands. However, in the field of artificial intelligence and specifically machine learning, researchers have focused most of their efforts on the student ie. designing various optimization algorithms to enhance the learning ability of intelligent agents. The paper argues that a formal study on the role of ‘teaching’ in AI is required. Analogous to teaching in human society, the teaching framework can select training data which corresponds to choosing the right teaching materials (e.g. textbooks); designing the loss functions corresponding to setting up targeted examinations; defining the hypothesis space corresponds to imparting the proper methodologies. Furthermore, an optimization framework (instead of heuristics) should be used to update the teaching skills based on the feedback from students, so as to achieve teacher-student co-evolution.

Related Work

The L2T framework connects with two emerging trends in machine learning. The first is the movement from simple to advanced learning. This includes meta learning (Schmidhuber, 1987; Thrun & Pratt, 2012) which explores automatic learning by transferring learned knowledge from meta tasks [1]. This approach has been applied to few-shot learning scenarios and in designing general optimizers and neural network architectures.

The second is the teaching which can be classified into machine-teaching (Zhu, 2015) [2] and hardness based methods . The former seeks to construct a minimal training set for the student to learn a target model (ie. an oracle). The latter assumes an order of data from easy instances to hard ones, hardness being determined in different ways. In curriculum learning (CL) (Bengio et al, 2009; Spitkovsky et al. 2010; Tsvetkov et al, 2016) [3] measures hardness through heuristics of the data while self-paced learning (SPL) (Kumar et al., 2010; Lee & Grauman, 2011; Jiang et al., 2014; Supancic & Ramanan, 2013) [4] measures hardness by loss on data.

The limitations of these works boil down to a lack of formally defined teaching problem as well as the reliance on heuristics and fixed rules for teaching which hinders generalization of the teaching task.

Learning to Teach

To introduce the problem and framework, without loss of generality, consider the setting of supervised learning.

Problem Definition

The student model, denoted μ(), takes input: the set of training data [math]\displaystyle{ D }[/math], the function class [math]\displaystyle{ Ω }[/math], and loss function [math]\displaystyle{ L }[/math] to output a function, [math]\displaystyle{ f(ω) }[/math], with parameter [math]\displaystyle{ ω^* }[/math] which minimizes risk [math]\displaystyle{ R(ω) }[/math]

The teaching model, denoted φ, tries to provide [math]\displaystyle{ D }[/math], [math]\displaystyle{ L }[/math], and [math]\displaystyle{ Ω }[/math] (or any combination, denoted [math]\displaystyle{ A }[/math]) to the student model such that the student model either achieves lower risk R(ω) or progresses as fast as possible.

Training Data: Outputting a good training set D, analogous to human teachers providing students with proper learning materials such as textbooks

Loss Function: Designing a good loss function [math]\displaystyle{ L }[/math] , analogous to providing useful assessment criteria for students.

Hypothesis Space: Defining a good function class [math]\displaystyle{ Ω }[/math] which the student model can select from. This is analogous to human teachers providing appropriate context, eg. middle school students taught math with basic algebra while undergraduate students are taught with calculus.

Framework

The training phase consists of the teacher providing the student with the subset [math]\displaystyle{ A_{train} }[/math] of [math]\displaystyle{ A }[/math] and then taking feedback to improve its own parameters. The L2T process is outlined in figure below:

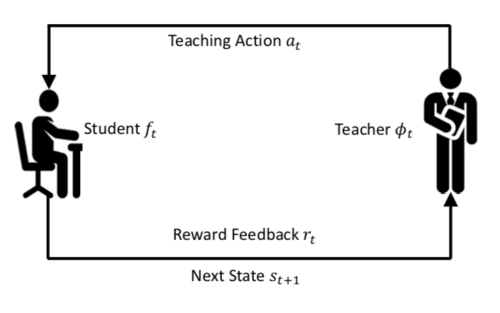
• [math]\displaystyle{ s_t ∈ S }[/math] represents information available to the teacher model at time [math]\displaystyle{ t }[/math]
• [math]\displaystyle{ a_t ∈ A }[/math] represents action taken the teacher model at time [math]\displaystyle{ t }[/math]. Can be any combination of teaching tasks involving the training data, loss function, and hypothesis space.
• [math]\displaystyle{ φ_θ : S → A }[/math] is policy used by teach moderl to generate action [math]\displaystyle{ φ_θ(s_t) = a_t }[/math]
• Student model takes [math]\displaystyle{ a_t }[/math] as input and outputs function [math]\displaystyle{ f_t }[/math]

Once the training process converges, the teacher model may be utilized to teach a different subset of [math]\displaystyle{ A }[/math] or teach a different student model.

Application

The paper applies data teaching to a variety of

D, L and Ω (or any combination, denoted [math]\displaystyle{  A  }[/math])