Spherical CNNs

WORK IN PROGRESS********************************************************************************************************************

Introduction

Convolutional Neural Networks (CNNs), or network architectures involving CNNs, are the current state of the art for learning 2D image processing tasks such as semantic segmentation and object detection. CNNs work well in large part due to the property of being translationally invariant when combined with max pooling. This property allows a network trained to detect a certain type of object to still detect the object even if it is translated to another position in the image.

Notation

Below are listed several important terms:

• [math]\displaystyle{ S^2 }[/math] Sphere - The two dimensional surface from an ordinary 3D sphere
• SO(3) - A three-dimensional manifold which consists of 3D rotations

Experiments

The authors provide several experiments. The first set of experiments are designed to show the numerical stability and accuracy of the outlined methods. The second group of experiments demonstrates how the algorithms can be applied to current problem domains.

Equivariance Error

In this experiment the authors try to show experimentally that their theory of equivariance holds. They express their doubts that the equivariance would hold due to potential discretization artifacts. The experiment is set up by first testing the equivariance of the SO(3) correlation at different resolutions. 500 random rotations and feature maps (with 10 channels) are sampled. They then calculate [math]\displaystyle{ \small\Delta = \dfrac{1}{n} \sum_{i=1}^n std(L_{R_i} \Phi(f_i) - \phi(L_{R_i} f_i))/std(\Phi(f_i)) }[/math] Note: The authors do not mention what the std function is however it is likely the standard deviation function as 'std' is the command for standard deviation in MATLAB. [math]\displaystyle{ \Phi }[/math] is a composition of SO(3) correlation layers with filters which have been randomly initialized. The authors mention that they were expecting [math]\displaystyle{ \Delta }[/math] to be zero in the case of perfect equivariance. The is due to, as proven earlier, the following two terms equalling each other in the continuous case: [math]\displaystyle{ \small L_{R_i} \Phi(f_i) - \phi(L_{R_i} f_i) }[/math]. The results are shown in Figure 3.

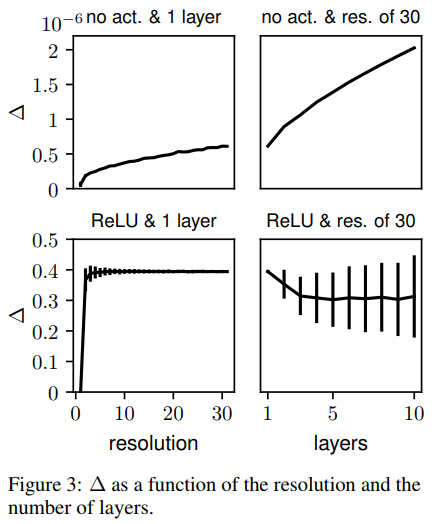
[math]\displaystyle{ \Delta }[/math] only grows with resolution/layers when there is no activation function. With ReLU activation the error stays constant once slightly higher than 0 resolution. The authors indicate that the error must therefore be from the feature map rotation since this type of error is exact only for bandlimited functions.

MNIST Data

The experiment using MNIST data was created by projecting MNIST digits onto a sphere using stereographic projection to create the resulting images as seen in Figure 4.

The authors created two datasets, one with the projected digits and the other with the same projected digits which were then subjected to a random rotation. The spherical CNN architecture used was [math]\displaystyle{ \small S^2 }[/math]conv-ReLU-SO(3)conv-ReLU-FC-softmax and was attempted with bandwidths of 30,10,6 and 20,40,10 channels for each layer respectively. This model was compared to a baseline CNN with layers conv-ReLU-conv-ReLU-FC-softmax with 5x5 filters, 32,64,10 channels and stride of 3. For comparison this leads to approximately 68K parameters for the baseline and 58K parameters for the spherical CNN. Results can be seen in Table 1. It is clear from the results that the spherical CNN architecture made the network rotationally invariant. Performance on the rotated set is almost identical to the non-rotated set, even when trained on the non-rotated set. Compare this to the non-spherical architecture which becomes unusable when rotating the digits.

SHREC17

The SHREC dataset contains 3D models from the ShapeNet dataset which are classified into categories. It consists of a regularly aligned dataset and a rotated dataset. The models from the SHREC17 dataset were projected onto a sphere by means of raycasting. Different properties of the objects obtained from the raycast of the original model and the convex hull of the model make up the different channels which are input into the spherical CNN.

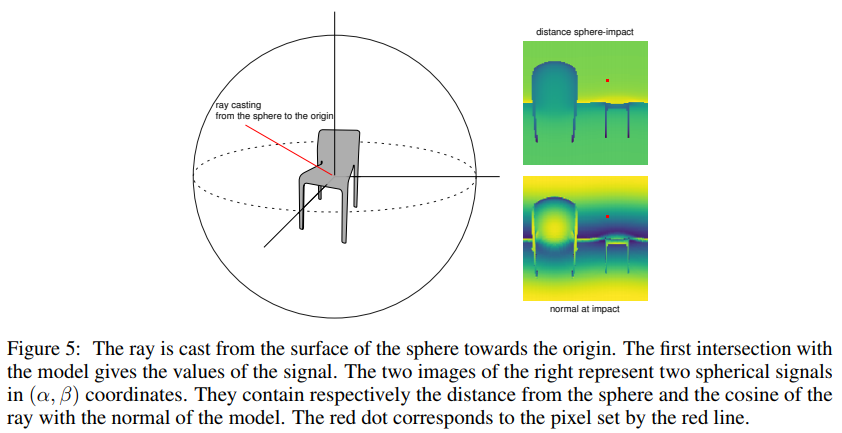
The network architecture used is an initial [math]\displaystyle{ \small S^2 }[/math]conv-BN-ReLU block which is followed by two SO(3)conv-BN-ReLU blocks. The output is then fed into a MaxPool-BN block then a linear layer to the output for final classification.

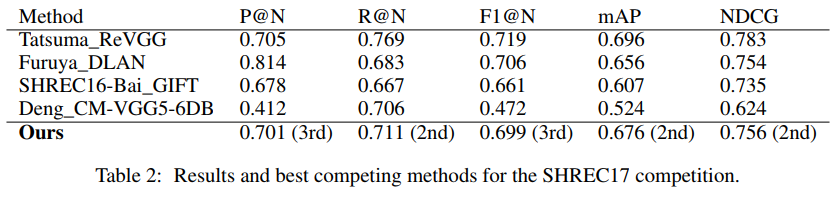
This architecture achieves state of the art results on the 2017 tasks. The model places 2nd or 3rd in all categories but was not submitted as the 2017 task is closed. Table 2 shows the comparison of results with the top 3 submissions in each category. The authors claim the results show empirical proof of the usefulness of spherical CNNs. They elaborate that this is largely due to the fact that most architectures on the SHREC17 competition are highly specialized whereas their model is fairly general.

Molecular Atomization

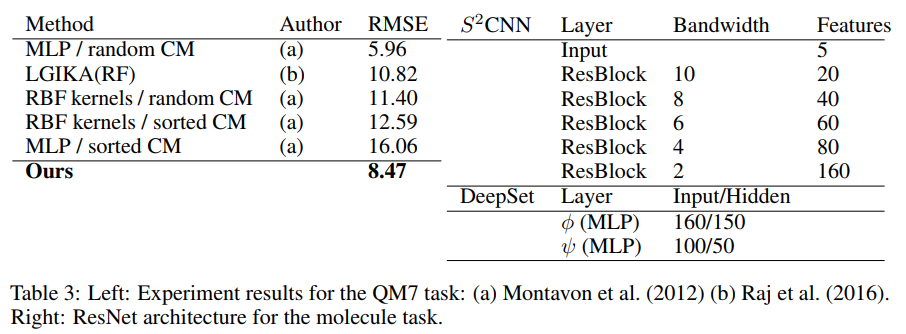
In this experiment a spherical CNN is implemented with an architecture resembling that of ResNet. The architecture for this experiment has ~1.4M parameters, far exceeding the scale of the spherical CNNs in the other experiments. They use the QM7 dataset which has the task of predicting atomization energy of molecules. The positions and charges given in the dataset are projected onto the sphere using potential functions. A summary of their results is shown in Table 3 along with some of the spherical CNN architecture details. It shows the different RMSE obtained from different methods. The results from this final experiment also seem to be promising as the network the authors present achieves the second best score. They also note that the first place method grows exponentially with the number of atoms per molecule so is unlikely to scale well.

Critiques

The reviews on Spherical CNNs were very positive and it is ranked in the top 1% of papers submitted to ICLR 2018. Positive points were the novelty of the architecture, the wide variety of experiments performed, and the writing. One original critique was that the related works section only lists previous methods and that a description of the methods would have provided more clarity. The authors have since expanded the section however it is still limited which they attribute to length limitations. Another critique is that the evaluation does not provide enough depth.

Source Code

Source code is available at: https://github.com/jonas-koehler/s2cnn