STAT946F17/ Dance Dance Convolution

Introduction

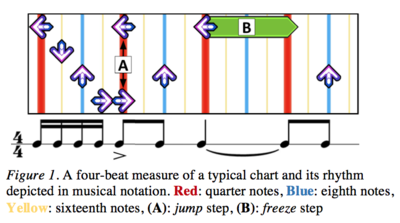
• Dance Dance Revolution (DDR)

Dance Dance Revolution (DDR) is a rhythm-based video game. Players perform steps on a dance platform in synchronization with music as directed by on-screen step charts. The dance pad contains up, down, left, and right arrows, each of which can be in one of four states: on, off, hold, or release. There are $4^4 = 256$ possible step combinations at any instant since the four arrows can be in any of the four states independently. The terms jump: hitting two or more arrows at once; freeze: holding on one arrow for some duration. (Figure 1 (A) & (B))

Step charts exhibit complex semantics and tend to mirror musical structure: particular sequences of steps correspond to different motifs and reoccur as sections of the song are repeated. (Figure 1) The DDR community uses simulators, such as the opensource StepMania, which allow fans to create their own charts. Typically, for each song, packs containing one chart for five difficulty levels are created.

Figure 2. Proposed learning to choreograph pipeline for four seconds of the song Knife Party feat. Mistajam - Sleaze. The pipeline ingests audio features (Bottom) and produces a playable DDR choreography (Top) corresponding to the audio.

• Learning to Choreograph

While players may grow tired of existing charts in standardized packs or creating charts can be really time-consuming for players, the authors introduce the task of learning to choreograph, which learns to produce new step charts given raw audio tracks. This task has been approached via ad-hoc method, it is the first time to be casted as a learning task to mimic the semantics of human-generated charts. The learning task is broke into two subtasks: First, step placement task decides when to place steps conditioning on various diffculty levels. Second, step selection task decides which steps to select at each timestamp.

• Music Information Retrieval (MIR)

Music information retrieval (MIR) may be involved in the progress on learning to choreograph. 1) step placement task closely resembles onset detection, a well-studied MIR problem. Onset detection identifies the times of all musically salient events, such as melody notes or drum strikes and each DDR step corresponds to an onset.

2) DDR packs specify a metronome click track for each song. For songs with changing tempos, the location of change and the new tempo are annotated. This click data could help for beat tracking and tempo detection.

• Contributions

1) Defining learning to choreograph, a new task with real-world usefulness and strong connections to fundamental problems in MIR.

2) Introducing two large, curated datasets for benchmarking DDR choreography algorithms.

3) Presenting an effective pipeline for learning to choreograph with deep neural networks.

Data

Basic statistics of the two datasets are shown in Table 1.

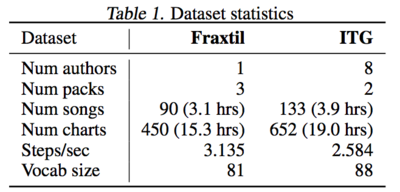
• Notes from Table 1:

1) Fraxtil: single author vs. In The Groove (ITG): multi-author

2) Each dataset contains five charts per song corresponding to increasing difficulty levels except that ITG dataset has 13 songs that lack charts for the highest difficulty.

3) The two datasets have similar vocabulary sizes (81 and 88 distinct step combinations, respectively).

4) The datasets contain around 35 hours of annotations and 350,000 steps considering all charts across all songs.

• Data Augmentation:

Four instances of each chart, by mirroring left/right, up/down (or both), are generated to augment the amount of data available for training.

• (beat, time, step) tuples:

To make the data easier to work with, the authors convert the useful data correspoding to the metadata to a canonical form consisting of (beat, time, step) tuples.

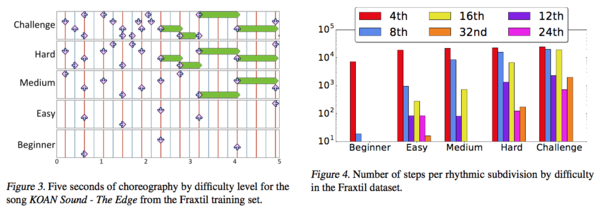
• Number of steps per rhythmic subdivision by difficulty (Figure4)

An increase in difficulty corresponds to increasing trend for steps to appear at finer rhythmic subdivisions.

Methods

Pipeline: 1) extract an audio feature representation

2) feed this representation into a step placement algorithm, which estimates probabilities that a step lies within that frame

3) use a peak-picking process on this sequence of probabilities to identify the precise timestamps at which to place steps

4) given a sequence of timestamps, use a step selection algorithm to choose which steps to place at each time. Note the approach to this problem involves modeling the probability distribution $\mathbb{P}(m_n|m_{n-1},...,m_1)$, where $m_{n}$ is the $n^{th}$ step in the sequence.