Modular Multitask Reinforcement Learning with Policy Sketches

Introduction

STILL EDITING. DO NOT MAKE CHANGES=

This paper describes a framework for learning compos-able deep subpolicies in a multitask setting, guided only by abstract sketches of high-level behavior. General rein-forcement learning algorithms allow agents to solve tasks in complex environments. But tasks featuring extremely delayed rewards or other long-term structure are often dif-ficult to solve with flat, monolithic policies, and a long line of prior work has studied methods for learning hier-archical policy representations (Sutton et al., 1999; Diet-terich, 2000; Konidaris & Barto, 2007; Hauser et al., 2008). While unsupervised discovery of these hierarchies is possi-ble (Daniel et al., 2012; Bacon & Precup, 2015), practical approaches often require detailed supervision in the form of explicitly specified high-level actions, subgoals, or be-havioral primitives (Precup, 2000). These depend on state representations simple or structured enough that suitable reward signals can be effectively engineered by hand.

But is such fine-grained supervision actually necessary to achieve the full benefits of hierarchy? Specifically, is it necessary to explicitly ground high-level actions into the representation of the environment? Or is it sufficient to simply inform the learner about the abstract structure of policies, without ever specifying how high-level behaviors should make use of primitive percepts or actions?

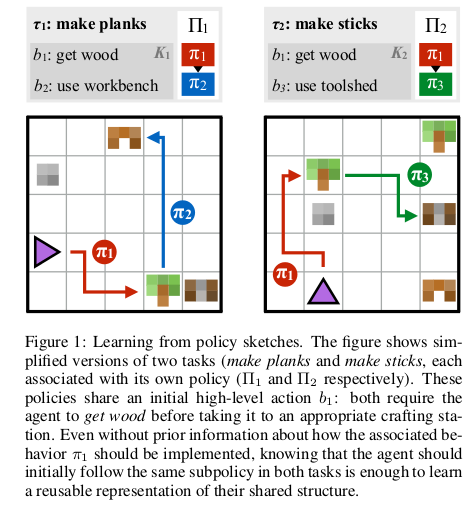
To answer these questions, we explore a multitask re-inforcement learning setting where the learner is pre-sented with policy sketches. Policy sketches are short, un-grounded, symbolic representations of a task that describe its component parts, as illustrated in Figure 1. While sym-bols might be shared across tasks (get wood appears in sketches for both the make planks and make sticks tasks), the learner is told nothing about what these symbols mean, in terms of either observations or intermediate rewards.

We present an agent architecture that learns from policy sketches by associating each high-level action with a pa-rameterization of a low-level subpolicy, and jointly op-timizes over concatenated task-specific policies by tying parameters across shared subpolicies. We find that this architecture can use the high-level guidance provided by sketches, without any grounding or concrete definition, to dramatically accelerate learning of complex multi-stage be-haviors. Our experiments indicate that many of the benefits to learning that come from highly detailed low-level su-pervision (e.g. from subgoal rewards) can also be obtained from fairly coarse high-level supervision (i.e. from policy sketches). Crucially, sketches are much easier to produce: they require no modifications to the environment dynam-ics or reward function, and can be easily provided by non-experts. This makes it possible to extend the benefits of hierarchical RL to challenging environments where it may not be possible to specify by hand the details of relevant subtasks. We show that our approach substantially outper-forms purely unsupervised methods that do not provide the learner with any task-specific guidance about how hierar-chies should be deployed, and further that the specific use of sketches to parameterize modular subpolicies makes bet-ter use of sketches than conditioning on them directly.

The present work may be viewed as an extension of recent approaches for learning compositional deep architectures from structured program descriptors (Andreas et al., 2016; Reed & de Freitas, 2016). Here we focus on learning in in-teractive environments. This extension presents a variety of technical challenges, requiring analogues of these methods that can be trained from sparse, non-differentiable reward signals without demonstrations of desired system behavior.

Our contributions are:

A general paradigm for multitask, hierarchical, deep reinforcement learning guided by abstract sketches of task-specific policies.

A concrete recipe for learning from these sketches, built on a general family of modular deep policy rep-resentations and a multitask actor–critic training ob-jective.

The modular structure of our approach, which associates every high-level action symbol with a discrete subpolicy, naturally induces a library of interpretable policy fragments.that are easily recombined. This makes it possible to eval-uate our approach under a variety of different data condi-tions: (1) learning the full collection of tasks jointly via reinforcement, (2) in a zero-shot setting where a policy sketch is available for a held-out task, and (3) in a adapta-tion setting, where sketches are hidden and the agent must learn to adapt a pretrained policy to reuse high-level ac-tions in a new task. In all cases, our approach substantially outperforms previous approaches based on explicit decom-position of the Q function along subtasks (Parr & Russell, 1998; Vogel & Jurafsky, 2010), unsupervised option dis-covery (Bacon & Precup, 2015), and several standard pol-icy gradient baselines.

We consider three families of tasks: a 2-D Minecraft-inspired crafting game (Figure 3a), in which the agent must acquire particular resources by finding raw ingredients, combining them together in the proper order, and in some cases building intermediate tools that enable the agent to al-ter the environment itself; a 2-D maze navigation task that requires the agent to collect keys and open doors, and a 3-D locomotion task (Figure 3b) in which a quadrupedal robot must actuate its joints to traverse a narrow winding cliff.

In all tasks, the agent receives a reward only after the final goal is accomplished. For the most challenging tasks, in-volving sequences of four or five high-level actions, a task-specific agent initially following a random policy essen-tially never discovers the reward signal, so these tasks can-not be solved without considering their hierarchical struc-ture. We have released code at http://github.com/ jacobandreas/psketch.

Related Work

The agent representation we describe in this paper be-longs to the broader family of hierarchical reinforcement learners. As detailed in Section 3, our approach may be viewed as an instantiation of the options framework first described by Sutton et al. (1999). A large body of work describes techniques for learning options and related ab-stract actions, in both single- and multitask settings. Most techniques for learning options rely on intermediate su-pervisory signals, e.g. to encourage exploration (Kearns & Singh, 2002) or completion of pre-defined subtasks (Kulka-rni et al., 2016). An alternative family of approaches em-ploys post-hoc analysis of demonstrations or pretrained policies to extract reusable sub-components (Stolle & Pre-cup, 2002; Konidaris et al., 2011; Niekum et al., 2015). Techniques for learning options with less guidance than the present work include Bacon & Precup (2015) and Vezhn-evets et al. (2016), and other general hierarchical policy learners include Daniel et al. (2012), Bakker & Schmidhu-ber (2004) and Menache et al. (2002). We will see that the minimal supervision provided by policy sketches re-sults in (sometimes dramatic) improvements over fully un-supervised approaches, while being substantially less oner-ous for humans to provide compared to the grounded su-pervision (such as explicit subgoals or feature abstraction hierarchies) used in previous work.

Once a collection of high-level actions exists, agents are faced with the problem of learning meta-level (typically semi-Markov) policies that invoke appropriate high-level actions in sequence (Precup, 2000). The learning problem we describe in this paper is in some sense the direct dual to the problem of learning these meta-level policies: there, the agent begins with an inventory of complex primitives and must learn to model their behavior and select among them; here we begin knowing the names of appropriate high-level actions but nothing about how they are imple-mented, and must infer implementations (but not, initially, abstract plans) from context. Our model can be combined with these approaches to support a “mixed” supervision condition where sketches are available for some tasks but not others (Section 4.5).

Another closely related line of work is the Hierarchical Abstract Machines (HAM) framework introduced by Parr Russell (1998). Like our approach, HAMs begin with a representation of a high-level policy as an automaton (or a more general computer program; Andre & Russell, 2001; Marthi et al., 2004) and use reinforcement learn-ing to fill in low-level details. Because these approaches attempt to learn a single representation of the Q function for all subtasks and contexts, they require extremely strong formal assumptions about the form of the reward function and state representation (Andre & Russell, 2002) that the present work avoids by decoupling the policy representa-tion from the value function. They perform less effectively when applied to arbitrary state representations where these assumptions do not hold (Section 4.3). We are addition-ally unaware of past work showing that HAM automata can be automatically inferred for new tasks given a pre-trained model, while here we show that it is easy to solve the cor-responding problem for sketch followers (Section 4.5).

Our approach is also inspired by a number of recent efforts toward compositional reasoning and interaction with struc-tured deep models. Such models have been previously used for tasks involving question answering (Iyyer et al., 2014; Andreas et al., 2016) and relational reasoning (Socher et al., 2012), and more recently for multi-task, multi-robot trans-fer problems (Devin et al., 2016). In the present work—as in existing approaches employing dynamically assembled modular networks—task-specific training signals are prop-agated through a collection of composed discrete structures with tied weights. Here the composed structures spec-ify time-varying policies rather than feedforward computa-tions, and their parameters must be learned via interaction rather than direct supervision. Another closely related fam-ily of models includes neural programmers (Neelakantan et al., 2015) and programmer–interpreters (Reed & de Fre-itas, 2016), which generate discrete computational struc-tures but require supervision in the form of output actions or full execution traces.

We view the problem of learning from policy sketches as complementary to the instruction following problem stud-ied in the natural language processing literature. Existing work on instruction following focuses on mapping from natural language strings to symbolic action sequences that are then executed by a hard-coded interpreter (Branavan et al., 2009; Chen & Mooney, 2011; Artzi & Zettlemoyer, 2013; Tellex et al., 2011). Here, by contrast, we focus on learning to execute complex actions given symbolic repre-sentations as a starting point. Instruction following models may be viewed as joint policies over instructions and en-vironment observations (so their behavior is not defined in the absence of instructions), while the model described in this paper naturally supports adaptation to tasks where no sketches are available. We expect that future work might combine the two lines of research, bootstrapping policy learning directly from natural language hints rather than the semi-structured sketches used here.

Learning Modular Policies from Sketches

We consider a multitask reinforcement learning problem arising from a family of infinite-horizon discounted Markov decision processes in a shared environment. This environment is specified by a tuple $(S, A, P, \gamma )$, with $S$ a set of states, $A$ a set of low-level actions, $P : S \times A \times S \to R$ a transition probability distribution, and $\gamma$ a discount factor. Each task $t \in T$ is then specified by a pair $(R_t, \rho_t)$, with $R_t : S \to R$ a task-specific reward function and $\rho_t: S \to R$, an initial distribution over states. For a fixed sequence ${(s_i, a_i)}$ of states and actions obtained from a rollout of a given policy, we will denote the empirical return starting in state $s_i$ as $q_i = \sum_{j=i+1}^\infty \gamma^{j-i-1}R(s_j)$. In addition to the components of a standard multitask RL problem, we assume that tasks are annotated with sketches $K_t$ , each consisting of a sequence $(b_{t1},b_{t2},...)$ of high-level symbolic labels drawn from a fixed vocabulary $B$.

Model

We exploit the structural information provided by sketches by constructing for each symbol b a corresponding subpolicy $\pi_b$. By sharing each subpolicy across all tasks annotated with the corresponding symbol, our approach naturally learns the shared abstraction for the corresponding subtask, without requiring any information about the grounding of that task to be explicitly specified by annotation.

Pseudo Algorithms for Modular Multitask Reinforcement Learning with Policy Sketches

At each timestep, a subpolicy may select either a low-level action $a \in A$ or a special STOP action. We denote the augmented state space $A^+ := A \cup \{STOP\}$. At a high level, this framework is agnostic to the implementation of subpolicies: any function that takes a representation of the current state onto a distribution over $A^+$ will do.

In this paper, we focus on the case where each $\pi_b$ is represented as a neural network. These subpolicies may be viewed as options of the kind described by Sutton et al. (1999), with the key distinction that they have no initiation semantics, but are instead invokable everywhere, and have no explicit representation as a function from an initial state to a distribution over final states (instead implicitly using the STOP action to terminate).

Given a fixed sketch $(b_1, b_2,....)$, a task-specific policy $\Pi_r$ is formed by concatenating its associated subpolicies in sequence. In particular, the high-level policy maintains a sub-policy index i (initially 0), and executes actions from $\pi_{b_i}$ until the STOP symbol is emitted, at which point control is passed to bi+1 . We may thus think of as inducing a Markov chain over the state space $S \times B$, with transitions:

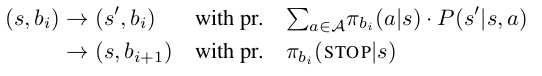
Note that is semi-Markov with respect to projection of the augmented state space $S \times B$ onto the underlying state space S. We denote the complete family of task-specific policies $\Pi := \bigcup_r \{ \Pi_r \}$, and let each $\pi_b$ be an arbitrary function of the current environment state parameterized by some weight vector $\theta_b$. The learning problem is to optimize over all $\theta_b$ to maximize expected discounted reward

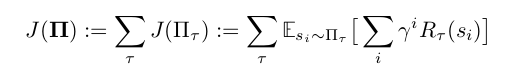
across all tasks $t \in T$.

Policy Optimization

Here that optimization is accomplished via a simple decoupled actor–critic method. In a standard policy gradient approach, with a single policy $\pi$ with parameters $\theta$, we compute gradient steps of the form (Williams, 1992):

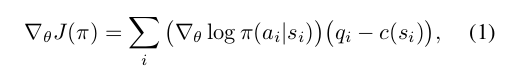
where the baseline or “critic” c can be chosen independently of the future without introducing bias into the gradient. Recalling our previous definition of $q_i$ as the empirical return starting from $s_i$, this form of the gradient corresponds to a generalized advantage estimator (Schulman et al., 2015a) with $\lambda = 1$. Here c achieves close to the optimal variance (Greensmith et al., 2004) when it is set exactly equal to the state-value function $V_{\pi} (s_i) = E_{\pi} q_i$ for the target policy $\pi$ starting in state $s_i$.

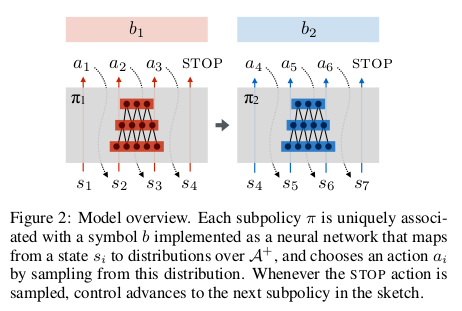
The situation becomes slightly more complicated when generalizing to modular policies built by sequencing sub-policies. In this case, we will have one subpolicy per symbol but one critic per task. This is because subpolicies $\pi_b$ might participate in a number of composed policies $\Pi_r$, each associated with its own reward function $R_r$ . Thus individual subpolicies are not uniquely identified with value functions, and the aforementioned subpolicy-specific state-value estimator is no longer well-defined. We extend the actor–critic method to incorporate the decoupling of policies from value functions by allowing the critic to vary per-sample (that is, per-task-and-timestep) depending on the reward function with which the sample is associated. Noting that

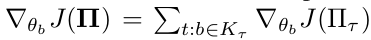
i.e. the sum of gradients of expected rewards across all tasks in which $\pi_b$ participates, we have:

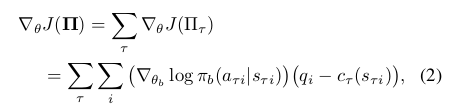
where each state-action pair $(s_{t_i}, a_{t_i})$ was selected by the subpolicy $\pi_b$ in the context of the task t.

Now minimization of the gradient variance requires that each $c_t$ actually depend on the task identity. (This follows immediately by applying the corresponding argument in Greensmith et al. (2004) individually to each term in the sum over t in Equation 2.) Because the value function is itself unknown, an approximation must be estimated from data. Here we allow these $c_t$ to be implemented with an arbitrary function approximator with parameters $\eta_t$ . This is trained to minimize a squared error criterion, with gradients given by

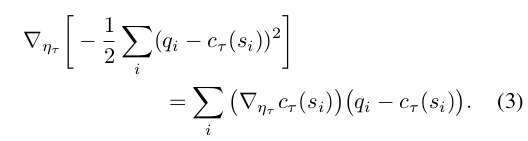
Alternative forms of the advantage estimator (e.g. the TD residual $R_t (s_i) + \gamma V_t(s_{i+1} - V_t(s_i))$ or any other member of the generalized advantage estimator family) can be easily substituted by simply maintaining one such estimator per task. Experiments (Section 4.4) show that conditioning on both the state and the task identity results in noticeable performance improvements, suggesting that the variance reduction provided by this objective is important for efficient joint learning of modular policies.

The complete procedure for computing a single gradient step is given in Algorithm 1. (The outer training loop over these steps, which is driven by a curriculum learning procedure, is specified in Algorithm 2.) This is an on-policy algorithm. In each step, the agent samples tasks from a task distribution provided by a curriculum (described in the following subsection). The current family of policies $\Pi$ is used to perform rollouts in each sampled task, accumulating the resulting tuples of (states, low-level actions, high-level symbols, rewards, and task identities) into a dataset $D$. Once $D$ reaches a maximum size D, it is used to compute gradients w.r.t. both policy and critic parameters, and the parameter vectors are updated accordingly. The step sizes $\alpha$ and $\beta$ in Algorithm 1 can be chosen adaptively using any first-order method.

Curriculum Learning

For complex tasks, like the one depicted in Figure 3b, it is difficult for the agent to discover any states with positive reward until many subpolicy behaviors have already been learned. It is thus a better use of the learner’s time to focus on “easy” tasks, where many rollouts will result in high reward from which appropriate subpolicy behavior can be inferred. But there is a fundamental tradeoff involved here: if the learner spends too much time on easy tasks before being made aware of the existence of harder ones, it may overfit and learn subpolicies that no longer generalize or exhibit the desired structural properties.

To avoid both of these problems, we use a curriculum learning scheme (Bengio et al., 2009) that allows the model to smoothly scale up from easy tasks to more difficult ones while avoiding overfitting. Initially the model is presented with tasks associated with short sketches. Once average reward on all these tasks reaches a certain threshold, the length limit is incremented. We assume that rewards across tasks are normalized with maximum achievable reward $0 < q_i < 1$ . Let $Er_t$ denote the empirical estimate of the expected reward for the current policy on task T. Then at each timestep, tasks are sampled in proportion $1-Er_t$, which by assumption must be positive.

Intuitively, the tasks that provide the strongest learning signal are those in which (1) the agent does not on average achieve reward close to the upper bound, but (2) many episodes result in high reward. The expected reward component of the curriculum addresses condition (1) by ensuring that time is not spent on nearly solved tasks, while the length bound component of the curriculum addresses condition (2) by ensuring that tasks are not attempted until high-reward episodes are likely to be encountered. Experiments show that both components of this curriculum learning scheme improve the rate at which the model converges to a good policy (Section 4.4).

The complete curriculum-based training procedure is specified in Algorithm 2. Initially, the maximum sketch length $l_{max}$ is set to 1, and the curriculum initialized to sample length-1 tasks uniformly. (Neither of the environments we consider in this paper feature any length-1 tasks; in this case, observe that Algorithm 2 will simply advance to length-2 tasks without any parameter updates.) For each setting of $l_{max}$, the algorithm uses the current collection of task policies to compute and apply the gradient step described in Algorithm 1. The rollouts obtained from the call to TRAIN-STEP can also be used to compute reward estimates $Er_t$ ; these estimates determine a new task distribution for the curriculum. The inner loop is repeated until the reward threshold $r_{good}$ is exceeded, at which point $l_{max}$ is incremented and the process repeated over a (now-expanded) collection of tasks.

Experiments

We evaluate the performance of our approach in three environments: a crafting environment, a maze navigation environment, and a cliff traversal environment. These environments involve various kinds of challenging low-level control: agents must learn to avoid obstacles, interact with various kinds of objects, and relate fine-grained joint activation to high-level locomotion goals. They also feature hierarchical structure: most rewards are provided only after the agent has completed two to five high-level actions in the appropriate sequence, without any intermediate goals to indicate progress towards completion.

Implementation

In all our experiments, we implement each subpolicy as a feedforward neural network with ReLU nonlinearities and a hidden layer with 128 hidden units, and each critic as a linear function of the current state. Each subpolicy network receives as input a set of features describing the current state of the environment, and outputs a distribution over actions. The agent acts at every timestep by sampling from this distribution. The gradient steps given in lines 8 and 9 of Algorithm 1 are implemented using RMSPROP (Tiele-man, 2012) with a step size of 0.001 and gradient clipping to a unit norm. We take the batch size D in Algorithm 1 to be 2000, and set $\gamma$= 0.9 in both environments. For curriculum learning, the improvement threshold $r_{good}$ is 0.8.

Conclusion & Critique

We have described an approach for multitask learning of deep multitask policies guided by symbolic policy sketches. By associating each symbol appearing in a sketch with a modular neural subpolicy, we have shown that it is possible to build agents that share behavior across tasks in order to achieve success in tasks with sparse and delayed rewards. This process induces an inventory of reusable and interpretable subpolicies which can be employed for zero-shot generalization when further sketches are available, and hierarchical reinforcement learning when they are not. Our work suggests that these sketches, which are easy to pro-duce and require no grounding in the environment, provide an effective scaffold for learning hierarchical policies from minimal supervision.