Don't Just Blame Over-parametrization: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 12: | Line 12: | ||
There are two activations used in the simulation: well-specified under-parametrized logistic regression as well as general convex ERM with the under-confident activation <math>\sigma_{underconf}</math>. The “calibration curves” were plotted for both activations: the x-axis is p, the y-axis is the average probability given the prediction. | There are two activations used in the simulation: well-specified under-parametrized logistic regression as well as general convex ERM with the under-confident activation <math>\sigma_{underconf}</math>. The “calibration curves” were plotted for both activations: the x-axis is p, the y-axis is the average probability given the prediction. | ||
[[File:simulation.png]] | [[File:simulation.png|700px|thumb|center]] | ||
The figure show four main results: First, the logistic regression is over-confident at all <math>\kappa</math>. Second, over-confidence is more severe when <math>\kappa</math> increases, suggests the conclusion of the theory holds more broadly than its assumptions. Third, <math>\sigma_{underconf}</math> leads to under-confidence for <math>p \in (0.5, 0.51)</math>, which verifies Theorem 2 and Corollary 3. Finally, theoretical prediction closely matches the simulation, further confirms our theory. | The figure show four main results: First, the logistic regression is over-confident at all <math>\kappa</math>. Second, over-confidence is more severe when <math>\kappa</math> increases, suggests the conclusion of the theory holds more broadly than its assumptions. Third, <math>\sigma_{underconf}</math> leads to under-confidence for <math>p \in (0.5, 0.51)</math>, which verifies Theorem 2 and Corollary 3. Finally, theoretical prediction closely matches the simulation, further confirms our theory. | ||
| Line 18: | Line 18: | ||
The generality of our theory beyond the Gaussian input assumption and the binary classification setting was further tested using dataset CIFAR10 by running multi-class logistic regression on the first five classes on it. The author performed logistic regression on two kinds of labels: true label and pseudo-label generated from the multi-class logistic (softmax) model. | The generality of our theory beyond the Gaussian input assumption and the binary classification setting was further tested using dataset CIFAR10 by running multi-class logistic regression on the first five classes on it. The author performed logistic regression on two kinds of labels: true label and pseudo-label generated from the multi-class logistic (softmax) model. | ||
[[File:DJB_CIFAR10.png]] | [[File:DJB_CIFAR10.png|700px|thumb|center]] | ||
The figure show that the logistic regression is over-confident on both labels, where the over-confidence is more severe on the pseudo-labels than the true labels. This suggests the result that logistic regression is inherently over-confident may hold more broadly for other under-parametrized problems without strong assumptions on the input distribution, or even when the labels are not necessarily realizable by the model. | The figure show that the logistic regression is over-confident on both labels, where the over-confidence is more severe on the pseudo-labels than the true labels. This suggests the result that logistic regression is inherently over-confident may hold more broadly for other under-parametrized problems without strong assumptions on the input distribution, or even when the labels are not necessarily realizable by the model. | ||
Revision as of 23:28, 11 November 2021
Presented by
Jared Feng, Xipeng Huang, Mingwei Xu, Tingzhou Yu
Introduction
..........
Experiments
The authors conducted two experiments to test our theories: the first was based on simulation, and the second used the data CIFAR10.
There are two activations used in the simulation: well-specified under-parametrized logistic regression as well as general convex ERM with the under-confident activation [math]\displaystyle{ \sigma_{underconf} }[/math]. The “calibration curves” were plotted for both activations: the x-axis is p, the y-axis is the average probability given the prediction.
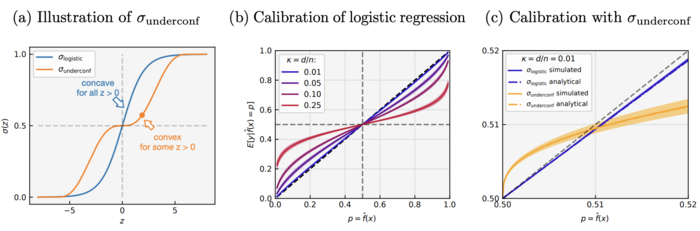
The figure show four main results: First, the logistic regression is over-confident at all [math]\displaystyle{ \kappa }[/math]. Second, over-confidence is more severe when [math]\displaystyle{ \kappa }[/math] increases, suggests the conclusion of the theory holds more broadly than its assumptions. Third, [math]\displaystyle{ \sigma_{underconf} }[/math] leads to under-confidence for [math]\displaystyle{ p \in (0.5, 0.51) }[/math], which verifies Theorem 2 and Corollary 3. Finally, theoretical prediction closely matches the simulation, further confirms our theory.
The generality of our theory beyond the Gaussian input assumption and the binary classification setting was further tested using dataset CIFAR10 by running multi-class logistic regression on the first five classes on it. The author performed logistic regression on two kinds of labels: true label and pseudo-label generated from the multi-class logistic (softmax) model.
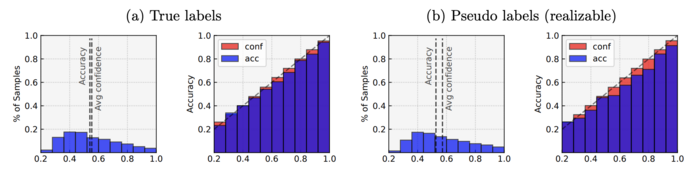
The figure show that the logistic regression is over-confident on both labels, where the over-confidence is more severe on the pseudo-labels than the true labels. This suggests the result that logistic regression is inherently over-confident may hold more broadly for other under-parametrized problems without strong assumptions on the input distribution, or even when the labels are not necessarily realizable by the model.