Time-series Generative Adversarial Networks: Difference between revisions
(Created page with "== Presented By == Govind Sharma (20817244) == Introduction == A time-series model should not only be good at learning the overall distribution of temporal features within d...") |
|||
| Line 4: | Line 4: | ||
== Introduction == | == Introduction == | ||
A time-series model should not only be good at learning the overall distribution of temporal features within different time points, but it should also be good at capturing the dynamic relationship between the temporal variables across time. | A time-series model should not only be good at learning the overall distribution of temporal features within different time points, but it should also be good at capturing the dynamic relationship between the temporal variables across time. | ||
The popular autoregressive approach in time-series or sequence analysis is generally focused on minimizing the error involved in multi-step sampling improving the temporal dynamics of data. In this approach, the distribution of sequences is broken down into a product of conditional probabilities. The deterministic nature of this approach works well for forecasting but it is not very promising in a generative setup. The GAN approach when applied on time-series directly simply tries to learn p(X|t) using generator and discriminator setup but this fails to leverage the prior probabilities like in the case of the autoregressive case. | |||
This paper proposes a novel GAN architecture that combines the two approaches (unsupervised GANs and supervised autoregressive) that allow a generative model to have the ability to preserve temporal dynamics along with learning the overall distribution. This mechanism has been termed as Time-series Generative Adversarial Network or TimeGAN. To incorporate supervised learning of data into the GAN architecture, this approach makes use of an embedding network that provides a reversible mapping between the temporal features and their latent representations. The key insight of this paper is that the embedding network is trained in parallel with the generator/discriminator network. | The popular autoregressive approach in time-series or sequence analysis is generally focused on minimizing the error involved in multi-step sampling improving the temporal dynamics of data. In this approach, the distribution of sequences is broken down into a product of conditional probabilities. The deterministic nature of this approach works well for forecasting but it is not very promising in a generative setup. The GAN approach when applied on time-series directly simply tries to learn <math>p(X|t)</math> using generator and discriminator setup but this fails to leverage the prior probabilities like in the case of the autoregressive case. | ||
This paper proposes a novel GAN architecture that combines the two approaches (unsupervised GANs and supervised autoregressive) that allow a generative model to have the ability to preserve temporal dynamics along with learning the overall distribution. This mechanism has been termed as '''Time-series Generative Adversarial Network''' or '''TimeGAN'''. To incorporate supervised learning of data into the GAN architecture, this approach makes use of an embedding network that provides a reversible mapping between the temporal features and their latent representations. The key insight of this paper is that the embedding network is trained in parallel with the generator/discriminator network. | |||
This approach leverages the flexibility of GANs together with the control of the autoregressive model resulting in significant improvements in the generation of realistic time-series. | This approach leverages the flexibility of GANs together with the control of the autoregressive model resulting in significant improvements in the generation of realistic time-series. | ||
== Related Work == | |||
The TimeGAN mechanism combines ideas from different research threads in time-series analysis. | |||
Due to differences between closed-loop training (ground truth conditioned) and open-loop inference (previous guess conditioned), there can be significant prediction error in multi-step sampling in autoregressive recurrent networks. Different methods have been proposed to remedy this including Scheduled Sampling where models are trained to output based on a combination of ground truth and previous outputs, training and auxiliary discriminator that helps separate free-running and teacher-forced hidden states accelerating convergence and Actor-critic methods that condition on target outputs estimating the next-token value that nudges the actor’s free-running predictions. While all these proposed methods try to improve step-sampling, they are still inherently deterministic. | |||
Direct application of GAN architecture on time-series data like C-RNN-GAN or RCGAN try to generate the time-series data recurrently sometimes taking the generated output from the previous step as input (like in case of RCGAN) along with the noise vector. Recently, adding time stamp information for conditioning has also been proposed in these setups to handle inconsistent sampling. But these approaches remain very GAN-centric and depend only on the traditional adversarial feedback (fake/real) to learn which is not sufficient to capture the temporal dynamics. | |||
== Problem Formulation == | |||
Generally, time-series data can be decomposed into two components: static features (variables that remain the same over long or entire stretches of time) and temporal features (variables that change frequently with time steps). The paper uses <math>S</math> to denote the static component and <math>X</math> to denote the temporal features. Using this setting, input to the model can be thought of as a tuple of <math>(S, X_{1:t})</math> that has a joint distribution say <math>p</math>. The objective of a generative model is of course to learn from training data, an approximation of the original distribution <math>p(S, X)</math> i.e. <math>\hat{p}(S, X)</math>. Along with this joint distribution, another objective is to simultaneously learn the autoregressive decomposition of <math>p(S, X_{1:T}) = p(S)\prod_tp(X_t|S, X_{1:t-1})</math> as well. This gives the following two objective functions. | |||
<div align="center"><math>min_\hat{p}D\left(p(S, X_{1:T})||\hat{p}(S, X_{1:T})\right)</math>, and </div> | |||
<div align="center"><math>min_\hat{p}D\left(p(X_t | S, X_{1:t-1})||\hat{p}(X_t | S, X_{1:t-1})\right)</math></div> | |||
== Proposed Architecture == | |||
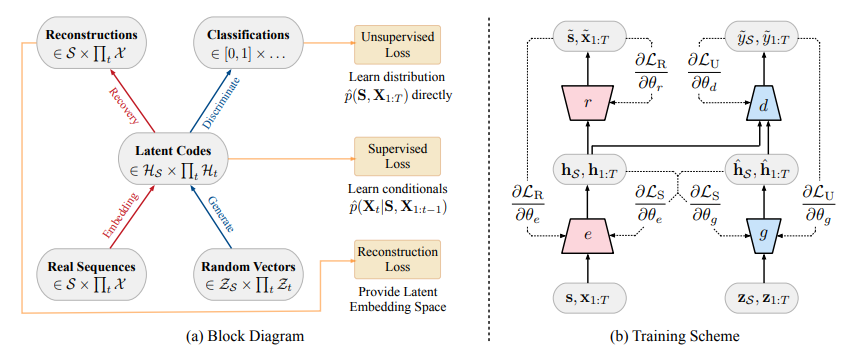
Apart from the normal GAN components of sequence generator and sequence discriminator, TimeGAN has two additional elements: an embedding function and a recovery function. As mentioned before, all these components are trained concurrently. Figure 1 shows how these four components are arranged and how does information flows between them during training in TimeGAN. | |||
<div align="center"> [[File:Architecture_TimeGAN.PNG|Architecture of TimeGAN.]] </div> | |||
<div align="center">'''Figure 1'''</div> | |||
Revision as of 22:18, 1 December 2020
Presented By
Govind Sharma (20817244)
Introduction
A time-series model should not only be good at learning the overall distribution of temporal features within different time points, but it should also be good at capturing the dynamic relationship between the temporal variables across time.
The popular autoregressive approach in time-series or sequence analysis is generally focused on minimizing the error involved in multi-step sampling improving the temporal dynamics of data. In this approach, the distribution of sequences is broken down into a product of conditional probabilities. The deterministic nature of this approach works well for forecasting but it is not very promising in a generative setup. The GAN approach when applied on time-series directly simply tries to learn [math]\displaystyle{ p(X|t) }[/math] using generator and discriminator setup but this fails to leverage the prior probabilities like in the case of the autoregressive case.
This paper proposes a novel GAN architecture that combines the two approaches (unsupervised GANs and supervised autoregressive) that allow a generative model to have the ability to preserve temporal dynamics along with learning the overall distribution. This mechanism has been termed as Time-series Generative Adversarial Network or TimeGAN. To incorporate supervised learning of data into the GAN architecture, this approach makes use of an embedding network that provides a reversible mapping between the temporal features and their latent representations. The key insight of this paper is that the embedding network is trained in parallel with the generator/discriminator network.
This approach leverages the flexibility of GANs together with the control of the autoregressive model resulting in significant improvements in the generation of realistic time-series.
Related Work
The TimeGAN mechanism combines ideas from different research threads in time-series analysis.
Due to differences between closed-loop training (ground truth conditioned) and open-loop inference (previous guess conditioned), there can be significant prediction error in multi-step sampling in autoregressive recurrent networks. Different methods have been proposed to remedy this including Scheduled Sampling where models are trained to output based on a combination of ground truth and previous outputs, training and auxiliary discriminator that helps separate free-running and teacher-forced hidden states accelerating convergence and Actor-critic methods that condition on target outputs estimating the next-token value that nudges the actor’s free-running predictions. While all these proposed methods try to improve step-sampling, they are still inherently deterministic.
Direct application of GAN architecture on time-series data like C-RNN-GAN or RCGAN try to generate the time-series data recurrently sometimes taking the generated output from the previous step as input (like in case of RCGAN) along with the noise vector. Recently, adding time stamp information for conditioning has also been proposed in these setups to handle inconsistent sampling. But these approaches remain very GAN-centric and depend only on the traditional adversarial feedback (fake/real) to learn which is not sufficient to capture the temporal dynamics.
Problem Formulation
Generally, time-series data can be decomposed into two components: static features (variables that remain the same over long or entire stretches of time) and temporal features (variables that change frequently with time steps). The paper uses [math]\displaystyle{ S }[/math] to denote the static component and [math]\displaystyle{ X }[/math] to denote the temporal features. Using this setting, input to the model can be thought of as a tuple of [math]\displaystyle{ (S, X_{1:t}) }[/math] that has a joint distribution say [math]\displaystyle{ p }[/math]. The objective of a generative model is of course to learn from training data, an approximation of the original distribution [math]\displaystyle{ p(S, X) }[/math] i.e. [math]\displaystyle{ \hat{p}(S, X) }[/math]. Along with this joint distribution, another objective is to simultaneously learn the autoregressive decomposition of [math]\displaystyle{ p(S, X_{1:T}) = p(S)\prod_tp(X_t|S, X_{1:t-1}) }[/math] as well. This gives the following two objective functions.
Proposed Architecture
Apart from the normal GAN components of sequence generator and sequence discriminator, TimeGAN has two additional elements: an embedding function and a recovery function. As mentioned before, all these components are trained concurrently. Figure 1 shows how these four components are arranged and how does information flows between them during training in TimeGAN.