Influenza Forecasting Framework based on Gaussian Processes

Abstract

This paper presents a novel framework for seasonal epidemic forecasting using Gaussian process regression. Resulting retrospective forecasts, trained on a subset of the publicly available CDC influenza-like-illness (ILI) data-set, outperformed four state-of-the-art models when compared using the official CDC scoring rule (log-score).

Background

Each year, the seasonal influenza epidemic affects public health at a massive scale, resulting in 38 million cases, 400 000 hospitalizations, and 22 000 deaths in the United States in 2019-2020 alone [1]. Given this, reliable forecasts of future influenza development are invaluable, because they allow for improved public health policies and informed resource development and allocation. Many statistical methods have been developed to use data from the CDC and other real-time data sources, such as Google Trends to forecast influenza activities.

Given the process of data collection and surveillance lag, accurate statistics for influenza warning systems are often delayed by some margin of time, making early prediction imperative. However, there are challenges in long-term epidemic forecasting. First, the temporal dependency is hard to capture with short-term input data. Without manually added seasonal trends, most statistical models fail to provide high accuracy. Second, the influence from other locations has not been exhaustively explored with limited data input. Spatio-temporal effects would therefore require adequate data sources to achieve good performance.

Related Work

Given the value of epidemic forecasts, the CDC regularly publishes ILI data and has funded a seasonal ILI forecasting challenge. This challenge has to lead to four states of the art models in the field; MSS, a physical susceptible-infected-recovered model with assumed linear noise [4]; SARIMA, a framework based on seasonal auto-regressive moving average models [2]; and LinEns, an ensemble of three linear regression models.

Motivation

It has been shown that LinEns forecasts outperform the other frameworks on the ILI data-set. However, this framework assumes a deterministic relationship between the epidemic week and its case count, which does not reflect the stochastic nature of the trend. Therefore, it is natural to ask whether a similar framework that assumes a stochastic relationship between these variables would provide better performance. This motivated the development of the proposed Gaussian process regression framework and the subsequent performance comparison to the benchmark models.

Gaussian Process Regression

A Gaussian process is specified with a mean function and a kernel function. Besides, the mean and the variance function of the Gaussian process is defined by: \[\mu(x) = k(x, X)^T(K_n+\sigma^2I)^{-1}Y\] \[\sigma(x) = k^{**}(x,x)-k(x,X)^T(K_n+\sigma^2I)^{-1}k(x,X)\] where \(K_n\) is the covariance matrix and for the kernel, it is being specified that it will use the Gaussian kernel.

Consider the following set up: let [math]\displaystyle{ X = [\mathbf{x}_1,\ldots,\mathbf{x}_n] }[/math] [math]\displaystyle{ (d\times n) }[/math] be your training data, [math]\displaystyle{ \mathbf{y} = [y_1,y_2,\ldots,y_n]^T }[/math] be your noisy observations where [math]\displaystyle{ y_i = f(\mathbf{x}_i) + \epsilon_i }[/math], [math]\displaystyle{ (\epsilon_i:i = 1,\ldots,n) }[/math] i.i.d. [math]\displaystyle{ \sim \mathcal{N}(0,{\sigma}^2) }[/math], and [math]\displaystyle{ f }[/math] is the trend we are trying to model (by [math]\displaystyle{ \hat{f} }[/math]). Let [math]\displaystyle{ \mathbf{x}^* }[/math] [math]\displaystyle{ (d\times 1) }[/math] be your test data point, and [math]\displaystyle{ \hat{y} = \hat{f}(\mathbf{x}^*) }[/math] be your predicted outcome.

Instead of assuming a deterministic form of [math]\displaystyle{ f }[/math], and thus of [math]\displaystyle{ \mathbf{y} }[/math] and [math]\displaystyle{ \hat{y} }[/math] (as classical linear regression would, for example), Gaussian process regression assumes [math]\displaystyle{ f }[/math] is stochastic. More precisely, [math]\displaystyle{ \mathbf{y} }[/math] and [math]\displaystyle{ \hat{y} }[/math] are assumed to have a joint prior distribution. Indeed, we have

$$ (\mathbf{y},\hat{y}) \sim \mathcal{N}(0,\Sigma(X,\mathbf{x}^*)) $$

where [math]\displaystyle{ \Sigma(X,\mathbf{x}^*) }[/math] is a matrix of covariances dependent on some kernel function [math]\displaystyle{ k }[/math]. In this paper, the kernel function is assumed to be Gaussian and takes the form

$$ k(\mathbf{x}_i,\mathbf{x}_j) = \sigma^2\exp(-\frac{1}{2}(\mathbf{x}_i-\mathbf{x}^j)^T\Sigma(\mathbf{x}_i-\mathbf{x}_j)). $$

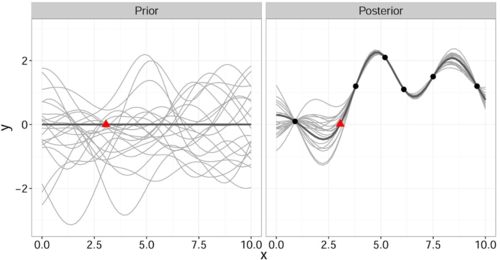
It is important to note that this gives a joint prior distribution of functions (Fig. 1 left, grey curves).

By restricting this distribution to contain only those functions (Fig. 1 right, grey curves) that agree with the observed data points [math]\displaystyle{ \mathbf{x} }[/math] (Fig. 1 right, solid black) we obtain the posterior distribution for [math]\displaystyle{ \hat{y} }[/math] which has the form

$$ p(\hat{y} | \mathbf{x}^*, X, \mathbf{y}) \sim \mathcal{N}(\mu(\mathbf{x}^*,X,\mathbf{y}),\sigma(\mathbf{x}^*,X)) $$

Figure 1. Gaussian process regression: Select the functions from your joint prior distribution (left, grey curves) with mean [math]\displaystyle{ 0 }[/math] (left, bold line) that agree with the observed data points (right, black bullets). These form your posterior distribution (right, grey curves) with mean [math]\displaystyle{ \mu(\mathbf{x}) }[/math] (right, bold line). Red triangle helps compare the two images (location marker) [3].

Data-set

Let [math]\displaystyle{ d_j^i }[/math] denote the number of epidemic cases recorded in week [math]\displaystyle{ j }[/math] of season [math]\displaystyle{ i }[/math], and let [math]\displaystyle{ j^* }[/math] and [math]\displaystyle{ i^* }[/math] denote the current week and season, respectively. The ILI data-set contains [math]\displaystyle{ d_j^i }[/math] for all previous weeks and seasons, up to the current season with a 1-3 week publishing delay. Note that a season refers to the time of year when the epidemic is prevalent (e.g. an influenza season lasts 30 weeks and contains the last 10 weeks of year k, and the first 20 weeks of year k+1). The goal is to predict [math]\displaystyle{ \hat{y}_T = \hat{f}_T(x^*) = d^{i^*}_{j* + T} }[/math] where [math]\displaystyle{ T, \;(T = 1,\ldots,K) }[/math] is the target week (how many weeks into the future that you want to predict).

To do this, a design matrix [math]\displaystyle{ X }[/math] is constructed where each element [math]\displaystyle{ X_{ji} = d_j^i }[/math] corresponds to the number of cases in week (row) j of season (column) i. The training outcomes [math]\displaystyle{ y_{i,T}, i = 1,\ldots,n }[/math] correspond to the number of cases that were observed in target week [math]\displaystyle{ T,\; (T = 1,\ldots,K) }[/math] of season [math]\displaystyle{ i, (i = 1,\ldots,n) }[/math].

Proposed Framework

To compute [math]\displaystyle{ \hat{y} }[/math], the following algorithm is executed.

1. Let [math]\displaystyle{ J \subseteq \{j^*-4 \leq j \leq j^*\} }[/math] (subset of possible weeks).
2. Assemble the Training Set [math]\displaystyle{ \{X_J, \mathbf{y}_{T,J}\} }[/math]
3. Train the Gaussian process
4. Calculate the distribution of [math]\displaystyle{ \hat{y}_{T,J} }[/math] using [math]\displaystyle{ p(\hat{y}_{T,J} | \mathbf{x}^*, X_J, \mathbf{y}_{T,J}) \sim \mathcal{N}(\mu(\mathbf{x}^*,X,\mathbf{y}_{T,J}),\sigma(\mathbf{x}^*,X_J)) }[/math]
5. Set [math]\displaystyle{ \hat{y}_{T,J} =\mu(x^*,X_J,\mathbf{y}_{T,J}) }[/math]
6. Repeat steps 2-5 for all sets of weeks [math]\displaystyle{ J }[/math]
7. Determine the best 3 performing sets J (on the 2010/11 and 2011/12 validation sets)
8. Calculate the ensemble forecast by averaging the 3 best performing predictive distribution densities i.e. [math]\displaystyle{ \hat{y}_T = \frac{1}{3}\sum_{k=1}^3 \hat{y}_{T,J_{best}} }[/math]

Results

To demonstrate the accuracy of their results, retrospective forecasting was done on the ILI data-set. In other words, the Gaussian process model was trained to assume a previous season (2012/13) was the current season. In this fashion, the forecast could be compared to the already observed true outcome.

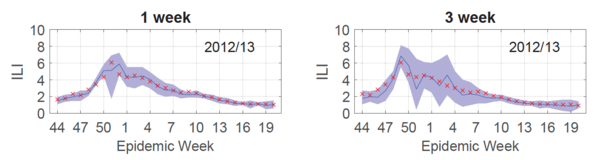
To produce a forecast for the entire 2012/13 season, 30 Gaussian processes were trained (each influenza season has 30 test points [math]\displaystyle{ \mathbf{x^*} }[/math]) and a curve connecting the predicted outputs [math]\displaystyle{ y_T = \hat{f}(\mathbf{x^*)} }[/math] was plotted (Fig.2, blue line). As shown in Fig.2, this forecast (blue line) was reliable for both 1 (left) and 3 (right) week targets, given that the 95% prediction interval (Fig.2, purple shaded) contained the true values (Fig.2, red x's) 95% of the time.

Figure 2. Retrospective forecasts and their uncertainty: One week retrospective influenza forecasting for two targets (T = 1, 3). Red x’s are the true observed values, and blue lines and purple shaded areas represent point forecasts and 95% prediction intervals, respectively.

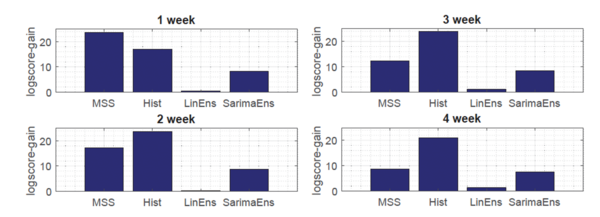
Moreover, as shown in Fig.3, the novel Gaussian process regression framework outperformed all state-of-the-art models, included LinEns, for four different targets [math]\displaystyle{ (T = 1,\ldots, 4) }[/math], when compared using the official CDC scoring criterion log-score. Log-score describes the logarithmic probability of the forecast being within an interval around the true value.

Figure 3. Average log-score gain of proposed framework: Each bar shows the mean seasonal log-score gain of the proposed framework vs. the given state-of-the-art model, and each panel corresponds to a different target week [math]\displaystyle{ T = 1,...4 }[/math].

Conclusion

This paper presented a novel framework for forecasting seasonal epidemics using Gaussian process regression that outperformed multiple state-of-the-art forecasting methods on the CDC's ILI data-set. Hence, this work may play a key role in future influenza forecasting and as result, the improvement of public health policies and resource allocation.

Critique

The proposed framework provides a computationally efficient method to forecast any seasonal epidemic count data that is easily extendable to multiple target types. In particular; one can compute key parameters such as the peak infection incidence ([math]\displaystyle{ \hat{y} = max_{0 \leq j \leq 52} d^i_j }[/math]), the timing of the peak infection incidence ([math]\displaystyle{ \hat{y} = argmax_{0 \leq j \leq 52} d^i_j }[/math]) and the final epidemic size of a season ([math]\displaystyle{ \hat{y} = \sum_{j=1}^{52} d^i_j }[/math]). However, given it is not a physical model, it cannot provide insights on parameters describing the disease spread. Moreover, the framework requires training data and hence, is not applicable for non-seasonal epidemics.

This paper provides a state of the art approach for forecasting epidemics. It would have been interesting to see other types of kernels being used, such as a periodic kernel ([math]\displaystyle{ k(x, x') = \sigma^2 \exp{-\frac{2 \sin^2 (\pi|x-x'|/p}{l^2}} }[/math]), as intuitively epidemics are known to have waves within seasons. This may have resulted in better-calibrated uncertainty estimates as well.

It is mentioned that the the framework might not be good for non-seasonal epidemics because it requires training data, given that the COVID-19 pandemic comes in multiple waves and we have enough data from the first wave and second wave, we might be able to use this framework to predict the third wave and possibly the fourth one as well. It'd be interesting to see this forecasting framework being trained using the data from the first and second wave of COVID-19.

References

[1] Estimated Influenza Illnesses, Medical visits, Hospitalizations, and Deaths in the United States - 2019–2020 Influenza Season. (2020). Retrieved November 16, 2020, from https://www.cdc.gov/flu/about/burden/2019-2020.html

[2] Ray, E. L., Sakrejda, K., Lauer, S. A., Johansson, M. A.,and Reich, N. G. (2017).Infectious disease prediction with kernel conditional densityestimation.Statistics in Medicine, 36(30):4908–4929.

[3] Schulz, E., Speekenbrink, M., and Krause, A. (2017).A tutorial on gaussian process regression with a focus onexploration-exploitation scenarios.bioRxiv.

[4] Zimmer, C., Leuba, S. I., Cohen, T., and Yaesoubi, R.(2019).Accurate quantification of uncertainty in epidemicparameter estimates and predictions using stochasticcompartmental models.Statistical Methods in Medical Research,28(12):3591–3608.PMID: 30428780.