what game are we playing

Authors

Yuxin Wang, Evan Peters, Yifan Mou, Sangeeth Kalaichanthiran

Quantal response in Normal form games

The game-solving module provides all elements required in differentiable learning, which maps contextual features to payoff matrices and computes equilibrium strategies under a set of contextual features. This paper will learn zero-sum games, which considers a wide class of adversarial environments, and it starts with normal form games since they have game solver and learning approach capturing much of intuition and basic methodology.

In two-player zero-sum games with payoff matrix P, and strategies u and v employed by min and max player respectively, we introduce a classic min-max formulation: $$ \min_x \max_y \ u^T P v \ (1) \\ subject\ to\ 1^T u =1, u \ge 0 \ (2) \\ 1^T v =1, v \ge 0, \ (3) \\ $$ The solution [math]\displaystyle{ (u^*, v_0) }[/math] to this optimization and the solution [math]\displaystyle{ (u_0,v^*) }[/math] of the corresponding problem with inverse player order forms the Nash equilibrium. Here we consider the case where the payoff matrix P is not known. To recover the true underlying payoff matrix P or a function form P(x) depending on the current context, we observe samples of actions [math]\displaystyle{ a^{(i)}, i =1,...,N }[/math] from one or both players, sampled from the equilibrium strategies [math]\displaystyle{ (u^*,v^*) }[/math].

However, NE is poorly suited because NEs are overly strict and discontinuous with respect to P, and NEs may not be unique. Thus, modelling the player's action with the quantal response equilibria is proposed to address these issues. Specifically, we consider the logit equilibrium where the noise follows a Gumbel distribution. For zero-sum games, the logit equilibrium obeys the fixed point: $$ u^* _i = \frac {exp(Pv)_i}{\sum_{q \in [n]} exp (-Pv)_q}, \ v^* _j= \frac {exp(P^T u)_j}{\sum_{q \in [m]} exp (P^T u)_q} .\ (4) $$ For a fixed opponent strategy, the logit equilibrium corresponding to a strategy is regularized by Gibbs entropy [Mertikopoulos and Sandholm, 2016], which is strictly convex. Thus, the regularized best response is unique.

Then to integrate zero-sum solver into an end-to-end learning, we introduce a method involving both a particular approach to solving the QRE and to differentiating through its solution.

QRE solver: To find the fixed point in (4), it is equivalent to solve the regularized min-max game $$ (5) \ \min_{u \in \mathbb{R}^n} \max_{v \in \mathbb{R}^m} \ u^T P v -H(v) + H(u) \\ subject\ to\ 1^T u =1, \ 1^T v =1, $$ where H(y) is the Gibbs entropy [math]\displaystyle{ \sum_i y_i log y_i }[/math]. Entropy regularization guarantees the non-negative condition and makes the equilibrium continuous with respect to P, which means players are encouraged to play more randomly and all actions have non-zero probability. Moreover, this problem has a unique saddle point corresponding to [math]\displaystyle{ (u^*, v^*) }[/math].

Using a primal-dual Newton Method to solve the QRE for two-player zero-sum games, we firstly find KKT conditions for the problem: $$ (6) Pv + log(u) + 1 +\mu 1 = 0 \\ P^T v -log(v) -1 +\nu 1 = 0 \\ 1^T u = 1, \ 1^T v = 1, $$ where [math]\displaystyle{ (\mu, \ \nu) }[/math] are Lagrange multipliers for the equality constraints on u, v respectively. Then by Newton's method, we get the update rule: $$ Q \begin{bmatrix} \Delta u \\ \Delta v \\ \Delta \mu \\ \Delta \nu \\ \end{bmatrix} = - \begin{bmatrix} P v + logu + 1 + \mu 1 \\ P^T u - log v - 1 + \nu 1 \\ 1^T u - 1 \\ 1^T v - 1 \\ \end{bmatrix} $$

Learning Extensive form games

The normal form representation for games where players have many choices quickly becomes intractable. For example, consider a chess game: One the first turn, player 1 has 20 possible moves and then player 2 has 20 possible responses. If in the following number of turns each player is estimated to have ~30 possible moves and if a typical game is 40 moves per player, the total number of strategies is roughly [math]\displaystyle{ 10^{120} }[/math] per player (this is known as the Shannon number for game-tree complexity of chess) and so the payoff matrix for a typical game of chess must therefore have [math]\displaystyle{ O(10^{240}) }[/math] entries.

Instead, it is much more useful to represent the game graphically (in "Extensive form"). We'll also need to consider types of games where there is incomplete information - players do not necessarily have access to the full state of the game. An example of this is one-card poker: (1) Each player draws a single card from a 13-card deck (ignore suits) (2) Player 1 decides whether to bet/hold (3) Player 2 decides whether to call/raise (4) Player 1 must either call/fold if Player 2 raised. From this description, player 1 has [math]\displaystyle{ 2^{13} }[/math] possible first moves (all combinations of (card, raise/hold)) and has [math]\displaystyle{ 2^{13} }[/math] possible second moves (whenever player 1 gets a second move) for a total of [math]\displaystyle{ 2^{26} }[/math] possible strategies. In addition, Player 1 never knows what cards player 2 has and vice versa. So instead of representing the game with a huge payoff matrix we can instead represent it as a simple decision tree (for a single drawn card of player 1):

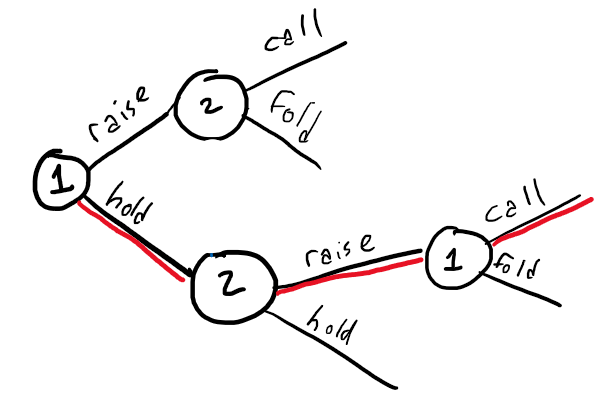
where player 1 is represented by "1", a node that has two branches corresponding to the allowed moves of player 1. However there must also be a notion of information available to either player: While this tree might correspond to say, player 1 holding a "9", it contains no information on what card player 2 is holding. This leads to the definition of an information set: the set of all nodes belonging to a single player for which the other player cannot distinguish which node has been reached. The information set may therefore be treated as a node itself, for which actions stemming from the node must be chosen in ignorance to what the other player did immediately before arriving at the node. In the poker example, the full game tree consists of 13 repetitions of the tree shown above and an example of an information set for player 1 is the set of all of nodes owned by player 2 that immediately follow player 1's decision to hold. In other words, if player 1 holds there are 13 possible nodes describing the responses of player 2 (raise/hold for player 2 having card = ace, 1, ... King) and all 13 of these nodes are indistinguishable to player 1, and so form an information set for player 1.

The following is a review of important concepts for extensive form games first formalized in [2]. Let [math]\displaystyle{ \mathcal{I}_i }[/math] be the set of all information sets for player i, and for each [math]\displaystyle{ t \in \mathcal{I}_i }[/math] let [math]\displaystyle{ \sigma_t }[/math] be the actions taken by player i to arrive at [math]\displaystyle{ t }[/math] and [math]\displaystyle{ C_t }[/math] be the actions that player i can take from [math]\displaystyle{ u }[/math]. Then the set of all possible sequences that can be taken by player i is given by

$$ S_i = \{\emptyset \} \cup \{ \sigma_t c | u\in \mathcal{I}_i, c \in C_t \} $$

So for the one-card poker we would have [math]\displaystyle{ S_1 = \{\emptyset, \text{raise}, \text{hold}, \text{hold-call}, \text{hold-fold\} } }[/math]. From the possible sequences follows two important concepts:

1. The EFG payoff matrix [math]\displaystyle{ P }[/math] is size [math]\displaystyle{ |S_1| \times |S_2| }[/math] (this is all possible actions available to either player), is populated with rewards from each leaf of the tree (or "zero" for each [math]\displaystyle{ (s_1, s_2) }[/math] that is an invalid pair), and the expected payoff for realization plans [math]\displaystyle{ (u, v) }[/math] is given by [math]\displaystyle{ u^T P v }[/math]
2. A realization plan [math]\displaystyle{ u \in \mathbb{R}^{|S_1|} }[/math] for player 1 ([math]\displaystyle{ v \in \mathbb{R}^{|S_2|} }[/math] for player 2 ) will describe probabilities for players to carry out each possible sequence, and each realization plan must be constrained by (i) compatibility of sequences (e.g. "raise" is not compatible with "hold-call") and (ii) information sets available to the player. These constraints are linear: $$ Eu = e \\ Fv = f $$ where [math]\displaystyle{ e = f = (1, 0, ..., 0)^T }[/math] and [math]\displaystyle{ E, F }[/math] contain entries in [math]\displaystyle{ {-1, 0, 1} }[/math] describing compatibility and information sets.

The paper's main contribution is to develop a minmax problem for extensive form games:

$$ \min_u \max_v u^T P v + \sum_{t\in \mathcal{I}_1} \sum_{c \in C_t} u_c \log \frac{u_c}{u_{p_t}} - \sum_{t\in \mathcal{I}_2} \sum_{c \in C_t} v_c \log \frac{v_c}{v_{p_t}} $$

where [math]\displaystyle{ p_t }[/math] is the action immediately preceding information set [math]\displaystyle{ t }[/math]. Intuitively, each sum resembles a cross entropy over the distribution of probabilities in the realization plan comparing each probability to proceed from an information set to the probability to arrive at that information set. Importantly, these entropies are strictly convex or concave (for player 1 and player 2 respectively) [3] so that the minmax problem will have a unique solution and the objective function is continuous and continuously differntiable - this means there is a way to optimize the function. As noted in Theorem 1 of [1], the solution to this problem is equivalently a solution for the QRE of the game in reduced normal form.

Having decided on a cost function, the method of Lagrange multipliers my be used to construct the Lagrangian that encodes the known constraints ([math]\displaystyle{ Eu = e \,, Fv = f }[/math], and [math]\displaystyle{ u, v \geq 0 }[/math]), and then optimize the Lagrangian using Newton's method. Accounting for the constraints, the Lagrangian becomes

$$ \mathcal{L} = g(u, v) + \sum_i \mu_i(Eu - e)_i + \sum_i \nu_i (Fv - f)_i $$

where [math]\displaystyle{ g }[/math] is the argument from the minmax statement above and [math]\displaystyle{ u, v \geq 0 }[/math] become KKT conditions. The general update rule for Newton's method may be written in terms of the derivatives of [math]\displaystyle{ \mathcal{L} }[/math] with respect to primal variables [math]\displaystyle{ u, v }[/math] and dual variables [math]\displaystyle{ \mu, \nu }[/math], yielding:

$$ \nabla_{u,v,\mu,\nu}^2 \mathcal{L} \cdot (\Delta u, \Delta v, \Delta \mu, \Delta \nu)^T= - \nabla_{u,v,\mu,\nu} \mathcal{L} $$ where [math]\displaystyle{ \nabla_{u,v,\mu,\nu}^2 \mathcal{L} }[/math] is the Hessian of the Lagrangian and [math]\displaystyle{ \nabla_{u,v,\mu,\nu} \mathcal{L} }[/math] is simply a column vector of the KKT stationarity conditions. Combined with the previous section, this completes the goal of the paper: To construct a differentiable problem for learning normal form and extensive form games.

Experiments

We want to learn extensive form games in the presence of side information, with partial observations. To do this, we had three experiments. In all cases, we want to maximize the likelihood of realizing observed sequence from the player, assuming he acts in accordance to the QRE.

In the first experiment, we learn a non-symmetric variant of Rock, Paper, Scissors with side information. We consider the variant with the following payoff matrix: [Figure 2] where each of the [math]\displaystyle{ b }[/math] ’s are linear function of some features [math]\displaystyle{ x \in \mathbb{R}^{2} }[/math] (i.e., [math]\displaystyle{ b_y = x^Tw_y }[/math], [math]\displaystyle{ y \in {1,2,3} }[/math], where [math]\displaystyle{ w_y }[/math] are unknown). Features in the dataset [math]\displaystyle{ x }[/math]’s are drawn uniformly from [0, 1] and ground-truth weights [math]\displaystyle{ w_y }[/math]’s are drawn uniformly from [0, 10]. With a fixed test set of size 2000, we have the following results: [Figure 3]. From the graphs above, we can tell 1) both parameters learned and predicted strategies improve with larger dataset; and 2) with a reasonably sized dataset, >1000 here, convergence is stable and is fairly quick.

We investigate extensive form games with One-Card Poker introduced in EFG section. With assumption that the deck of size [math]\displaystyle{ n }[/math] is stacked uniformly, even the simple one-card poker is difficult to solve optimally since the normal form has [math]\displaystyle{ 2^{2n} }[/math] pure strategies for each player. However, in sequence form, we only need to work with realization plans of size [math]\displaystyle{ 4n }[/math]. In our experiment setup, we assume the deck is stacked non-uniformly. We want to learn this distribution of cards from observations of many rounds of the play. In this case, we need to know the player’s perceived or believed distribution of cards may be different from the distribution of cards dealt. Three experiments were run with [math]\displaystyle{ n=4 }[/math]. Each experiment comprises 5 runs of training, with same weights but different training sets. Let [math]\displaystyle{ d \in \mathbb{R}^{n}, d \ge 0, \sum_{i} d_i = 1 }[/math] be the weights of the cards. The probability that the players are dealt cards [math]\displaystyle{ (i,j) }[/math] is [math]\displaystyle{ \frac{d_i d_j}{1-d_i} }[/math]. This distribution is asymmetric between players. Matrix [math]\displaystyle{ P, E, F }[/math] for the case [math]\displaystyle{ n=4 }[/math] are presented in [1]. With training for 2500 epochs, the mean squared error of learned parameters (card weights, [math]\displaystyle{ u, v }[/math] ) are averaged over all runs of and are presented as following: [Figure 4]

From Security Resource Allocation Game, we demonstrate the ability to learn from incomplete observations. The defender possesses [math]\displaystyle{ k }[/math] indistinguishable and indivisible defensive resources which he splits among [math]\displaystyle{ n }[/math] targets, { [math]\displaystyle{ T_1, ……, T_n }[/math]}. The attacker chooses one target. If the attack success, attacker get [math]\displaystyle{ R_i }[/math] reward and defender get [math]\displaystyle{ -R_i }[/math], otherwise zero payoff for both. If there are n defenders guarding [math]\displaystyle{ T_i }[/math], probability of successful attack on [math]\displaystyle{ T_i }[/math] is [math]\displaystyle{ \frac{1}{2^n} }[/math]. Here’s the expected payoff matrix of when [math]\displaystyle{ n = 2, k = 3 }[/math], where the attackers are the row players. [Figure 5] For a multi-stage game where the attacker can launch [math]\displaystyle{ t }[/math] attacks, one in each stage while defender can only stick with stage 1. The attacker may change target if the attack in stage 1 is failed. Three experiments are run with [math]\displaystyle{ n = 2, k = 5 }[/math] for games with single attack and double attack, i.e, [math]\displaystyle{ t = 1 }[/math] and [math]\displaystyle{ t = 2 }[/math]. Each experiment is run 10 times for at least 2000 epochs per run. The mean and standard error over each run is showing below [Figure 6] We learn [math]\displaystyle{ R_i }[/math] only based on observations of the defender’s actions and our algorithm can still recover the game setting by only observing defender’s actions.

Same as expectation, the larger dataset size improves the learned parameters. Two outliers are 1) Security Game, the green plot for when [math]\displaystyle{ t = 2 }[/math]; and 2) RPS, when comparing between training sizes of 2000 and 5000.

References

[1] Ling, C. K., Fang, F., & Kolter, J. Z. (2018). What game are we playing? end-to-end learning in normal and extensive form games. arXiv preprint arXiv:1805.02777.

[2] B. von Stengel. Efficient computation of behavior strategies.Games and Economics Behavior,14(0050):220–246, 1996.

[3] Boyd, S., Boyd, S. P., & Vandenberghe, L. (2004). Convex optimization. Cambridge university press.