orthogonal gradient descent for continual learning: Difference between revisions
No edit summary |
No edit summary |
||
| Line 21: | Line 21: | ||
[[File:C--Users-p2torabi-Desktop-OGD.png]] | [[File:C--Users-p2torabi-Desktop-OGD.png]] | ||
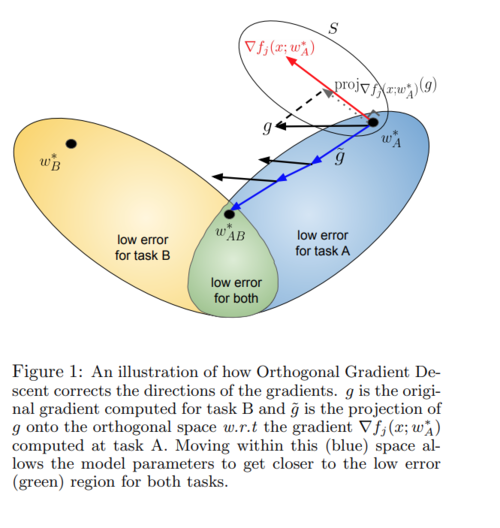
And perhaps the easiest way to understand this is pictorially. Here, Task A is the previously learned task and task B is the incoming task. The neural network f is indexed by j to show the jth logit. | |||
[[File:Pictoral_OGD.PNG|500px]] | |||
Revision as of 02:05, 14 November 2020
Authors
Mehrdad Farajtabar, Navid Azizan, Alex Mott, Ang Li
Introduction
Neural Networks suffer from catastrophic forgetting: forgetting previously learned tasks when trained to do new ones. Most neural networks can’t learn tasks sequentially despite having capacity to learn them simultaneously. For example, training a CNN to look at only one label of CIFAR10 at a time results in poor performance for the initially trained labels (catastrophic forgetting). But that same CNN will perform really well if all the labels are trained simultaneously (as is standard). The ability to learn tasks sequentially is called continual learning, and it is crucially important for real world applications of machine learning. For example, a medical imaging classifier might be able to classify a set of base diseases very well, but its utility is limited if it cannot be adapted to learn novel diseases - like local/rare/or new diseases (like Covid-19).
This work introduces a new learning algorithm called Orthogonal Gradient Descent (OGD) that replaces Stochastic Gradient Descent (SGD). In standard SGD, the optimization takes no care to retain performance on any previously learned tasks, which works well when the task is presented all at once and iid. However, in a continual learning setting, when tasks/labels are presented sequentially, SGD does not perform well - as will be shown in the results. OGD considers previously learned tasks by maintaining a space of previous gradients, such that incoming gradients can be projected onto an orthogonal basis of that space - minimally impacting previously attained performance.
Previous Work
Previous work in continual learning can be summarized into three broad categories. There are expansion based techniques, which add neurons/modules to an existing model to accommodate incoming tasks while leveraging previously learned representations. One of the downsides of this method is the growing size of the model with increasing number of tasks. There are also regularization based methods, which constraints weight updates according to some importance measure for previous tasks. Finally, there are the repetition based methods. These models attempt to artificially interlace data from previous tasks into the training scheme of incoming tasks, mimicking traditional simultaneous learning. This can be done by using memory modules or generative networks.
Orthogonal Gradient Descent
A gradient step moves the network towards the locally largest reduction (or increase) in loss. Similarly, a small step orthogonal to the gradient should result in no change to the loss. In order to learn new things without forgetting old ones, OGD proposes the intuitive notion of projecting newly found gradients onto an orthogonal basis of previously optimal gradients. Such an orthogonal basis will exist because neural networks are typically overparameterized, meaning they have more parameters than data points.
More specifically, OGD keeps track of the gradient with respect to each logit (OGD-ALL), since the idea is to project new gradients onto a space which minimally impacts the previous task across all logits. However, they have also done experiments where they only keep track of the gradient with respect to the ground truth logit (ODG-GTL) and with the logits averaged (OGD-AVE). OGD-ALL keeps track of gradients of dimension N*C where N is the size of the previous task and C is the number of classes. OGD-AVE and OGD-GTL only store gradients of dimension N since the class logits are either averaged or ignored respectively. To further manage memory, the authors sample from all the gradients of the old task, and they find that 200 is sufficient - with diminishing returns when using more.
The orthogonal basis for the span of previously attained gradients can be obtained using a simple Gram-Schmidt (or more numerically stable equivalent) iterative method.
Algorithm 1 shows the precise algorithm for OGD.
And perhaps the easiest way to understand this is pictorially. Here, Task A is the previously learned task and task B is the incoming task. The neural network f is indexed by j to show the jth logit.
Conclusion
Critiques
ada
References
[1] First Reference