XGBoost: A Scalable Tree Boosting System

Presented by

• Qianying Zhao
• Hui Huang
• Lingyun Yi
• Jiayue Zhang
• Siao Chen
• Rongrong Su
• Gezhou Zhang
• Meiyu Zhou

2 Tree Boosting In A Nutshell

2.1 Regularized Learning Objective

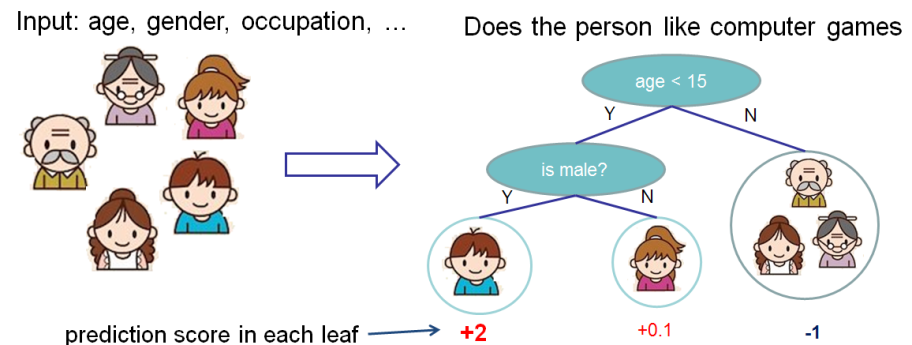
1. Regression Decision Tree (also known as classification and regression tree):

• Decision rules are the same as in decision tree
• Contains one score in each leaf value

2. Model and Parameter

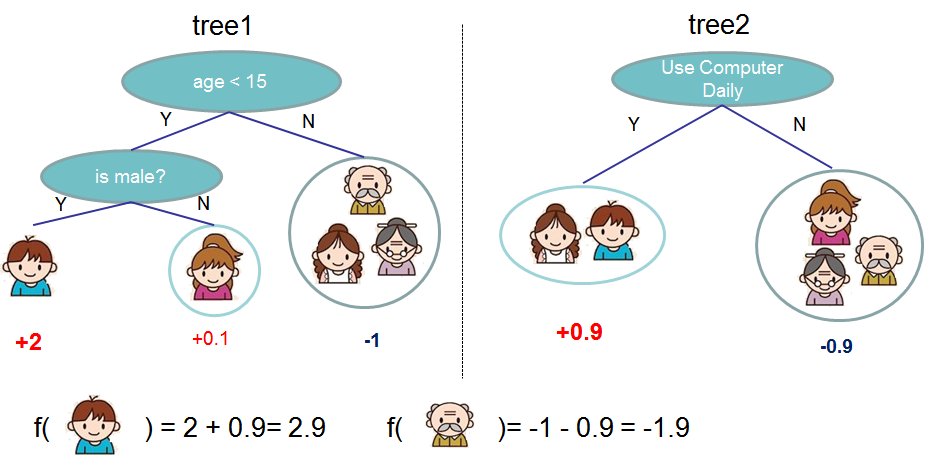
Model: Assuming there are K trees [math]\displaystyle{ \hat y_i = \sum^K_{k=1} f_k(x_I), f_k \in Ƒ }[/math]

Object: [math]\displaystyle{ Obj = \sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k) }[/math]

where [math]\displaystyle{ \sum^n_{i=1}l(y_i,\hat y_i) }[/math] is training loss, [math]\displaystyle{ \sum_{k=1}^K \omega(f_k) }[/math] is complexity of Trees

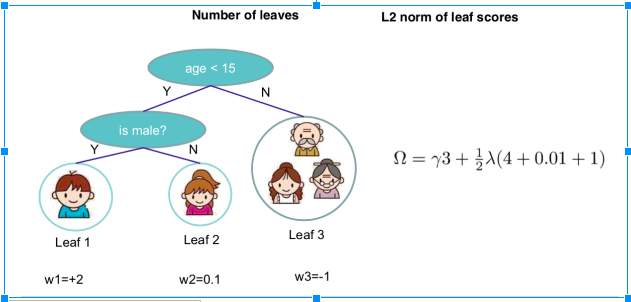
So the target function that needed to optimize is:[math]\displaystyle{ \sum_{i=1}^n l(y_i,\hat y_i)+\sum^K_{k=1}\omega(f_k), f_k \in Ƒ }[/math], where [math]\displaystyle{ \omega(f) = \gamma T+\frac{1}{2}\lambda||w||^2 }[/math]

For example:

Let's look at [math]\displaystyle{ \hat y_i }[/math]

[math]\displaystyle{ \hat y{i}^{(0)} = 0 }[/math]

[math]\displaystyle{ \hat y{i}^{(1)} = f_1(x_i)=\hat y_i^{(0)}+f_1(x_i) }[/math]

[math]\displaystyle{ \hat y{i}^{(2)} = f_1(x_i) + f_2(x_i)=\hat y_i^{(1)}+f_2(x_i) }[/math]

...

[math]\displaystyle{ \hat y{i}^{(t)} = \sum^t_{i=1}f_k(x_i)=\hat y_i^{(t-1)}+f_t(x_i) }[/math]

So [math]\displaystyle{ Obj^{(t)} = \sum_{i=1}^n l(y_i,\hat y_i^{(t)})+\sum^t_{i=1}\omega(f_i) }[/math]

                              =[math]\displaystyle{ \sum_{i=1}^n l(y_i,\hat y_i^{(t-1)}+f_t(x_i))+omega(f_t)+constant }[/math]

Take Taylor Expansion of the objective

[math]\displaystyle{ f(x+\delta x) \simeq f(x)+f^'(x)\deltax+\frac{1}{2}f^{''}(x)\delta x^2 }[/math]

then

[math]\displaystyle{ Obj^{(t)} = \sum^n_{i=1}[l(y_i,\hat y_i^{(t-1)})+g_if_t(x_i)+\frac{1}{2}h_i(x_i)]+\omega(f_t)+constant }[/math]

where [math]\displaystyle{ g_i =ə_{(\hat y_i)^{t-1}}(\hat y_i^{(t-1)}-y_i)^2 = d(\hat y_i^{(t-1)}-y_i)h_i = ə^2_{\hat y_i}^{(t-1)}(\hat y_i^{t-1)}-y_i)^2 =2 }[/math]

Define [math]\displaystyle{ I_j={i|q(x_i)=j} }[/math] as the instance set of leaf j and [math]\displaystyle{ f_t(x_i)=w_j }[/math]. We can rewrite target function as follows

[math]\displaystyle{ Obj^{(t)} = \sum^T_{j=1}[(\sum_{i\in I_j}g_i)wj+\frac{1}{2}(\sum_{i\in I_j h_i + \lambda)w_j^2]+\gamma T }[/math]

The optimal weight [math]\displaystyle{ w^*_j }[/math] of node j is [math]\displaystyle{ w_j^*=\frac{\sum_{i\in I_j}g_i}{\sum_{i\in I_j}h_i+\lambda} }[/math]

The loss reduction after the split is given by

[math]\displaystyle{ Obj_{split}=\frac{1}{2}[\frac{(\sum_{i \in I_l} g_i)^2}{\sum_{i \in I_l} h_i+\lambda}+\frac{(\sum_{i \in I_R} g_i)^2}{\sum_{i \in I_R} h_i+\lambda}-\frac{(\sum_{i \in I} g_i)^2}{\sum_{i \in I} h_i+\lambda}]-\lambda }[/math]