Wasserstein Auto-encoders

Introduction

Early successes in the field of representation learning were based on supervised approaches, which used large labelled datasets to achieve impressive results. On the other hand, popular unsupervised generative modeling methods mainly consisted of probabilistic approaches focusing on low dimensional data. In recent years, there have been models proposed which try to combine these two approaches. One such popular method is called variational auto-encoders (VAEs). VAEs are theoretically elegant but have a major drawback of generating blurry sample images when used for modeling natural images. In comparison, generative adversarial networks (GANs) produce much sharper sample images but have their own list of problems which include lack of encoder, harder to train, and "mode collapse" problem. Mode collpase problem refers to the inability of the model to capture all the variability in the true data distribution. Currently, there has been a lot of activity around finding and evaluating numerous GANs architectures and combining VAEs and GANs but a model which combines the best of both GANs and VAEs is yet to be discovered.

The work done in this paper builds up on the theoretical work done in [4]. The authors tackle generative modeling using optimal transport (OT). The OT cost is defined as measure of distance between probability distributions. One of the feature of OT cost which is beneficial is that it provides much weaker topology when compared to other costs including f-divergences which are associated with the original GAN algorithms. The problem with stronger notions of distances such f-divergences is that they often max out and provide no useful gradients for training. In comparison, the OT cost has been claimed to behave much more nicely [5, 8]. Despite the preceding claim, the implementation, which is similar to GANs, still requires addition of a constraint or a regularization term into the the objective function.

Original Contributions

Let [math]\displaystyle{ P_X }[/math] be the true but unknown data distribution, [math]\displaystyle{ P_G }[/math] be the latent variable model specified by the prior distribution [math]\displaystyle{ P_Z }[/math] of latent codes [math]\displaystyle{ Z \in \mathcal{Z} }[/math] and the generative model [math]\displaystyle{ P_G(X|Z) }[/math] of the data points [math]\displaystyle{ X \in \mathcal{X} }[/math] given [math]\displaystyle{ Z }[/math]. The goal in this paper is to minimize [math]\displaystyle{ OT\ W_c(P_X, P_G) }[/math].

The main contributions are given below:

• A new class of auto-encoders called Wasserstein Auto-Encoders (WAE). WAEs minimize the optimal transport [math]\displaystyle{ W_c(P_X, P_G) }[/math] for any cost function [math]\displaystyle{ c }[/math]. As is the case with VAEs, WAE objective function is also made up of two terms: the c-reconstruction cost and a regularizer term [math]\displaystyle{ \mathcal{D}_Z(P_Z, Q_Z) }[/math] which penalizes the discrepancy between two distributions in [math]\displaystyle{ \mathcal{Z}: P_Z\ and\ Q_Z }[/math]. [math]\displaystyle{ Q_Z }[/math] is a distribution of encoded points, i.e. [math]\displaystyle{ Q_Z := \mathbb{E}_{P_X}[Q(Z|X)] }[/math]. Note that when [math]\displaystyle{ c }[/math] is the squared cost and the regularizer term is the GAN objective, WAE is equivalent to the adversarial auto-encoders described in [2].

• Experimental results of using WAE on MNIST and CelebA datasets with squared cost [math]\displaystyle{ c(x, y) = ||x - y||_2^2 }[/math]. The results of these experiments show that WAEs have the good features of VAEs such as stable training, encoder-decoder architecture, and a nice latent manifold structure while simultaneously improving the quality of the generated samples.

• Two different regularizers. One based on GANs and adversarial training in the latent space [math]\displaystyle{ \mathcal{Z} }[/math]. The other one is based on something called "Maximum Mean Discrepancy" which known to have high performance when matching high dimensional standard normal distributions. The second regularizer also makes the problem fully adversary-free min-min optimization problem.

• The final contribution is the mathematical analysis used to derive the WAE objective function. In particular, the mathematical analysis shows that in the case of generative models, the primal form of [math]\displaystyle{ W_c(P_X, P_G) }[/math] is equivalent to a problem which deals with the optimization of a probabilistic encoder [math]\displaystyle{ Q(Z|X) }[/math]

Proposed Method

The method proposed by the authors uses a novel auto-encoder architecture to minimize the optimal transport cost [math]\displaystyle{ W_c(P_X, P_G) }[/math]. In the optimization problem that follows, the decoder tries to accurately reconstruct the data points as measured by the cost function [math]\displaystyle{ c }[/math]. The encoder tries to achieve the following two conflicting goals at the same time: (1) try to match the distribution of the encoded data points [math]\displaystyle{ Q_Z := \mathbb{E}_{P_X}[Q(Z|X)] }[/math] to the prior distribution [math]\displaystyle{ P_Z }[/math] as measured by the divergence [math]\displaystyle{ \mathcal{D}_Z(P_Z, Q_Z) }[/math] and, (2) make sure that the latent space vectors encoded contain enough information so that the reconstruction of the data points are of high quality. The figure below illustrates this:

Figure 1

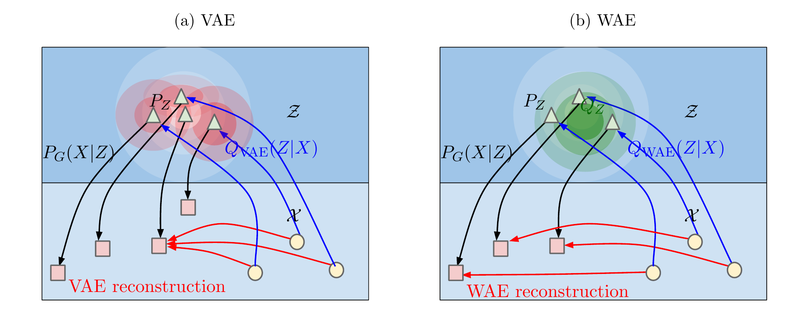
Figure 1: Both VAE and WAE have objectives which are composed of two terms. The two terms are the reconstruction cost and the regularizer term which penalizes the divergence between [math]\displaystyle{ P_Z }[/math] and [math]\displaystyle{ Q_Z }[/math]. VAE forces [math]\displaystyle{ Q(Z|X = x) }[/math] to match [math]\displaystyle{ P_Z }[/math] for the the different training examples drawn from [math]\displaystyle{ P_X }[/math]. As shown in the figure above, every red ball representing [math]\displaystyle{ Q_z }[/math] is forced to match [math]\displaystyle{ P_Z }[/math] depicted as whitish triangles. This causes intersection among red balls and results in reconstruction problems. On the other hand, WAE coerces the mixture [math]\displaystyle{ Q_Z := \int{Q(Z|X)\ dP_X} }[/math] to match [math]\displaystyle{ P_Z }[/math] as shown in the figure above. This provides a better chance of the encoded latent codes to have more distance between them. As a consequence of this, higher reconstruction quality is achieved.

Preliminaries and Notations

Authors use calligraphic letters to denote sets (for example, [math]\displaystyle{ \mathcal{X} }[/math]), capital letters for random variables (for example, [math]\displaystyle{ X }[/math]), and lower case letters for the values (for example, [math]\displaystyle{ x }[/math]). Probability distributions are are also denoted with capital letters (for example, [math]\displaystyle{ P(X) }[/math]) and the corresponding densities are denoted with lowercase letter (for example, [math]\displaystyle{ p(x) }[/math]).

Several measure of difference between probability distributions are also used by the authors. These include f-divergences given by [math]\displaystyle{ D_f(p_X||p_G) := \int{f(\frac{p_X(x)}{p_G(x)})p_G(x)}dx\ \text{where}\ f:(0, \inf) → \mathcal{R} }[/math] is any convex function satisfying [math]\displaystyle{ f(1) = 0 }[/math]. Other divergences used include KL divergence ([math]\displaystyle{ D_{KL} }[/math]) and Jensen-Shannon ([math]\displaystyle{ D_{JS} }[/math]) divergences.

Optimal Transport and its Dual Formations

A rich class of measure of distances between probability distributions is motivated by the optimal transport problem. One such formulation of the optimal transport problem is the Kantovorich's formulation given by:

[math]\displaystyle{ W_c(P_X, P_G) := \underset{\Gamma \in P(X \sim P_X ,Y \sim P_G)}{inf} \mathbb{E}_{(X,Y) \sim \Gamma}[c(X,Y)], \text{where} \ c(x, y): \mathcal{X} \times \mathcal{X} → \mathcal{R_{+}} }[/math]

is any measurable cost function and [math]\displaystyle{ \mathcal{P}(X \sim P_X, Y \sim P_G) }[/math] is a set of all joint distributions of (X, Y) with marginals [math]\displaystyle{ P_X\ \text{and}\ P_G }[/math] respectively.

A particularly interesting case is when [math]\displaystyle{ (\mathcal{X}, d) }[/math] is metric space and [math]\displaystyle{ c(x, y) = d^p(x, y)\ \text{for}\ p ≥ 1 }[/math]. In this case [math]\displaystyle{ W_p\lt /math, the \lt math\gt p-th }[/math] root of [math]\displaystyle{ W_c }[/math], is called the p-Wasserstein distance.

References

[1] D. P. Kingma and M. Welling. Auto-encoding variational Bayes. In ICLR, 2014.

[2] A. Makhzani, J. Shlens, N. Jaitly, and I. Goodfellow. Adversarial autoencoders. In ICLR, 2016.

[3] Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial nets. In NIPS, pages 2672–2680, 2014.

[4] O. Bousquet, S. Gelly, I. Tolstikhin, C. J. Simon-Gabriel, and B. Schölkopf. From optimal transport to generative modeling: the VEGAN cookbook, 2017.

[5] M. Arjovsky, S. Chintala, and L. Bottou. Wasserstein GAN, 2017.

[6] C. Villani. Topics in Optimal Transportation. AMS Graduate Studies in Mathematics, 2003.

[7] Sebastian Nowozin, Botond Cseke, and Ryota Tomioka. f-GAN: Training generative neural samplers using variational divergence minimization. In NIPS, 2016.

[8] I. Gulrajani, F. Ahmed, M. Arjovsky, V. Domoulin, and A. Courville. Improved training of wasserstein GANs, 2017.

[9] A. Gretton, K. M. Borgwardt, M. J. Rasch, B. Schölkopf, and A. J. Smola. A kernel two-sample test. Journal of Machine Learning Research, 13:723–773, 2012.

[10] F. Liese and K.-J. Miescke. Statistical Decision Theory. Springer, 2008.

[11] L. Mescheder, S. Nowozin, and A. Geiger. Adversarial variational bayes: Unifying variational autoencoders and generative adversarial networks, 2017.

[12] Y. Bengio, A. Courville, and P. Vincent. Representation learning: A review and new perspectives. Pattern Analysis and Machine Intelligence, 35, 2013.

[13] M. D. Hoffman and M. Johnson. Elbo surgery: yet another way to carve up the variational evidence lower bound. In NIPS Workshop on Advances in Approximate Bayesian Inference, 2016.

[14] S. Zhao, J. Song, and S. Ermon. InfoVAE: Information maximizing variational autoencoders, 2017.

[15] A. Genevay, M. Cuturi, G. Peyré, and F. R. Bach. Stochastic optimization for large-scale optimal transport. In Advances in Neural Information Processing Systems, pages 3432–3440, 2016.

[16] M. Cuturi. Sinkhorn distances: Lightspeed computation of optimal transport. In Advances in Neural Information Processing Systems, pages 2292–2300, 2013.

[17] Lenaic Chizat, Gabriel Peyré, Bernhard Schmitzer, and François-Xavier Vialard. Unbalanced optimal transport: geometry and kantorovich formulation. arXiv preprint arXiv:1508.05216, 2015.

[18] Matthias Liero, Alexander Mielke, and Giuseppe Savaré. Optimal entropy-transport problems and a new hellinger-kantorovich distance between positive measures. arXiv preprint arXiv:1508.07941, 2015.

[19] J. Zhao, M. Mathieu, and Y. LeCun. Energy-based generative adversarial network. In ICLR, 2017.

[20] V. Dumoulin, I. Belghazi, B. Poole, A. Lamb, M. Arjovsky, O. Mastropietro, and A. Courville. Adversarially learned inference. In ICLR, 2017.

[21] D. Ulyanov, A. Vedaldi, and V. Lempitsky. It takes (only) two: Adversarial generator-encoder networks, 2017.

[22] D. Berthelot, T. Schumm, and L. Metz. Began: Boundary equilibrium generative adversarial networks, 2017.

[23] Y. Li, K. Swersky, and R. Zemel. Generative moment matching networks. In ICML, 2015.

[24] G. K. Dziugaite, D. M. Roy, and Z. Ghahramani. Training generative neural networks via maximum mean discrepancy optimization. In UAI, 2015.

[25] R. Reddi, A. Ramdas, A. Singh, B. Poczos, and L. Wasserman. On the high-dimensional power of a linear-time two sample test under mean-shift alternatives. In AISTATS, 2015.

[26] C. L. Li, W. C. Chang, Y. Cheng, Y. Yang, and B. Poczos. Mmd gan: Towards deeper understanding of moment matching network, 2017.

[27] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. In Proceedings of the IEEE, volume 86(11), pages 2278–2324, 1998.

[28] Ziwei Liu, Ping Luo, Xiaogang Wang, and Xiaoou Tang. Deep learning face attributes in the wild. In Proceedings of International Conference on Computer Vision (ICCV), 2015.

[29] D. P. Kingma and J. Lei. Adam: A method for stochastic optimization, 2014.

[30] A. Radford, L. Metz, and S. Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. In ICLR, 2016.

[31] S. Ioffe and C. Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift, 2015.

[32] Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, Günter Klambauer, and Sepp Hochreiter. GANs trained by a two time-scale update rule converge to a nash equilibrium. arXiv preprint arXiv:1706.08500, 2017.

[33] B. Poole, A. Alemi, J. Sohl-Dickstein, and A. Angelova. Improved generator objectives for GANs, 2016.